1. Переменные величины: определение, хар-ка, ф-ия, элементы ф-ии (классификация, графики). Линейная ф-ия, дробно-линейная, квадратный трехчлен, показательная, логарифмическая, тригонометрическая, обратные тригонометрические ф-ии.

Все вел-ны в мат-ке дел-ся на 2 кл.: переем-е и пост-е. Пер-я-вел-ча, к-я принимает разл-е числ-е знач-я (x,y,z). Пост-я-в-на, числ-е зная-я к-й не меняются (a,b,c). Вел-на, к-я сохр-т свое знач-е в любом времени н-ся абсолютнопостоянной. Сов-ть всех числ-х знач-й перм-й вел-ны, н-ся областью изменения этой вел-ны: 1) интервал (a<x<b) x € (a,b) – сов-ть чисел х, заключ-х между данными числами а и b. 2) Отрезок (сегмера): a≤x≤ b; x € [a,b]…., включая эти числа (сов-ть всех точек х, закл-х между данными точками a и b (концами отрезка), к-е принадлежат рассматриваемой сов-ти). Окрестность т. х₀-произвольные интервалы (a,b), содержащие эту точку внутри себя, концы к-го удовлетворяют условию: a< х₀<b. ε-окрестность т. х₀-интервал (х₀-ε, х₀+ε), где х₀-центр окрестности, ε-радиус окрестности.

Хар-ки: 1) упорядоченная пер-я вел-на-пер-я вел-на х-упорядоченная переменная, если в обл-ти изменения пер-й вел-ны установлен порядок соотв-х ее зн-й; 2) возраст-я (убыв-я)-монотонные-пер-я вел-на н-ся возраст-й , елли каждое ее последующее знач-е больше пред-го; убыв-я-наоборот; 3) огранич-я пер-я вел-на-если можно указать такой отрезок [-M;M], что все последующие значения переменной, начиная с нек-го будут принадлежать этому отрезку.

Если каждому значению пер-й вел-ны х, принадлежащей нек-й обл-ти, соот-т значение др. пер-й вел-ны y, то говорят, что y-функция от х. y=f(x). ООФ-сов-ть знач-й пер-й х, для к-х опр-ся знач-е ф-ии y в силу правила f(x). Пер-я в-на х н-ся независимой или аргументом. Пер-я в-на y н-ся ф-й от пер-й вел-ны х. Зав-ть между х и y н-ся функц-ой зав-ю. С-ть знач-й пер-й y, соотв-я знач-м аргумента н-ся обл-ю изменения ф-ии y.

Если большему зн-ю агрумента х, взятому из ООФ, соотв-т большее зн-е ф-ии y=f(х), то ф-я н-ся возрат-й (х₂>х₁, f(x₂)>f(x₁)); х₂≥х₁, f(x₂)≥f(x₁) – невозраст-я. х₂>х₁, f(x₂)<f(x₁ – убыв-я. Способы зад-я ф-й: табличный, графич-й, аналитический, словестный.

Алгебраические

1) Степенная: y=x^a

2) Линейная ф-я: y=ax+b(y=ax, b=0; y=b, a=0).

3) Дробно-линейная: y=(ax+b)/(cx+d)=m+k/(x-n); x≠n, y≠m.

4) Квадратный трехчлен: y=ax²+bx+c. x_b=-b/2a. x=a₁y²+b₁y+c.

5) Кубич-я парабола (трехчлен) y=ax³

Неалгебраические

1) Показательная y=a^x, a>1, 0<a<1

2) Лог-я y=log_ax, a>1, 0<a<1

3

y

) Триг-е y=sinx; y=cosx; y=tgx;y=ctgx; y=1/sinx=cosecx; y=cosx=secx

x

y=1/cos x; cos x=sin(П/2 – х); sec x=cosec(П/2-х)

cos x ≠ 0; x ≠ П/2+Пn; Є Z; n=0, ±1, ±2, ….

x

cosec x

4) y=arcsinx, -1<x<1, -П/2<y<П/2; y=arccosx, -1<x<1, 0<y<П

y=arctgx, -∞<x<+∞, -П/2<y<П/2

y=arctgx, -∞<x<+∞, 0<y<П

2. Соотнощения между обратными тр-ми ф-ями

1) arcsin(-x)=–arcsinx; 2)arcos(–x)= П–arccosx; 3) arctg(-x)= –arctgx; 4) arcctg(-x)=П–arcctgx; 5) arcsinx+arccosx=П/2; 6) arctgx+arcctgx=П/2; 7) sin(arcsinx)=x, -1≤x≤1; 8) arcsin(sinx)=x, -П/2<x<П/2; 9) cos(arccosx)=x, -1≤x≤1; 10) arcos(cosx)=x, 0≤x≤П; 11) tg(arctgx)=x, –∞<x<+∞; 12) arctg(tgx)=x, -П/2<x<П/2; 13) ctg(arcctgx)=x, –∞<x<+∞; 13) arcctg(ctgx)=x, 0<x<П.

3. Преобразование графиков ф-ий

1) y=f(x+a); 2) y=f(x)+b; 3) y=f(-x); 4) y=-f(x); 5) y=f(|x|); 6) y=|f(x)|; 7) y=f(kx); 8) y=kf(x); 9) Сложение графиков ф-й.

4. Полярная система координат.

→

|OM|=ρ 0<ρ<∞ 0 – начало координал (полюс)

0+2П*n ≤ φ ≤ 2П + 2П*n n=0, ±1, 2±….

Связь междупрямоугольной и полярной системой координат

y=*cosφ; x=*sinφ; tgφ=y/x; =∞√(x²+y²); cosφ=y/(√(x²+y²); sinφ= x/(√(x²+y²); =a*cosφ; =sinφ.

√(x²+y²)=x/√(x²+y²)

x²+y²=x

x²-x+y²=0

x²-2*1/2*x+1/4-1/4+y²=0

(x-1/2)²+y²=1/4

C(1/2;0) R=1/2

5. Параметрически заданная ф-ия. Основные виды кривых в параметрической форме: эллипс, окружность, астероида, цикоида. Переход от параметрически заданного вида ф-ии к прямоугольной координатам.

Параметрическое задание ф-ии:

x=x(t)

y=y(t) t-промежуточный параметр

F(x,y)=0

От параметрического задания ф-ии можно перейти к заданию ф-ии в пр-х коор-х, исключая из данных равенств промежуточный параметр t.

{x=2cost

y=2sint

{x²=4cos²t

y²=4sin²t: x²=4cos²t + y²=4sin²t: x²+y²=4(cos²t+sin²t)

sin²t+cjs²t=1: x²+y²=1

x²+y²=R

1) Элипс

x

a > b

2 )Окр-ть

x

a = b

3) Остроида

4) Циклоида

{x=a (t – sin t)

{y=a (1– cos t) 0 ≤ t ≤ 2П

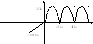
5) Кардиоида

ρ = a(1 + cosφ)

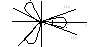
6) Трехлепестковая роза

ρ = a cos 3φ

6. Теория пределов. Определение пределов и их геометрическая интерпретация. Односторонние пределы для этих случаев.

1) lim f(x)=A

xa

Число А н-ся пределом ф-ии f(x) в точке а (или при ха), если для любого пол-го числа ε существует (найдется) такое полож-е число , зависящее от ε: (ε), что при всех х≠а и удовл-м условию |х-а|<, вып-ся условие |f(x)-A|<ε.

Геом-я интер-я

А-ε<f(x)< А+ε

lim f(x)=A

xa Означает, если для любого пол-го числа ε сущ-т пол-е число  такое, что как только х попадает в  окр-ть т. а, значение ф-ии f(x) попадает в ε-окр-ть т.А.

Если ха, оставаясь <а, то пишут: ха-0 (слева). Если ха, оставаясь >а, то пишут: ха+0 (справа). Говорят об односторонних пределах ф-ии:

lim f(x)=A

xa-0 : ε>0; (ε)>0; x≠a; a-<x<a вып-ся усл-е: |f(x)|<ε

lim f(x)=A

xa+0 ε>0; (ε)>0; x≠a; a<x<a+ вып-ся усл-е: |f(x)|<ε

2) lim f(x)=A

x∞ Предел ф-ии f(x), при х0 равен А, если по любому пол-му ε найдется такое число N, зависящее от , что для всех х удовлетв-х неравенству |x|>N вып-ся условие |f(x)-A|<ε

Геом-я интер-я

По любому пол-му ε найдется такое пол-е N, зависящее от ε, что как только знач-е х попадает в интервал х€(N;+∞); х€(-∞;N),то значение ф-ии f(x) попадает в ε-окр-ть т.А.

-ε<f(x)<ε

3) lim f(x)=∞

xa N>0 (N)>0 |x-a|< |f(x)|>N

Геом-я интер-я

4 ) lim f(x)=∞

x∞ Нулевому пол-му числу N>0 сущ-т M(N)>0, как только |x|>M, то |f(x)|>N

Геом-я интер-я

|x|>M: [x>M

x<-M

|f(x)|>N: [f(x)>N

f(x)<-N

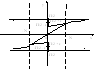
7. Теория о существовании предела ф-ии в точке x=A

limf(x)=A

xa

Чтобы сущ-л limf(x)=A в т. х=а необходимо и достаточно чтобы существовал левосторонний предел ф-ии в этой точке и они были бы равны между собой, т.е.

limf(x)= limf(x)=A  limf(x)

xa-0 xa+0 xa

8.Числовая последовательность. Определения, виды, поведение. Определение предела числовой последовательности. Геометрическая иллюстрация.

Числовой посл-ю н-ся сов-ть чисел, занумерованных в опр-м порядке. Чис-ю пос-ть можно представить как ф-ию целочисленного аргумента, т.е. каждому целочисленному значению ф-ии f(x)=f(n)=a_n; a=n. a_n – общий член числовой пос-ти. { a_n}: a₁, a₂, a₃,…, a_n

Чис-я посл-ть н-ся монотонновозрастающей, если каждый аоследующий ее член больше предыдущего. {n/(n+1)}

Ч-я п-ть н-ся монотонноубывающей, если каждый ее последующий член меньше предыдущего. {1/n}

Ограниченная ч-я п-ть: ч-я п-ть ограничена сверху, если существует такое число N, что для всех n вып-ся условие: a_n≤N. Ч-я п-ть ограничена снизу, если существует такое число M, что для всех n вып-ся условие: a_n≥M. Пр-р: {n/(n+1)} N=1 n/(n+1)<1 M=0 1/n>0.

Ч-я посл-ть н-ся ограниченной, если она ограничена сверху и снизу, т.е. сущ-т такое число р, что для любого n вып-ся условие: |a_n|≤p.

Ограниченные пос-ти имеют предел. Пос-ть, имеющая предел, н-ся сходящейся посл-ю.

А – на-ся пределом числовой пос-ти a_n, если длял любого ε>0 сущ-т такой номер члена, начиная с которого (или для всех n>N(ε)) вып-ся неравенство: |a_n-A|<ε.

Геометрическая интерпретация:

lim a_n =А

n∞

ε>0 N(ε)>0 (n>n(ε)) |a_n-A|<ε. Преобразуем |a_n-A|<ε

-ε< a_n-A<ε → A-ε< a_n<A+ε ε-окрестность т.А

Какую бы малую ε-окрестность т.А не взяли, все значения a_n, начиная с некоторого номера, должны попасть в эту окр-ть так, что вне ее может остаться конечное число этих значений (n).

9. Ограниченные ф-ии. Определения, примеры. Теорема о связи ограниченной и сходимости ф-ий к конечному пределу.

Ф-ия y=f(x) н-ся ограниченной в данной области изменения аргумента х, если существует такое положительное число М>0, что для всех х, принадлежащих рассматриваемой области, будет выполняться условие |f(x)|≤М.

1) y=sinx M=1 |sinx|≤1 -∞<x<+∞

2) y=cosx M=1 |cosx|≤1 -∞<x<+∞

1) Если такое число М не сущ-т, то ф-ия y=f(x) явл-ся неограниченной в области существования.

2) Ф-ия y=f(x) наз-ся ограниченной при х→а, если существует окрестность с центром в т. А, в которой данная ф-ия ограничена.

3) Ф-ия y=f(x) н-ся ограниченной при х→∞, если сущ-т такое число N>0, что при всех значениях х, удовлетворяющих условию |x|>N, ф-ия f(x) ограничена.

Теорема о связи между пределом функции и ее ограниченностью и сходимости ф-ий к конечному пределу.

Теорема: lim f(x)=A, при этом А – конечное число, то ф-ия

xa

f(x) явл-ся ограниченной при х→а.

Док-во: При док-ве этой теоремы используются св-ва действительных чисел: |x+y|≤|x|+|y| |x-y|≥|x|-|y|

Дано: lim f(x)=A – конечное число.

xa

Док-ть: M>0, |f(x)|≤M.

lim f(x)=A – означает: ε>0 δ(ε)>0 |x-a|<δ |f(x)-A|<ε

xa

a-δ<x< a+δ δ-окрестность т.а, т.е. |f(x)-A|<ε выполняется для всех х из δ-окрестности т.а. Преобразуем неравенство |f(x)-A|<ε. Для этого выполняется свойство действительных чисел |x-y|≥|x|-|y| |f(x)-A|≥|f(x)|-|A|

Заменим в неравенстве |f(x)-A|<ε левую часть.

Получим: |f(x)|-|A|<ε или |f(x)|<|A|+ε, где |A|+ε=M>0.

Окончательно получим:

Для всех х из δ-окрестности т.а вып-ся условие: |f(x)|<M, где М=|A|+ε>0. Это означает, что ф-ия f(x) ограничана для всех x из δ-окрестности т.а.

Теорема 2: если lim f(x)=A≠0, то ф-ия 1/f(x) является

xa

ограниченной при xa.