2 lectures

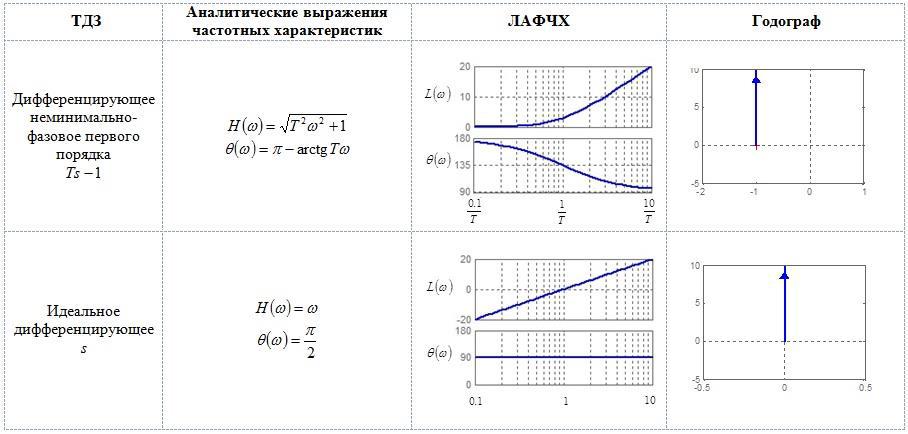
Рис. 3.7 (продолжение)

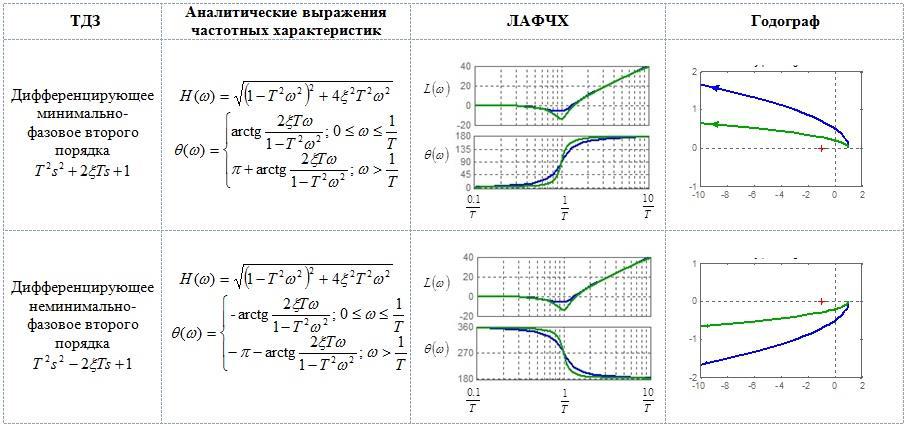
Рис. 3.7 (продолжение)

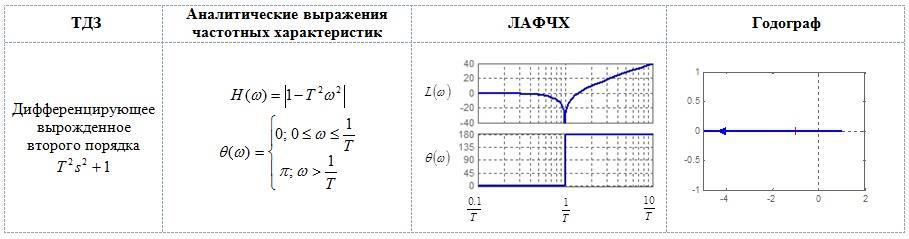
Рис. 3.7 (продолжение)

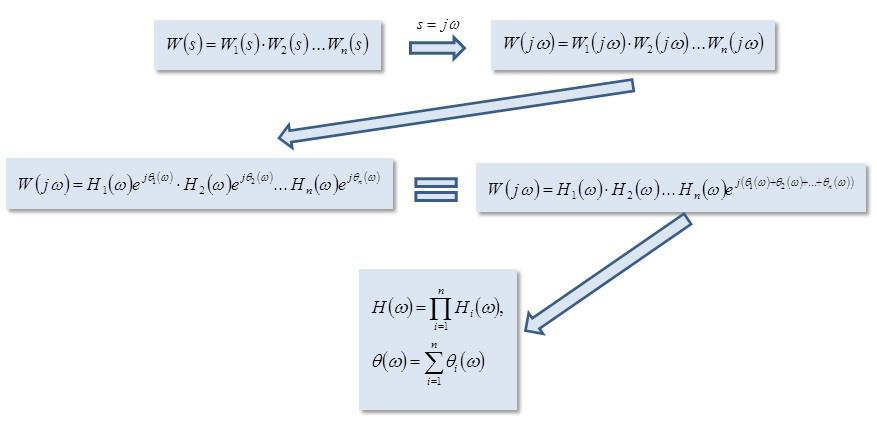
3.3.3 Построение частотных характеристик сложных систем

Следующий рисунок на примере демонстрирует алгоритм нахождения аналитических выражений амплитудной и фазовой частотной

характеристик сложной системы.

Рис. 3.8

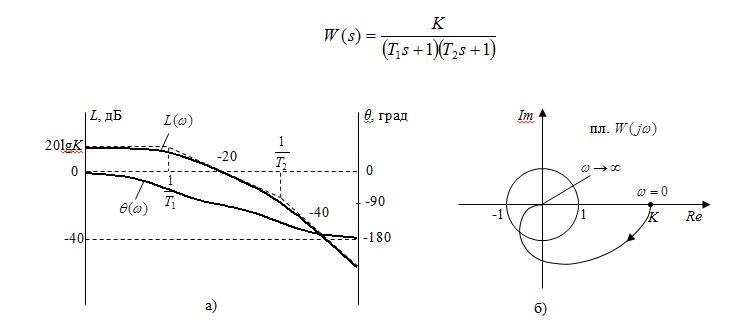
Для построения логарифмических частотных характеристик также можно воспользоваться таблицей типовых динамических звеньев.

Для этого удобно использовать метод разбиения передаточной функции на простые множители, что означает представление ее в виде произведения типовых динамических звеньев. Рассмотрим пример системы на рисунке 3.9, заданной в виде произведения двух апериодических звеньев.

Логарифмические амплитудную и фазовую частотные характеристики получают путем суммирования соответственно амплитуд и фаз типовых динамических звеньев (рисунок 3.9 а). Годограф можно легко построить по полученным ЛАФЧХ (рисунок 3.9 б).

Рис. 3.9

Презентация 4. Исследование устойчивости

4.1	Понятие устойчивости по Ляпунову ............................................................................................................................................................................	2
4.2	Прямой метод исследования устойчивости линейных систем..................................................................................................................................	4
4.3	Алгебраический критерий устойчивости Гурвица .....................................................................................................................................................	5
4.4	Критерий устойчивости Найквиста-Михайлова. Понятие запасов устойчивости ..................................................................................................	6

4.1 Понятие устойчивости по Ляпунову

Понятие устойчивости системы автоматического управления тесно связано с понятием устойчивости ее положения равновесия. Если говорить о линейной автономной (изолированной от внешних воздействий) системе, то ее положение равновесия всегда находится в нуле n-

мерного пространства переменных состояния.

Определение. Если траектория в n-мерном пространстве переменных состояния, начавшись в некоторой окрестности положения равновесия, с течением времени стремится к нему, то такое положение равновесия называется асимптотически устойчивым.

Соответствующая система называется асимптотически устойчивой.

Определение. Если траектория в n-мерном пространстве переменных состояния, начавшись в некоторой окрестности положения равновесия, с течением времени удаляется от него, то такое положение равновесия называется неустойчивым. Соответствующая система называется неустойчивой.

Определение. Если траектория в n-мерном пространстве переменных состояния, начавшись в некоторой окрестности положения равновесия, с течением времени не стремится и не удаляется от него, то такое положение равновесия называется устойчивым.

Соответствующая система называется устойчивой.

Для системы второго порядка n-мерное пространство переменных состояния сводится к так называемой фазовой плоскости, где по оси абсцисс откладывается первая координата вектора состояния x1, в качестве которой выбираем выходной сигнал, а по оси ординат вторая координата x2 в виде ее скорости изменения.

Общее решение уравнений состояния задает на фазовой плоскости фазовую траекторию, параметром вдоль которой является время.

На рисунке 4.1 показаны четыре примера систем: неустойчивой (а), асимптотически устойчивой (в) и устойчивой (б, г).

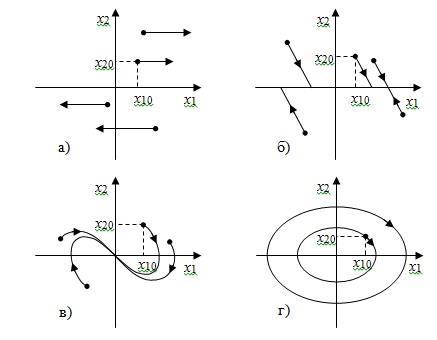
Рис. 4.1

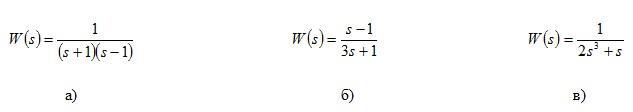
4.2 Прямой метод исследования устойчивости линейных систем

Об устойчивости можно судить по расположению полюсов (корней полинома знаменателя передаточной функции) системы на

комплексной плоскости.

Если все полюса передаточной функции расположены в левой части комплексной плоскости, то соответствующая система является асимптотически устойчивой

Если среди всех полюсов передаточной функции есть хоть один полюс, расположенный в правой части комплексной плоскости, то соответствующая система является неустойчивой

Если помимо полюсов передаточной функции, располагаемых в левой части комплексной плоскости, есть один или несколько некратных полюсов на мнимой оси, то такая система является устойчивой.

На рисунке 4.2 приведены примеры неустойчивой (а), асимптотически устойчивой (б) и устойчивой (в) систем.

Рис. 4.2

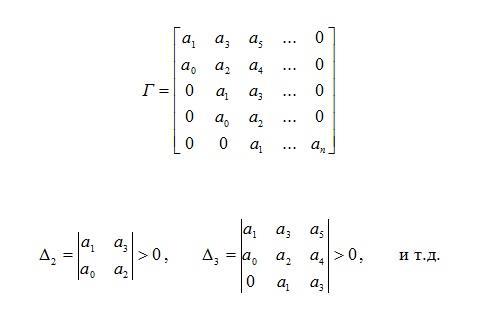
4.3 Алгебраический критерий устойчивости Гурвица

Критерий Гурвица работает с коэффициентами характеристического уравнения системы.

Определение. Характеристическим уравнением называется полином знаменателя передаточной функции, приравненный нулю.

Пусть характеристическое уравнение некоторой исследуемой системы имеет вид:

a0 sn a1sn 1 ... an 0.

Необходимым условием критерия является положительность всех коэффициентов характеристического уравнения.

Достаточным условием асимптотической устойчивости является положительность всех диагональных миноров так называемой матрицы Гурвица (рисунок 4.3).

Рис. 4.3