Вопрос 29. Вероятность ошибочного приема кодовой информации для простого двоичного кода и для кода с исправлением ошибок кратности t.
Для двоичного симметричного канала передачи вероятность ошибочного приема любых l символов в n-элементной кодовой комбинации подчиняется биномиальному закону распределения
Pn(l)=Cnlpl(1-p)n-l.
Неправильный прием одного, двух, и т.д. элементов из n-элементной кодовой комбинации обозначают термином «одиночная», «двойная» и т. д. ошибка соответственно. Или говорят, что произошла ошибка кратности l.
Если код исправляет ошибки кратности t, то вероятность ошибочного приема кодовой комбинации равна
.
(4.4)
Пусть исправляется ошибка кратности t=1. Тогда из (4.4) для рассмотренного выше примера (где n=8) получим:
РК=8*10-3 – 8*10-3*0.9997)≈5.6*10-5.
Исправление всего лишь однократной ошибки повышает помехоустойчивость избыточного кода на два порядка.
Вопрос 30. Простейшие избыточные коды.
ПРОСТЕЙШИЕ ИЗБЫТОЧНЫЕ КОДЫ
Код с четным числом единиц. Код с четным числом единиц образуется из исходного k-элементного кода добавлением еще одного элемента, нуля или единицы, таким образом, чтобы количество единиц в новой кодовой комбинации было четным. Для определения дополнительного элемента все элементы исходной кодовой комбинации складывают по модулю 2:
0 1 1 1 0 1 1 0 = 1,
0 0 1 1 0 1 1 0 = 0.
Таким образом, число элементов в новой кодовой комбинации n=k+r=k+1. Избыточность кода с четным числом единиц
.
(4.5)
Этот код имеет кодовое расстояние d=2 и обнаруживает все нечетные ошибки.
Корреляционный код
При построении корреляционного кода каждый элемент исходного кода преобразуется в 2 элемента:
1 à 10,
0 à 01.
Таким образом, корреляционный код относится к непрерывным кодам.
Если исходная комбинация содержит k элементов, то новая кодовая комбинация – n=2k. Избыточность корреляционного кода R=0,5 .
Помехоустойчивость корреляционного кода обеспечивается тем, что появление необнаруживаемой ошибки возможно возможно только в случае, когда два рядом стоящих элемента, соответствующих одному элементу исходной кодовой комбинации будут одновременно искажены, то есть 1à0, а 0à1. Вероятность этого события
РНО=р2. В корреляционном коде в линию связи всегда передается одинаковое число 0 и 1, что обеспечивает эффективное использование ее пропускной способности.
Вопрос 31. Групповой код Хемминга. Принципы построения. Синдром ошибки. Коды с обнаружением и исправлением ошибок. Код хемминга
Код Хемминга относится к блоковым кодам. Наиболее простой код, исправляющий ошибки кратности t=1, имеет кодовое расстояние d=3.
Принцип построения:
1) На передающей стороне к k информационным символам добавляется r проверочных символов. Значения проверочных символов (0 или 1) определяются путем проверок на четность. В проверку на четность включают определенные элементы кодовых комбинаций, образующие проверочную группу. Сформированный n-разрядный код, состоящий из k информационных и r проверочных элементов, передается в линию связи.
2) На приемной стороне в тех же проверочных группах производится r проверок на четность.
3)
Проверочные группы строятся таким
образом, чтобы записи результатов каждой
проверки
в двоичной форме давало бы r-разрядное
двоичное число
,
указывающее номер разряда (в исчислении
с основанием 10) искаженного элемента.
Это выражение называют синдромом
ошибки.
Для
того чтобы
обнаружить и исправить все ошибки
кратности 1, число проверочных символов
выбирается из соотношения
.
Добавление слагаемого +1 соответствует
случаю отсутствия ошибок.
Число элементов помехоустойчивой кодовой комбинации определяется из решения уравнения относительно n:
.
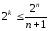(4.6)
Изначально известно число k. Определив n из уравнения (4.6), получим число проверочных разрядов r в новых кодовых комбинациях (таблица 4.1).
Таблица 4.1 – Соотношение числа информационных и проверочных разрядов
|
k |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
n |
5 |
6 |
7 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
17 |
|
r |
3 |
3 |
3 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
5 |