- •Вопрос 2.
- •Часть 1.Количественная мера информации для равновозможных событий
- •Часть 2. Мера р. Хартли
- •Вопрос 3.
- •Вопрос 4.
- •Вопрос 5.
- •Вопрос 6. Свойства энтропии источника дискретных сообщений
- •Вопрос 7. Энтропия источника совместных сообщений
- •Вопрос 8. Что такое условная энтропия?
- •Вопрос 9.
- •Вопрос 10. Свойства количественной меры информации при неполной достоверности результатов опыта.
- •Вопрос 11. Вычисление количественной меры информации для двоичного канала с помехами.
- •Вопрос 12. Как оценивается избыточность источника сообщений?
- •Вопрос 13.
- •Вопрос 23.
- •Вопрос 24. Приведите модель двоичного канала с шумами
- •Вопрос 25.
- •Вопрос26. Формула Шеннона для аналогового канала с шумами.
- •Вопрос 27. Энтропия источника при наличии коррелятивных связей между двумя соседними символами
- •Вопрос 28. Принципы помехоустойчивого кодирования. Кодовое расстояние.
- •Вопрос 29. Вероятность ошибочного приема кодовой информации для простого двоичного кода и для кода с исправлением ошибок кратности t.
- •Вопрос 30. Простейшие избыточные коды.
- •Вопрос 31. Групповой код Хемминга. Принципы построения. Синдром ошибки. Коды с обнаружением и исправлением ошибок. Код хемминга
- •Вопрос 32. Определение числа проверочных элементов.
- •Вопрос 33. Определение проверочных элементов, входящих в каждую группу. Исправляющая способность кода хемминга
Вопрос 13.
13. Укажите достоинства и недостатки избыточности сообщений.
Вспомним теперь, что энтропия характеризует количество информации, приходящееся в среднем на одно сообщение.
Энтропия источника
максимальна и равна
 ,
если символы вырабатываются с равными
вероятностями; если же это не так и
некоторые символы повторяются часто,
а другие редко, то энтропия источника
уменьшается, а при появлении дополнительных
коррелятивных связей между символами
энтропия становится еще меньшей. Это
положение хорошо согласуется с интуитивным
представлением о количестве информации,
вырабатываемой тем или иным источником.
Так, например, если из предшествовавшего
опыта свойства лектора или докладчика
известны настолько хорошо, что слушатели
с высокой степенью достоверности знают,
о чем он будет говорить, то количество
информации, сообщаемой таким лектором,
будет очень малым, несмотря на большое
количество произнесенных слов.
,
если символы вырабатываются с равными
вероятностями; если же это не так и
некоторые символы повторяются часто,
а другие редко, то энтропия источника
уменьшается, а при появлении дополнительных
коррелятивных связей между символами
энтропия становится еще меньшей. Это
положение хорошо согласуется с интуитивным
представлением о количестве информации,
вырабатываемой тем или иным источником.
Так, например, если из предшествовавшего
опыта свойства лектора или докладчика
известны настолько хорошо, что слушатели
с высокой степенью достоверности знают,
о чем он будет говорить, то количество
информации, сообщаемой таким лектором,
будет очень малым, несмотря на большое
количество произнесенных слов.
Для того чтобы выяснить, насколько хорошо в источнике сообщений используются разные символы (а источник будет тем лучше, чем больше информации он будет вырабатывать), вводится параметр, называемый избыточностью и равный
 .
(1.24)
.
(1.24)
При этом
 есть максимальная энтропия или наибольшее
количество информации, которое может
приходиться на один символ источника
при данном числе
есть максимальная энтропия или наибольшее
количество информации, которое может
приходиться на один символ источника
при данном числе
 используемых символов.
используемых символов.
Из (1.24) видно, что
при
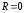 энтропия источника
энтропия источника ,
т.е. источник генерирует максимальное
количество информации на символ. Если
,
т.е. источник генерирует максимальное
количество информации на символ. Если
 ,
то
,
то
 и, следовательно, информация, вырабатываемая
источником, равна нулю. В общем случае
и, следовательно, информация, вырабатываемая
источником, равна нулю. В общем случае
 .
Чем меньше избыточность
.
Чем меньше избыточность
 ,
тем рациональнее работает источник,
тем большее количество информации он
вырабатывает.
,
тем рациональнее работает источник,
тем большее количество информации он
вырабатывает.
Следует, однако,
иметь в виду, что не всегда нужно
стремиться к тому, чтобы
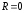 .
Некоторая избыточность бывает полезной
для обеспечения надежности передачи,
регистрации и других преобразований
информации. Известно, например, что
лектора, который не повторяет или не
разъясняет более подробно, на примерах
отдельные положения, слушать и
конспектировать значительно труднее,
чем лектора, который в разумной мере
пользуется этими приемами.
.
Некоторая избыточность бывает полезной
для обеспечения надежности передачи,
регистрации и других преобразований
информации. Известно, например, что
лектора, который не повторяет или не
разъясняет более подробно, на примерах
отдельные положения, слушать и
конспектировать значительно труднее,
чем лектора, который в разумной мере
пользуется этими приемами.
Если не различать буквы «е» и «ё», а также мягкий и твердый знаки, то в русском алфавите всего 31 буква, к ним нужно добавить еще пробел между словами, так что всего получается 32 символа. Если бы все символы были равновероятны, то энтропия такого языка была бы равна
 .
.
В действительности, однако, вероятности различных символов различны; так, например, вероятность буквы «о» равна приблизительно 0,09, а буквы «ф» – 0,002. Кроме того, между символами имеют место значительные коррелятивные связи.
Проведенные исследования дают следующие значения энтропии:
при учете разной вероятности отдельных символов
 ,
,
при учете коррелятивных связей между двумя символами
 ,
,
при учете коррелятивных связей между тремя символами
 .
.
Таким образом, можно утверждать, что избыточность русского языка
 .
.
Анализ английского
языка с учетом коррелятивных связей,
распространяющихся на восемь соседних
букв, показал, что избыточность его
 .
Если учесть коррелятивные связи,
распространяющиеся на достаточно
большое число букв, то можно, по-видимому,
убедиться что избыточность русского и
других европейских языков более 50.%.
Наличие этой избыточности позволяет
легко исправлять отдельные ошибки или
восстанавливать пропуски букв и даже
слогов без искажения текста.
.
Если учесть коррелятивные связи,
распространяющиеся на достаточно
большое число букв, то можно, по-видимому,
убедиться что избыточность русского и
других европейских языков более 50.%.
Наличие этой избыточности позволяет
легко исправлять отдельные ошибки или
восстанавливать пропуски букв и даже
слогов без искажения текста.
 помехоустойчивые
коды
помехоустойчивые
коды
Это избыточные коды в которых число разрешенных кодовых комбинаций меньше общего числа кодовых комбинаций, возможных для двоичного кода данной разрядности.
Что такое избыточность кода
Код с четным числом единиц образуется из исходного k-элементного кода добавлением еще одного элемента, нуля или единицы, таким образом, чтобы количество единиц в новой кодовой комбинации было четным.Избыточность кода можно оценить выражением: – число избыточных символов в переданной кодовой комбинации.
14. Особенности источников непрерывных сообщений.
Для непрерывных источников характерным является непрерывное изменение во времени или пространстве физического параметра, значение которого измеряется, обрабатывается (например, вычисляется плотность распределения вероятности) или передается на расстояние для получения информации (сведений) о том или ином явлении, факте, процессе и т.п.
При исследовании различных процессов или явлений производят измерение большого количества разнообразных физических величин: температуры, давления, освещенности, перемещений, скорости движения, механического напряжения, электрического напряжения, силы тока и т.п.
Обычно все разнородные физические величины в современных измерительных системах с помощью специальных первичных преобразователей (часто называемых датчиками) переводят из неэлектрической формы в стандартные электрические сигналы, например, в электрическое напряжение, изменяющееся в строго определенном диапазоне: от –1 В до +1 В, от –5 В до +5 В и др. В качестве примера датчика, преобразующего изменение температуры в технологическом процессе в электрическое напряжение, можно привести хорошо известную термопару. Структурная схема такого преобразования показана на рисунке.

Смысл этого
преобразования состоит в установке
некоторого соответствия между величинами
 и
и
 .
.
Подобно источникам дискретных сообщений, для источников непрерывных сообщений можно ввести количественные меры информации.
15. Полная и приведенная энтропия непрерывного источника информации.
Для того чтобы перейти от изучения источников дискретной информации к исследованию источников непрерывной информации, мы можем, как это обычно делается в математике, непрерывную величину, являющуюся переносчиком информации, приближенно представить как дискретную.
Почему это можно сделать. Значения параметров непрерывной величины получают в результате измерения. Все измерительные приборы имеют погрешность измерения и конечную разрешающую способность. Поэтому случайный непрерывный параметр Х может быть определен только с погрешностью ∆х. Вследствие этого можно перейти от непрерывного представления случайной величины к дискретному представлению.
Для этого диапазон
 изменения непрерывной случайной величины
делим на конечное число
изменения непрерывной случайной величины
делим на конечное число
 малых интервалов
малых интервалов
 и, перенумеровав их, можно совокупность
всех значений
и, перенумеровав их, можно совокупность
всех значений
 внутри
внутри
 -го
интервала представить одним средним
значением
-го
интервала представить одним средним
значением
 .
Априорная вероятность значения
.
Априорная вероятность значения
 выражается через функцию плотности
распределения вероятностей
выражается через функцию плотности
распределения вероятностей
 :
:
 .
.
Пример. Пусть
на выходе датчика (см. рисунок) формируется
напряжение в диапазоне от –5 В до +5 В ( = 10 В).
= 10 В).

Если это напряжение
измеряется стрелочным вольтметром с
ценой деления
 .=.0,1.В,
то в результате измерений мы, по сути,
заменяем непрерывную шкалу значений
выходного напряжения датчика дискретной
шкалой с числом интервалов измерений
.=.0,1.В,
то в результате измерений мы, по сути,
заменяем непрерывную шкалу значений
выходного напряжения датчика дискретной
шкалой с числом интервалов измерений
 .=.10.В./.0,1.В.=.100.
В результате одного
измерения (замера) мы получаем некоторое
количество информации, для оценки
которого мы можем воспользоваться
формулой энтропии дискретного источника
информации (1.6), которая в общем случае
с учетом выше изложенных обозначений
примет вид
.=.10.В./.0,1.В.=.100.
В результате одного
измерения (замера) мы получаем некоторое
количество информации, для оценки
которого мы можем воспользоваться
формулой энтропии дискретного источника
информации (1.6), которая в общем случае
с учетом выше изложенных обозначений
примет вид
 . (2.1)
. (2.1)
Устремляя
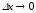 ,
проделаем широко используемое в
математике преобразование формулы
(2.1) к виду
,
проделаем широко используемое в
математике преобразование формулы
(2.1) к виду
 , (2.2)
, (2.2)
где
 будем называть полной энтропией источника
информации,
будем называть полной энтропией источника
информации,
 – плотностью распределения вероятностей
непрерывной случайной величины
– плотностью распределения вероятностей
непрерывной случайной величины
 или, для краткости, плотностью
распределения.
или, для краткости, плотностью
распределения.
В формуле (2.2) введен
дифференциал
 с учетом того, что
с учетом того, что
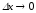 .
Однако в технике измерения и преобразования
непрерывных величин значение
.
Однако в технике измерения и преобразования
непрерывных величин значение
 (цена деления), каким бы малым ни было,
остается конечным, что учтено в (2.2), где
наряду с дифференциалом
(цена деления), каким бы малым ни было,
остается конечным, что учтено в (2.2), где
наряду с дифференциалом
 сохранено и обозначение
сохранено и обозначение
 .
.
Выражение (2.2) можно преобразовать следующим образом:

Учитывая, что
 [3], получим
[3], получим
 , (2.3)
, (2.3)
где первое слагаемое по структуре сходно с (1.6)
(1.6
начало) .
.
В данном случае
 является мерой количества информации,
приходящейся в среднем на одно достоверное
сообщение о событии
является мерой количества информации,
приходящейся в среднем на одно достоверное
сообщение о событии
 при передаче и преобразовании большого
числа
при передаче и преобразовании большого
числа
 таких сообщений.
таких сообщений.
Эту мера количества
информации предложил К. Шеннон. Она
более общая, чем мера Хартли, и получила
название энтропии конечного ансамбля
дискретных событий
 .(1.6
конец)
.(1.6
конец)
,
что позволило его назвать приведенной
энтропией источника непрерывной
информации
 :
:
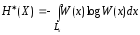 . (2.4)
. (2.4)
В технике измерений
и преобразований непрерывных величин
цена деления часто обозначается
 .
Поэтому в дальнейшем введем замену
.
Поэтому в дальнейшем введем замену
 и тогда формулу (2.3) представим как
и тогда формулу (2.3) представим как
 . (2.5)
. (2.5)
Примеры вычисления энтропии непрерывных источников информации:
2.3.1. Вычислить приведенную и полную энтропии источника с равномерным законом распределения непрерывной случайной величины.
Для такого источника
 (2.6)
(2.6)
Приведенную энтропию находим по формуле (2.4) с учетом (2.6):
 ,
,
откуда
 .
.
По формуле (2.5) находим полную энтропию
 . (2.7)
. (2.7)
Количественная
мера информации (2.7) согласуется с нашими
интуитивными представлениями. С
уменьшением
 ,
т.е. с повышением разрешающей способности
измерительных приборов, количество
получаемой в результате измерений
информации будет возрастать. При
,
т.е. с повышением разрешающей способности
измерительных приборов, количество
получаемой в результате измерений
информации будет возрастать. При
 ,
в при
,
в при
 ,
это соответствует случаю, когда измерения
не проводятся.
,
это соответствует случаю, когда измерения
не проводятся.
2.3.2. Вычислить приведенную и полную энтропии источника с нормальным законом распределения непрерывной случайной величины.
Для этого источника примем
 , (2.8)
, (2.8)
где
 – дисперсия источника, которая в данном
примере находится как
– дисперсия источника, которая в данном
примере находится как
 . (2.9)
. (2.9)
Приведенную энтропию для этого примера находим по формуле (2.4) как
 . (2.10)
. (2.10)
Вычисление этого интеграла дает
 . (2.11)
. (2.11)
Полную энтропию находим по формулам (2.5) и (2.11):
 .
.
В
приведенных примерах вычислялись
энтропии известных функций распределения.
Можно решать и задачи обратного характера,
например, найти функцию распределения
 ,
обеспечивающую максимальную энтропию
источника при некоторых заданных
ограничениях. Если таким ограничением
является диапазон изменения непрерывной
случайной величины источника, то
наибольшее значение энтропии дает
равномерное распределение. Если
ограниченной величиной является
дисперсия процесса при его неограниченном
диапазоне изменения, то наибольшее
значение энтропии достигается при
нормальном распределении.
,
обеспечивающую максимальную энтропию
источника при некоторых заданных
ограничениях. Если таким ограничением
является диапазон изменения непрерывной
случайной величины источника, то
наибольшее значение энтропии дает
равномерное распределение. Если
ограниченной величиной является
дисперсия процесса при его неограниченном
диапазоне изменения, то наибольшее
значение энтропии достигается при
нормальном распределении.
16. Энтропия источника с равномерным законом распределения.
Примеры вычисления энтропии непрерывных источников информации
Вычислить приведенную и полную энтропии источника с равномерным законом распределения непрерывной случайной величины.
Для такого источника
 (2.6)
(2.6)
Приведенную энтропию находим по формуле (2.4) с учетом (2.6):
 ,
,
откуда
 .
.
По формуле (2.5) находим полную энтропию
 . (2.7)
. (2.7)
Количественная
мера информации (2.7) согласуется с нашими
интуитивными представлениями. С
уменьшением
 ,
т.е. с повышением разрешающей способности
измерительных приборов, количество
получаемой в результате измерений
информации будет возрастать. При
,
т.е. с повышением разрешающей способности
измерительных приборов, количество
получаемой в результате измерений
информации будет возрастать. При
 ,
в при
,
в при
 ,
это соответствует случаю, когда измерения
не проводятся.
,
это соответствует случаю, когда измерения
не проводятся.
2.3.2. Вычислить приведенную и полную энтропии источника с нормальным законом распределения непрерывной случайной величины.
Для этого источника примем
 , (2.8)
, (2.8)
где
 – дисперсия источника, которая в данном
примере находится как
– дисперсия источника, которая в данном
примере находится как
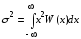 . (2.9)
. (2.9)
Приведенную энтропию для этого примера находим по формуле (2.4) как
 . (2.10)
. (2.10)
Вычисление этого интеграла дает
 . (2.11)
. (2.11)
Полную энтропию находим по формулам (2.5) и (2.11):
 .
.
В приведенных
примерах вычислялись энтропии известных
функций распределения. Можно решать и
задачи обратного характера, например,
найти функцию распределения
 ,
обеспечивающую максимальную энтропию
источника при некоторых заданных
ограничениях. Если таким ограничением
является диапазон изменения непрерывной
случайной величины источника, то
наибольшее значение энтропии дает
равномерное распределение. Если
ограниченной величиной является
дисперсия процесса при его неограниченном
диапазоне изменения, то наибольшее
значение энтропии достигается при
нормальном распределении.
,
обеспечивающую максимальную энтропию
источника при некоторых заданных
ограничениях. Если таким ограничением
является диапазон изменения непрерывной
случайной величины источника, то
наибольшее значение энтропии дает
равномерное распределение. Если
ограниченной величиной является
дисперсия процесса при его неограниченном
диапазоне изменения, то наибольшее
значение энтропии достигается при
нормальном распределении.
17. Энтропия источника с нормальным законом распределения.
Вычислить приведенную и полную энтропии источника с нормальным законом распределения непрерывной случайной величины.
Для этого источника примем
 , (2.8)
, (2.8)
где
 – дисперсия источника, которая в данном
примере находится как
– дисперсия источника, которая в данном
примере находится как
 . (2.9)
. (2.9)
Приведенную энтропию для этого примера находим по формуле (2.4) как
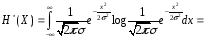 . (2.10)
. (2.10)
Вычисление этого интеграла дает
 . (2.11)
. (2.11)
Полную энтропию находим по формулам (2.5) и (2.11):
 .
.
В приведенных
примерах вычислялись энтропии известных
функций распределения. Можно решать и
задачи обратного характера, например,
найти функцию распределения
 ,
обеспечивающую максимальную энтропию
источника при некоторых заданных
ограничениях. Если таким ограничением
является диапазон изменения непрерывной
случайной величины источника, то
наибольшее значение энтропии дает
равномерное распределение. Если
ограниченной величиной является
дисперсия процесса при его неограниченном
диапазоне изменения, то наибольшее
значение энтропии достигается при
нормальном распределении.
,
обеспечивающую максимальную энтропию
источника при некоторых заданных
ограничениях. Если таким ограничением
является диапазон изменения непрерывной
случайной величины источника, то
наибольшее значение энтропии дает
равномерное распределение. Если
ограниченной величиной является
дисперсия процесса при его неограниченном
диапазоне изменения, то наибольшее
значение энтропии достигается при
нормальном распределении.
18. Количество информации в одном замере непрерывной случайной величины при неполной достоверности результатов измерения.
Количество информации, содержащееся в одном замере непрерывной случайной величины при неполной достоверности результатов измерения
Если бы измерение было абсолютно точным, т.е. не содержало погрешностей, то количество получаемой при этом информации, как уже отмечалось, должно было быть бесконечно большим.
В действительности,
однако, измерение любой величины может
быть выполнено лишь с некоторой степенью
точности. Наличие погрешностей приводит
к тому, что количество информации,
содержащееся в результате измерений
 ,
об измеряемой величине
,
об измеряемой величине
 становится конечным. Это позволяет
распространить соотношения, определяющие
становится конечным. Это позволяет
распространить соотношения, определяющие
 для дискретных источников информации,
на непрерывные источники.
для дискретных источников информации,
на непрерывные источники.
Для перехода от
дискретных источников к непрерывным,
как это уже делалось в разделе 2.2,
непрерывные величины
 и
и
 в первом приближении заменяем дискретными.
Тогда выражение (1.21) примет вид
в первом приближении заменяем дискретными.
Тогда выражение (1.21) примет вид
 . (2.12)
. (2.12)
В дроби, стоящей
под знаком логарифма, умножим числитель
и знаменатель на
 ,
тогда из (2.12) получим
,
тогда из (2.12) получим
 . (2.13)
. (2.13)
Переходя к пределу
 и
и
 ,
из (2.13) получаем
,
из (2.13) получаем
 . (2.14)
. (2.14)
Соотношение (2.14)
дает ответ на вопрос о количестве
информации, содержащейся в непрерывной
случайной величине
 ,
о непрерывной величине
,
о непрерывной величине
 .
.
Отметим некоторые свойства количественной меры информации (2.14).
2.4.1.
 .
Это следует из аналогии с дискретным
источником информации.
.
Это следует из аналогии с дискретным
источником информации.
2.4.2.
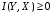 ,
причем
,
причем
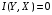 ,
если
,
если
 и
и
 – статистически независимые
случайные величины.
– статистически независимые
случайные величины.
2.4.3. Значение
 не зависит от способа отсчета величин
не зависит от способа отсчета величин
 и
и
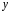 .
Если учесть, что
.
Если учесть, что
 ,
то выражение (2.14) может быть преобразовано
к виду
,
то выражение (2.14) может быть преобразовано
к виду
 , (2.15)
, (2.15)
где
 ,
,
 , (2.16)
, (2.16)
и может быть названо приведенной условной энтропией.
19.Приведите структурную схему цифрового канала.
Структурная схема цифрового информационного канала показана на рис.
На
вход такого канала обычно поступают
дискретные соотношения
 ,
например, в виде текста. Последние с
помощью кодирующего устройства
преобразуются в кодированные сигналы
,
например, в виде текста. Последние с
помощью кодирующего устройства
преобразуются в кодированные сигналы
 .
.

Рис. Структурная схема цифрового канала
Как
известно, для кодирования используется
некоторый алфавит элементарных сигналов
(символов) –
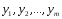 ,
а существо кодирования сводится к
представлению отдельных сообщений
,
а существо кодирования сводится к
представлению отдельных сообщений
 или последовательностей сообщений
некоторыми комбинациями символов
используемого алфавита. Декодирующее
устройство преобразует кодированные
сигналы
или последовательностей сообщений
некоторыми комбинациями символов
используемого алфавита. Декодирующее
устройство преобразует кодированные
сигналы
 в сообщения
в сообщения
 в форме, наиболее приемлемой для
получателя, которым может быть не только
человек, но и различные технические
устройства (принтер, монитор, ПЭВМ и
др.). В современных информационно-вычислительных
комплексах исходные сообщения
в форме, наиболее приемлемой для
получателя, которым может быть не только
человек, но и различные технические
устройства (принтер, монитор, ПЭВМ и
др.). В современных информационно-вычислительных
комплексах исходные сообщения
 могут быть и в непрерывной форме, но с
помощью кодирующих устройств последние
преобразуют в кодированные сигналы.
могут быть и в непрерывной форме, но с
помощью кодирующих устройств последние
преобразуют в кодированные сигналы.
20.Скорость передачи и пропускная способность цифровых каналов без помех.
На
вход такого канала обычно поступают
дискретные соотношения
 ,
например, в виде текста. Последние с
помощью кодирующего устройства
преобразуются в кодированные сигналы
,
например, в виде текста. Последние с
помощью кодирующего устройства
преобразуются в кодированные сигналы
 .
.

Рис. 3.1. Структурная схема цифрового канала
Как
известно, для кодирования используется
некоторый алфавит элементарных сигналов
(символов) –
 ,
а существо кодирования сводится к
представлению отдельных сообщений
,
а существо кодирования сводится к
представлению отдельных сообщений
 или последовательностей сообщений
некоторыми комбинациями символов
используемого алфавита. Декодирующее
устройство преобразует кодированные
сигналы
или последовательностей сообщений
некоторыми комбинациями символов
используемого алфавита. Декодирующее
устройство преобразует кодированные
сигналы
 в сообщения
в сообщения
 в форме, наиболее приемлемой для
получателя, которым может быть не только
человек, но и различные технические
устройства (принтер, монитор, ПЭВМ и
др.). В современных информационно-вычислительных
комплексах исходные сообщения
в форме, наиболее приемлемой для
получателя, которым может быть не только
человек, но и различные технические
устройства (принтер, монитор, ПЭВМ и
др.). В современных информационно-вычислительных
комплексах исходные сообщения
 могут быть и в непрерывной форме, но с
помощью кодирующих устройств последние
преобразуют в кодированные сигналы.
могут быть и в непрерывной форме, но с
помощью кодирующих устройств последние
преобразуют в кодированные сигналы.
3.1.1. Пропускная способность дискретных (цифровых) каналов
при отсутствии шумов
При
отсутствии шумов можно считать, что в
информационном канале
 ,
а
,
а
 ,
следовательно, для сообщений
,
следовательно, для сообщений
 ,
передаваемых за время
,
передаваемых за время
 ,
количество информации, поступающей к
получателю от источника, составит
,
количество информации, поступающей к
получателю от источника, составит
I(WT, XT) = I(XT, XT) = H(XT),
где Н(ХТ) – энтропия источника сообщений.
По аналогии для канала связи, представляющего часть информационного канала, будем иметь
I(ZT,YT) = I(YT, YT) = H(YT). (3.1)
Если последовательность хТ состоит из m сообщений и средняя длительность сигнала, обеспечивающего передачу одного сообщения, составляет с, то можно определить скорость передачи информации как
 , (3.2)
, (3.2)
где Н(X) – энтропия источника n сообщений:
 .
.
Очевидно,
что скорость передачи информации
 будет зависеть от статистических
характеристик источника сообщений,
метода кодирования сообщений и свойств
канала. Так, при одном и том же способе
кодирования длительность символов
передаваемых сигналов может быть
различной в зависимости от ширины полосы
частот пропускания канала. С изменением
длительности символов меняется и
скорость передачи информации.
будет зависеть от статистических
характеристик источника сообщений,
метода кодирования сообщений и свойств
канала. Так, при одном и том же способе
кодирования длительность символов
передаваемых сигналов может быть
различной в зависимости от ширины полосы
частот пропускания канала. С изменением
длительности символов меняется и
скорость передачи информации.
Пропускная способность информационного канала C определяется максимальным значением скорости передачи:

Аналогично находится пропускная способность канала связи Cс, являющегося частью информационного канала:
 (3.3)
(3.3)
Эффективное кодирование Обычно Cс C.
Реальная
скорость передачи информации может
быть максимальной и равной пропускной
способности канала, если статистические
характеристики источника сообщений
определенным образом согласованы со
свойствами информационного канала. Для
каждого источника это может быть
достигнуто специальным выбором способа
кодирования сообщений. Такое кодирование,
при котором достигается наиболее
эффективное использование пропускной
способности дискретного канала (т.е.
обеспечивается максимальная скорость
передачи информации
 ),
называется эффективным.
),
называется эффективным.
Дискретный
канал, в котором передаваемые сообщения
представлены двоичным кодом, называется
двоичным каналом. Если код имеет m
символов (разрядов), то очевидно, что
всего можно закодировать n
= 2m
сообщений, а
длительность одного сообщения составит
T
= m,
где

– длительность
символа кода с учетом того, что все
символы обычно имеют одинаковую
длительность. Двоичные коды, состоящие
из одинакового числа символов m,
называются равномерными. Пропускная
способность рассматриваемого канала
с учетом формул (3.1), (3.2) и (3.3) составит
– длительность
символа кода с учетом того, что все
символы обычно имеют одинаковую
длительность. Двоичные коды, состоящие
из одинакового числа символов m,
называются равномерными. Пропускная
способность рассматриваемого канала
с учетом формул (3.1), (3.2) и (3.3) составит
 . (3.4)
. (3.4)
Выражение (3.4) принимает максимальное значение, когда энтропия ансамбля событий (сообщений) H(YT) будет наибольшей. Из свойств энтропии следует, что H(YT) будет максимальна, если сообщения равновероятны, это максимальное значение может быть определено мерой Хартли и будет равно log n = log 2m = m.
Следует, однако, иметь в виду, что фактическая скорость передачи информации не всегда оказывается равной пропускной способности канала.
Рассмотрим два простых примера.
Пример 1. Пусть источник сообщений вырабатывает четыре сообщения х1, х2, х3, х4, (n = 4). Все сообщения имеют одинаковые вероятности: P(xi) = 1/n = 0,25. Для их кодирования используется двоичный равномерный код, число символов в котором достаточно выбрать m = 2. Исходные сообщения х1, х2, х3, х4 в этом примере будут представлены следующими кодами: 00, 01, 10, 11.
Скорость передачи информации будет определяться по формуле (3.2), в которой энтропия источника равновероятных сообщений будет максимальной:


а длительность каждого из четырех сообщений будет определяться длительностями соответствующих кодовых комбинаций и составит с=2. Для примера 1 по формуле (3.2) находим
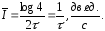
Таким образом, в
этом примере, как и следовало ожидать,
скорость передачи информации оказалась
равной пропускной способности канала:
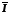 =Cc=1/.
=Cc=1/.
Пример 2. Источник сообщений и способ их кодирования такие же, как и в примере 1, но вероятности сообщения при этом не одинаковы:
Р(х1) = 0,5; Р(х2) = 0,25; Р(х3) = Р(х4) = 0,125.
Для определения скорости передачи информации вновь воспользуемся формулой (3.2), для которой необходимо вычислить соответствующее значение энтропии Н(х) для источника разновероятных сообщений х1, х2, х3, х4 (n = 4):

Длительности всех сообщений остаются такими же, как и в примере 1: с = 2. Скорость передачи информации составит

В этом примере скорость передачи информации оказалась меньше пропускной способности двоичного канала Cс (0,875/ 1/).
Таким образом, отход от оптимальных статистических характеристик сигналов приводит к тому, что фактическая скорость передачи информации становится меньше пропускной способности канала. Этот вывод естественным образом следует из самого понятия о пропускной способности канала.
Пример 1 показывает, что фактическая скорость передачи информации может быть максимальной и равной пропускной способности канала, если статистические характеристики источника сообщений определенным образом согласованы со свойствами информационного канала. Для каждого источника сообщений это согласование может быть достигнуто специальным выбором способа кодирования и декодирования сообщений. Такое кодирование, при котором достигается наилучшее использование пропускной способности канала, называется эффективным.
К эффективным относится, в частности, код Шеннона.-.Фано, пригодный для кодирования статистически независимых сообщений.
Рассмотрим построение кода Шеннона.-.Фано для источника сообщений х1, х2, х3, х4, приведенных в примере 2. Использование равномерного кода для этих сообщений, как отмечалось ранее, не позволяет обеспечить максимальную скорость передачи информации. Покажем, что с помощью кода Шеннона.-.Фано рассматриваемые сообщения можно передать с максимальной скоростью, равной пропускной способности двоичного канала. Кодирование сообщений в этом случае иллюстрируется табл. 3.1, которая составлена следующим образом.
Записывают сообщения в порядке убывания их вероятностей.
Таблица 3.1
|
Сообще-ние xi |
Вероят- ность р(хi) |
Номер деления на подгруппы |
Символ кода |
Длительность кодовой комбинации i |
||||||
|
Позиции |
||||||||||
|
1 |
2 |
3 |
1 |
2 |
3 |
|
||||
|
х1 |
0,5 |
|
|
|
0 |
|
|
1 |
||
|
х2 |
0,25 |
1 |
0 |
|
2 |
|||||
|
х3 |
0,125 |
1 |
1 |
0 |
3 |
|||||
|
х4 |
0,125 |
1 |
1 |
1 |
3 |
|||||
Проводят первое деление всех сообщений на две подгруппы I и II так, чтобы сумма вероятностей сообщений в подгруппах I и II была бы по возможности одинаковой. В данном случае это условие выполняется точно: при первом делении в подгруппу I входит сообщение х1, вероятность которого равна 0,5, а в подгруппу II входят сообщения х2, х3, х4, сумма вероятностей которых (0,25 + 0,125 + 0,125) будет тоже составлять 0,5.
Проводят второе аналогичное деление для каждой из полученных подгрупп сообщений. Процесс последовательных делений сообщений на подгруппы I и II прекращается в том случае, когда в подгруппе останется по одному сообщению.
Номер подгруппы, в которую попадает данное сообщение при каждом делении, определяет символ на соответствующей позиции кода этого сообщения. В рассматриваемой таблице принадлежность к подгруппе I обозначается символом 0, а к подгруппе II – символом 1. Так, в частности, первое деление дало на первой позиции кода для сообщения x1 символ 0, а для остальных сообщений – символ 1.
Как следует из табл. 3.1, полученный код является неравномерным, т.е. сигналы разных сообщений имеют различное число символов, следовательно, разную длительность.
Для наглядности в табл. 3.2 для сообщений х1, х2, х3, х4 приведены неравномерный код Шеннона - Фано и равномерный, используемый ранее в примерах 1 и 2. Анализируя неравномерный код Шеннона.-.Фано, можно убедиться в том, что наиболее вероятному сообщению соответствует самая короткая кодовая комбинация, наименее вероятному – длинная. Этим можно объяснить увеличение скорости передачи информации при использовании данного кода.
Таблица 3.2
|
Сообщение xi |
Код Шеннона - Фано |
Равномерный код |
|
x1 |
0 |
00 |
|
x2 |
10 |
01 |
|
x3 |
110 |
10 |
|
x4 |
111 |
11 |
Код Шеннона.-.Фано обладает еще одним существенным свойством: позволяет декодировать сообщения без введения дополнительных разделительных символов между кодовыми комбинациями, приводящих к снижению скорости передачи информации. Действительно, в рассмотренном примере короткие комбинации не совпадают с началом других, более длинных кодовых комбинаций. Поэтому возможно однозначное декодирование последовательности кодовых комбинаций, формируемых непрерывно без применения разделительных символов. Коды, удовлетворяющие рассмотренному условию, называются префиксными кодами.
Для
вычисления скорости передачи информации
при использовании кода Шеннона.-.Фано
воспользуемся формулой (3.2), применительно
к которой, как и в примере 2, Н(Х)
= 1,75,
 .
.
Как отмечалось ранее, код Шеннона.-.Фано является неравномерным. Поэтому целесообразно отыскать среднюю длительность сигнала с одного сообщения, определяемую по формуле математического ожидания длительности i сообщения xi [по аналогии с энтропией Н(Х)]:
 .
.
Для выбранного примера по табл. 3.1 (n = 4) находим с = 1,75, что позволяет считать кодовую комбинацию состоящей в среднем из m = 1,75 символа.
По формуле (3.2) для полученных значений Н(Х) и с находим скорость передачи:
 .
.
Таким
образом, в данном примере код Шеннона
- Фано позволил полностью согласовать
статистические характеристики источника
сообщений с каналом связи, поскольку
скорость передачи информации оказалась
равной пропускной способности канала:
 .
.
Равномерный код, как отмечалось в примере 2, не является эффективным. Это можно объяснить тем, что при использовании эффективного кода Шеннона.-.Фано сигнал каждого сообщения в среднем состоит из 1,75 символа, а при использовании равномерного кода – из 2-х (табл. 3.2), из чего следует, что в единицу времени сообщений, представленных кодом Шеннона.-.Фано, будет передано больше, чем при использовании равномерного кода.
Необходимо заметить и то, что, действуя по правилу построения кода Шеннона.-.Фано для четырех равновероятных сообщений, рассмотренных в примере 1, получаем приведенный в табл. 3.2 равномерный код, который в данном случае является эффективным.
Нарушение условия формирования кода Шеннона.-.Фано, заключающегося в том, что наиболее вероятному сообщению должна соответствовать наиболее короткая кодовая комбинация, неизбежно приведет к снижению скорости передачи информации.
Для
иллюстрации изложенного поменяем
местами кодовые комбинации для сообщений
х1
и х4
(см. табл. 3.1). Тогда по формуле математического
ожидания средняя длительность сообщения
увеличится и составит
 ,
а скорость передачи информации
,
а скорость передачи информации

Проследим еще, что дают различные способы кодирования на примере 3.
Пример 3. Источник сообщений описывается как
 .
.
Коррелятивные
связи между сообщениями отсутствуют.
Передача информации производится по
двоичному каналу. Длительность символов
кодированного сигнала равна
 .
Определим скорость передачи информации
при использовании равномерного кода и
кода Шеннона - Фано.
.
Определим скорость передачи информации
при использовании равномерного кода и
кода Шеннона - Фано.
Используя (1.6), находим

или
 .
.
Согласно (3.2) скорость передачи информации равна
 .
.
При равномерном коде для передачи каждого сообщения придется израсходовать два символа (табл. 3.3).
Таблица 3.3
|
Сообщение |
Код |
|
x1 |
00 |
|
x2 |
01 |
|
x3 |
10 |
Очевидно,
что в этом случае
 и, следовательно,
и, следовательно,
 ,
,
где
 – пропускная
способность данного канала.
– пропускная
способность данного канала.
Для построения кода Шеннона - Фано составлена табл. 3.4.
Таблица 3.4
|
Сообще-ние
|
Вероят- ность
|
Номер деления на подгруппы |
Символ кода |
Длительность сигнала |
|||||
|
1 |
2 |
|
1 |
2 |
3 |
||||
|
х1 |
0,7 |
|
|
|
0 |
|
|
1 |
|
|
х2 |
0,2 |
1 |
0 |
2 |
|||||
|
х3 |
0,1 |
1 |
1 |
2 |
|||||
Средняя длительность сигнала при этом будет
 .
.
Скорость передачи информации в этом случае равна
 .
.
Как
видим, переход к более эффективному
коду позволяет увеличить
скорость передачи информации в
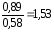 раза.
раза.
Эффективность кодирования может быть еще увеличена, если от кодирования одиночных сообщений перейти к кодированию последовательностей (групп) сообщений (табл. 3.5).
Таблица 3.5
|
Сооб-щение |
Вероят- ность |
Деление на подгруппы |
Код |
Длитель- ность сигнала |
|||||||
|
х2х2 х1х2 х2х1 х2х3 х3х2 х1х1 х1х3 х3х1 х3х3 |
0,49 0,14 0,14 0,07 0,07 0,04 0,02 0,02 0,01 |
|
|
|
|
|
|
0 1 0 0 1 0 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 1 |
3 3 4 4 4 5 6 6 |
||
В табл. 3.5 дано построение кода Шеннона.-.Фано для случая передачи всех возможных пар сообщений.
Средняя длительность сигнала, обеспечивающего передачу одного сообщения, в этом случае будет
 .
.
Соответствующая скорость передачи сообщений равна
 .
.
Если кодировать последовательности по три и более сообщений, то скорость передачи информации может еще больше приблизиться к пропускной способности.
Кодирование последовательностей сообщений особенно эффективно при наличии коррелятивных связей между ними. Легко видеть, что кодирование отдельных сообщений кодом Шеннона.-.Фано коррелятивных связей не учитывает. При кодировании же последовательностей сообщений вероятности этих последовательностей будут вычисляться с учетом коррелятивных связей. Кроме того, с удлинением кодируемых сообщений коррелятивные связи между ними ослабевают.
Заметим еще, что описанный метод построения эффективного кода Шеннона.-.Фано может быть распространен и на коды с основанием больше двух.
Рассмотренные
примеры построения эффективных кодов
согласуются с основной
теоремой Шеннона для дискретного канала
без помех.
Теорема формулируется следующим образом:
если поток информации
 ,
вырабатываемой источником, равен Н(Х)
= Сс
– ,
где
– сколь угодно малая величина, то всегда
можно найти такой способ кодирования,
который обеспечивает передачу всех
сообщений, вырабатываемых источником,
причем скорость передачи
,
вырабатываемой источником, равен Н(Х)
= Сс
– ,
где
– сколь угодно малая величина, то всегда
можно найти такой способ кодирования,
который обеспечивает передачу всех
сообщений, вырабатываемых источником,
причем скорость передачи
 =
Сс
–
.
=
Сс
–
.
Обратное
утверждение состоит в том, что невозможно
обеспечить передачу всех сообщений
источника, у которого
 .
.
21. Какое кодирование называется эффективным?
Фактическая скорость передачи информации может быть максимальной и равной пропускной способности канала, если статистические характеристики источника сообщений определенным образом согласованы со свойствами информационного канала. Для каждого источника сообщений это согласование может быть достигнуто специальным выбором способа кодирования и декодирования сообщений. Такое кодирование, при котором достигается наилучшее использование пропускной способности канала, называется эффективным.
Дискретный
канал, в котором передаваемые сообщения
представлены двоичным кодом, называется
двоичным каналом. Если код имеет m
символов (разрядов), то очевидно, что
всего можно закодировать n
= 2m
сообщений, а длительность одного
сообщения составит T
= m,
где

– длительность
символа кода с учетом того, что все
символы обычно имеют одинаковую
длительность. Двоичные коды, состоящие
из одинакового числа символов m,
называются равномерными. Пропускная
способность рассматриваемого канала
с учетом формул (3.1), (3.2) и (3.3) составит
– длительность
символа кода с учетом того, что все
символы обычно имеют одинаковую
длительность. Двоичные коды, состоящие
из одинакового числа символов m,
называются равномерными. Пропускная
способность рассматриваемого канала
с учетом формул (3.1), (3.2) и (3.3) составит
 . (3.4)
. (3.4)
Выражение (3.4) принимает максимальное значение, когда энтропия ансамбля событий (сообщений) H(YT) будет наибольшей. Из свойств энтропии следует, что H(YT) будет максимальна, если сообщения равновероятны, это максимальное значение может быть определено мерой Хартли и будет равно log n = log 2m = m.
Следует, однако, иметь в виду, что фактическая скорость передачи информации не всегда оказывается равной пропускной способности канала. смотри выше, там есть еще пример
Возможность построения эффективных кодов согласуется с основной теоремой Шеннона для дискретного канала без помех.
Теорема
формулируется следующим образом: если
поток информации![]() ,
вырабатываемой источником сообщений,
равен
,
вырабатываемой источником сообщений,
равен
![]() – сколь угодно малая величина, то всегда
можно найти такой способ кодирования,
который обеспечивает передачу всех
сообщений, вырабатываемых источником,
причем скорость передачи информации
будет сколь угодно близка к пропускной
способности канала:
– сколь угодно малая величина, то всегда
можно найти такой способ кодирования,
который обеспечивает передачу всех
сообщений, вырабатываемых источником,
причем скорость передачи информации
будет сколь угодно близка к пропускной
способности канала:![]() .
.
Обратное
утверждение состоит в том, что невозможно
обеспечить передачу всех сообщений
источника, у которого![]() .
.
К эффективным относится, в частности, код Шеннона.-.Фано, пригодный для кодирования статистически независимых сообщений.
22. Построение кода Шеннона-Фано
Рассмотрим построение кода Шеннона.-.Фано для источника сообщений х1, х2, х3, х4, приведенных в примере 2. Использование равномерного кода для этих сообщений, как отмечалось ранее, не позволяет обеспечить максимальную скорость передачи информации. Покажем, что с помощью кода Шеннона.-.Фано рассматриваемые сообщения можно передать с максимальной скоростью, равной пропускной способности двоичного канала. Кодирование сообщений в этом случае иллюстрируется табл. 3.1, которая составлена следующим образом.
Записывают сообщения в порядке убывания их вероятностей.
Таблица 3.1
|
Сообще-ние xi |
Вероят- ность р(хi) |
Номер деления на подгруппы |
Символ кода |
Длительность кодовой комбинации i |
||||||
|
Позиции |
||||||||||
|
1 |
2 |
3 |
1 |
2 |
3 |
|
||||
|
х1 |
0,5 |
|
|
|
0 |
|
|
1 |
||
|
х2 |
0,25 |
1 |
0 |
|
2 |
|||||
|
х3 |
0,125 |
1 |
1 |
0 |
3 |
|||||
|
х4 |
0,125 |
1 |
1 |
1 |
3 |
|||||
Проводят первое деление всех сообщений на две подгруппы I и II так, чтобы сумма вероятностей сообщений в подгруппах I и II была бы по возможности одинаковой. В данном случае это условие выполняется точно: при первом делении в подгруппу I входит сообщение х1, вероятность которого равна 0,5, а в подгруппу II входят сообщения х2, х3, х4, сумма вероятностей которых (0,25 + 0,125 + 0,125) будет тоже составлять 0,5.
Проводят второе аналогичное деление для каждой из полученных подгрупп сообщений. Процесс последовательных делений сообщений на подгруппы I и II прекращается в том случае, когда в подгруппе останется по одному сообщению.
Номер подгруппы, в которую попадает данное сообщение при каждом делении, определяет символ на соответствующей позиции кода этого сообщения. В рассматриваемой таблице принадлежность к подгруппе I обозначается символом 0, а к подгруппе II – символом 1. Так, в частности, первое деление дало на первой позиции кода для сообщения x1 символ 0, а для остальных сообщений – символ 1.
Как следует из табл. 3.1, полученный код является неравномерным, т.е. сигналы разных сообщений имеют различное число символов, следовательно, разную длительность.
Для наглядности в табл. 3.2 для сообщений х1, х2, х3, х4 приведены неравномерный код Шеннона - Фано и равномерный, используемый ранее в примерах 1 и 2. Анализируя неравномерный код Шеннона.-.Фано, можно убедиться в том, что наиболее вероятному сообщению соответствует самая короткая кодовая комбинация, наименее вероятному – длинная. Этим можно объяснить увеличение скорости передачи информации при использовании данного кода.
Таблица 3.2
|
Сообщение xi |
Код Шеннона - Фано |
Равномерный код |
|
x1 |
0 |
00 |
|
x2 |
10 |
01 |
|
x3 |
110 |
10 |
|
x4 |
111 |
11 |
Код Шеннона.-.Фано обладает еще одним существенным свойством: позволяет декодировать сообщения без введения дополнительных разделительных символов между кодовыми комбинациями, приводящих к снижению скорости передачи информации. Действительно, в рассмотренном примере короткие комбинации не совпадают с началом других, более длинных кодовых комбинаций. Поэтому возможно однозначное декодирование последовательности кодовых комбинаций, формируемых непрерывно без применения разделительных символов. Коды, удовлетворяющие рассмотренному условию, называются префиксными кодами.
Для
вычисления скорости передачи информации
при использовании кода Шеннона.-.Фано
воспользуемся формулой (3.2), применительно
к которой, как и в примере 2, Н(Х)
= 1,75,
 .
.
Как отмечалось ранее, код Шеннона.-.Фано является неравномерным. Поэтому целесообразно отыскать среднюю длительность сигнала с одного сообщения, определяемую по формуле математического ожидания длительности i сообщения xi [по аналогии с энтропией Н(Х)]:
 .
.
Для выбранного примера по табл. 3.1 (n = 4) находим с = 1,75, что позволяет считать кодовую комбинацию состоящей в среднем из m = 1,75 символа.
По формуле (3.2) для полученных значений Н(Х) и с находим скорость передачи:
 .
.
Таким
образом, в данном примере код Шеннона
- Фано позволил полностью согласовать
статистические характеристики источника
сообщений с каналом связи, поскольку
скорость передачи информации оказалась
равной пропускной способности канала:
 .
.
Равномерный код, как отмечалось в примере 2, не является эффективным. Это можно объяснить тем, что при использовании эффективного кода Шеннона.-.Фано сигнал каждого сообщения в среднем состоит из 1,75 символа, а при использовании равномерного кода – из 2-х (табл. 3.2), из чего следует, что в единицу времени сообщений, представленных кодом Шеннона.-.Фано, будет передано больше, чем при использовании равномерного кода.
Необходимо заметить и то, что, действуя по правилу построения кода Шеннона.-.Фано для четырех равновероятных сообщений, рассмотренных в примере 1, получаем приведенный в табл. 3.2 равномерный код, который в данном случае является эффективным.
Нарушение условия формирования кода Шеннона.-.Фано, заключающегося в том, что наиболее вероятному сообщению должна соответствовать наиболее короткая кодовая комбинация, неизбежно приведет к снижению скорости передачи информации.
Для
иллюстрации изложенного поменяем
местами кодовые комбинации для сообщений
х1 и х4 (см. табл. 3.1).
Тогда по формуле математического
ожидания средняя длительность сообщения
увеличится и составит
 ,
а скорость передачи информации
,
а скорость передачи информации

Проследим еще, что дают различные способы кодирования на примере 3.
Пример 3. Источник сообщений описывается как
 .
.
Коррелятивные
связи между сообщениями отсутствуют.
Передача информации производится по
двоичному каналу. Длительность символов
кодированного сигнала равна
 .
Определим скорость передачи информации
при использовании равномерного кода и
кода Шеннона - Фано.
.
Определим скорость передачи информации
при использовании равномерного кода и
кода Шеннона - Фано.
Используя (1.6), находим

или
 .
.
Согласно (3.2) скорость передачи информации равна
 .
.
При равномерном коде для передачи каждого сообщения придется израсходовать два символа (табл. 3.3).
Таблица 3.3
|
Сообщение |
Код |
|
x1 |
00 |
|
x2 |
01 |
|
x3 |
10 |
Очевидно,
что в этом случае
 и, следовательно,
и, следовательно,
 ,
,
где
 – пропускная способность данного
канала.
– пропускная способность данного
канала.
Для построения кода Шеннона - Фано составлена табл. 3.4.
Таблица 3.4
|
Сообще-ние
|
Вероят- ность
|
Номер деления на подгруппы |
Символ кода |
Длительность сигнала |
|||||
|
1 |
2 |
|
1 |
2 |
3 |
||||
|
х1 |
0,7 |
|
|
|
0 |
|
|
1 |
|
|
х2 |
0,2 |
1 |
0 |
2 |
|||||
|
х3 |
0,1 |
1 |
1 |
2 |
|||||
Средняя длительность сигнала при этом будет
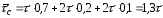 .
.
Скорость передачи информации в этом случае равна
 .
.
Как
видим, переход к более эффективному
коду позволяет увеличить скорость
передачи информации в
 раза.
раза.
Эффективность кодирования может быть еще увеличена, если от кодирования одиночных сообщений перейти к кодированию последовательностей (групп) сообщений (табл. 3.5).
Таблица 3.5
|
Сооб-щение |
Вероят- ность |
Деление на подгруппы |
Код |
Длитель- ность сигнала |
|||||||
|
х2х2 х1х2 х2х1 х2х3 х3х2 х1х1 х1х3 х3х1 х3х3 |
0,49 0,14 0,14 0,07 0,07 0,04 0,02 0,02 0,01 |
|
|
|
|
|
|
0 1 0 0 1 0 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 1 |
3 3 4 4 4 5 6 6 |
||
В табл. 3.5 дано построение кода Шеннона.-.Фано для случая передачи всех возможных пар сообщений.
Средняя длительность сигнала, обеспечивающего передачу одного сообщения, в этом случае будет
 .
.
Соответствующая скорость передачи сообщений равна
 .
.
Если кодировать последовательности по три и более сообщений, то скорость передачи информации может еще больше приблизиться к пропускной способности.
Кодирование последовательностей сообщений особенно эффективно при наличии коррелятивных связей между ними. Легко видеть, что кодирование отдельных сообщений кодом Шеннона.-.Фано коррелятивных связей не учитывает. При кодировании же последовательностей сообщений вероятности этих последовательностей будут вычисляться с учетом коррелятивных связей. Кроме того, с удлинением кодируемых сообщений коррелятивные связи между ними ослабевают.
Заметим еще, что описанный метод построения эффективного кода Шеннона.-.Фано может быть распространен и на коды с основанием больше двух.
Рассмотренные
примеры построения эффективных кодов
согласуются с основной теоремой
Шеннона для дискретного канала без
помех. Теорема формулируется следующим
образом: если поток информации
 ,
вырабатываемой источником, равен Н(Х)
= Сс
– ,
где – сколь
угодно малая величина, то всегда можно
найти такой способ кодирования, который
обеспечивает передачу всех сообщений,
вырабатываемых источником, причем
скорость передачи
,
вырабатываемой источником, равен Н(Х)
= Сс
– ,
где – сколь
угодно малая величина, то всегда можно
найти такой способ кодирования, который
обеспечивает передачу всех сообщений,
вырабатываемых источником, причем
скорость передачи
 =
Сс
–
.
=
Сс
–
.
Обратное
утверждение состоит в том, что невозможно
обеспечить передачу всех сообщений
источника, у которого
 .
.