
- •Вопрос 2.
- •Часть 1.Количественная мера информации для равновозможных событий
- •Часть 2. Мера р. Хартли
- •Вопрос 3.
- •Вопрос 4.
- •Вопрос 5.
- •Вопрос 6. Свойства энтропии источника дискретных сообщений
- •Вопрос 7. Энтропия источника совместных сообщений
- •Вопрос 8. Что такое условная энтропия?
- •Вопрос 9.
- •Вопрос 10. Свойства количественной меры информации при неполной достоверности результатов опыта.
- •Вопрос 11. Вычисление количественной меры информации для двоичного канала с помехами.
- •Вопрос 12. Как оценивается избыточность источника сообщений?
- •Вопрос 13.
- •Вопрос 23.
- •Вопрос 24. Приведите модель двоичного канала с шумами
- •Вопрос 25.
- •Вопрос26. Формула Шеннона для аналогового канала с шумами.
- •Вопрос 27. Энтропия источника при наличии коррелятивных связей между двумя соседними символами
- •Вопрос 28. Принципы помехоустойчивого кодирования. Кодовое расстояние.
- •Вопрос 29. Вероятность ошибочного приема кодовой информации для простого двоичного кода и для кода с исправлением ошибок кратности t.
- •Вопрос 30. Простейшие избыточные коды.
- •Вопрос 31. Групповой код Хемминга. Принципы построения. Синдром ошибки. Коды с обнаружением и исправлением ошибок. Код хемминга
- •Вопрос 32. Определение числа проверочных элементов.
- •Вопрос 33. Определение проверочных элементов, входящих в каждую группу. Исправляющая способность кода хемминга
Вопрос 5.
Пример
вычисления
 .
Вычислим энтропию двоичного канала как
источника информации. В таком канале
передаются два символа «0» и «1», т.е.
ансамбль событий можно представить как
.
Вычислим энтропию двоичного канала как
источника информации. В таком канале
передаются два символа «0» и «1», т.е.
ансамбль событий можно представить как
 ,
,
где
событие
 соответствует символу «0», а событие
соответствует символу «0», а событие
 – символу «1».
– символу «1».
Обозначим
для простоты записи
 ,
а
,
а
 [не забываем, что
[не забываем, что
 ],
по формуле (1.6) находим
],
по формуле (1.6) находим
 (1.7)
(1.7)
Для
построения графика зависимости
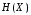 от
от
 определим
определим
 для трех значений
для трех значений
 :
:

Здесь имеется два вида неопределенности: в первом слагаемом при р=0, а во втором – при р=1 получаем log(0), который, как известно, не существует
Для
раскрытия неопределенности для первого
слагаемого выражения (1.7) при малых
значениях
 рассмотрим предел, к которому стремится
это слагаемое:
рассмотрим предел, к которому стремится
это слагаемое:
 .
Здесь – log
p
представлен как log 1 – log p.
.
Здесь – log
p
представлен как log 1 – log p.
Обозначив
 и воспользовавшись правилом Лопиталя,
т.е. взяв производные по α от числителя
и знаменателя, получим
и воспользовавшись правилом Лопиталя,
т.е. взяв производные по α от числителя
и знаменателя, получим
 .
.
Таким
образом, при значении

 .
.
Нетрудно
убедиться, что при

 ,
а при
,
а при

 .
.
На
рис. 1.1 приведен график зависимости
 от
от
 ,
полученный по формуле (1.7).
,
полученный по формуле (1.7).
Из
этого графика видно, что энтропия
 при
при
 и
и
 ,
,
 имеет максимальное значение
имеет максимальное значение
 при
при
 .
Эти результаты нетрудно объяснить:
действительно, при
.
Эти результаты нетрудно объяснить:
действительно, при
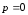 априорно известно, что в канале передаются
только символы «1», и сообщение об этом,
т.е. их прием на выходе канала, не несет
информации.
априорно известно, что в канале передаются
только символы «1», и сообщение об этом,
т.е. их прием на выходе канала, не несет
информации.
Аналогично
при
 ,
когда в канале передаются только символы
«0», сообщение не несет информации.
,
когда в канале передаются только символы
«0», сообщение не несет информации.

При
 символы «0» и «1» будут иметь одинаковую
вероятность и наличие каждого из этих
символов будет иметь наибольшую
неопределенность. Поэтому достоверный
прием на выходе канала конкретного
символа будет полностью устранять эту
неопределенность, и это сообщение,
получаемое в результате приема, будет
обеспечивать получение максимального
количества информации:
символы «0» и «1» будут иметь одинаковую
вероятность и наличие каждого из этих
символов будет иметь наибольшую
неопределенность. Поэтому достоверный
прием на выходе канала конкретного
символа будет полностью устранять эту
неопределенность, и это сообщение,
получаемое в результате приема, будет
обеспечивать получение максимального
количества информации:
 ,
т.е. в двоичном канале, когда вероятности
обоих символов одинаковы, достоверный
прием любого из них несет 1 дв.
ед. информации.
,
т.е. в двоичном канале, когда вероятности
обоих символов одинаковы, достоверный
прием любого из них несет 1 дв.
ед. информации.
В данном случае имеем равновероятные события, для которых справедлива мера Хартли: I=log22=1 дв.ед.
Вопрос 6. Свойства энтропии источника дискретных сообщений
В
соответствии с (1.6) энтропия
 источника дискретных сообщений
источника дискретных сообщений
 .
.
-
Энтропия есть величина вещественная, неотрицательная и ограниченная.
Выделим
из формулы для энтропии (1.6) одно слагаемое
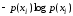 и докажем, что это слагаемое является
величиной вещественной, неотрицательной
и ограниченной. Заметим, что для крайних
значений
и докажем, что это слагаемое является
величиной вещественной, неотрицательной
и ограниченной. Заметим, что для крайних
значений
 и
и
 рассматриваемое
слагаемое обращается в нуль. При этом
для значения
рассматриваемое
слагаемое обращается в нуль. При этом
для значения
 необходимо
рассмотреть предел, который использован
в примере для двоичного канала.
необходимо
рассмотреть предел, который использован
в примере для двоичного канала.
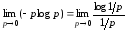 .
.
Здесь р перевели в знаменатель в виде дроби 1/р. В числителе остается –logp, который представлен как log1/p=log1– logp = –logp, т.к. log1=0.
Обозначив
 и воспользовавшись правилом Лопиталя,
получим
и воспользовавшись правилом Лопиталя,
получим
 .
.
Для
значений
 интересующее нас слагаемое будет
вещественным и неотрицательным. Для
доказательства ограниченности величины
интересующее нас слагаемое будет
вещественным и неотрицательным. Для
доказательства ограниченности величины
 найдем
найдем
 ,
при котором исследуемая величина примет
максимальное значение. Для этого, как
известно, надо отыскать производную и
приравнять ее нулю:
,
при котором исследуемая величина примет
максимальное значение. Для этого, как
известно, надо отыскать производную и
приравнять ее нулю:
 ,
,
Решая
приведенное выше уравнение, получаем .
.
Этому
значению
будет соответствовать максимальное
значение слагаемого –p(xi)log(p(xi)),
равное 0,531. Таким образом, интересующее
нас слагаемое
 является вещественным, неотрицательным
и ограниченным. График зависимости
величины этого слагаемого от
является вещественным, неотрицательным
и ограниченным. График зависимости
величины этого слагаемого от
 приведен на рис..1.2.
Поскольку энтропия представляет собой
ограниченную сумму слагаемых, то
свойства для одного слагаемого в данном
случае можно перенести на всю сумму.
приведен на рис..1.2.
Поскольку энтропия представляет собой
ограниченную сумму слагаемых, то
свойства для одного слагаемого в данном
случае можно перенести на всю сумму.

-
Энтропия
 лишь
в том случае, когда все вероятности
лишь
в том случае, когда все вероятности
 ,
кроме одной, равны нулю, а эта единственная
вероятность равна единице.
Следовательно,
,
кроме одной, равны нулю, а эта единственная
вероятность равна единице.
Следовательно,
 только в
случае полной определенности исхода
опыта, а в остальных случаях
только в
случае полной определенности исхода
опыта, а в остальных случаях
 .
Последнее
вытекает из того, что
.
Последнее
вытекает из того, что
 и, как было
доказано в п.1.4.1,
и, как было
доказано в п.1.4.1,
 .
. -
При заданном
 энтропия максимальна и равна
энтропия максимальна и равна
 лишь тогда, когда все события
равновероятны,
т.е.
лишь тогда, когда все события
равновероятны,
т.е.
 .
.
Это
свойство можно доказать следующим
образом. Для краткости записи обозначим
 и
представим (1.6) в виде
и
представим (1.6) в виде
 . (1.8)
. (1.8)
Поскольку все события xi независимы и несовместны, то сумма их вероятностей равна 1. Тогда применительно к (1.8) должно выполняться условие
 . (1.9)
. (1.9)
Найдем
значения
 ,
при которых энтропия
,
при которых энтропия
 имеет максимальное значение.
имеет максимальное значение.
Согласно правилу отыскания относительного максимума функции нескольких переменных с учетом (1.8) и (1.9) имеем
 ,
,
где
 – множитель Лагранжа.
– множитель Лагранжа.
Подставляем
в последнее равенство значения
 из
(1.8)
и, выполнив дифференцирование, получаем
из
(1.8)
и, выполнив дифференцирование, получаем
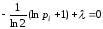 ,
,
откуда
 ,
(1.10)
,
(1.10)
где
 .
.
Заметим,
что с учетом (1.10)
 ,
откуда
следует
,
откуда
следует ,
что соответствует равной вероятности
событий. Найденное экстремальное
значение
,
что соответствует равной вероятности
событий. Найденное экстремальное
значение
 соответствует максимуму энтропии.
Изложенное свойство энтропии 1.4.3
полностью согласуется с графиком
зависимости
соответствует максимуму энтропии.
Изложенное свойство энтропии 1.4.3
полностью согласуется с графиком
зависимости
 от
от
 на рис. 1.1 для двоичного канала как
источника информации.
на рис. 1.1 для двоичного канала как
источника информации.
