1rabinovich_s_g_pogreshnosti_izmereniy

При прямых измерениях с точным оцениванием погрешностей всегда можно различать средства измерений, показания которых дают оценку измеряемой величины (назовем их условно основными), и средства измерений влияющих величин. Обычно индивидуально устанавливают свойства только основных средств измерений, для остальных ограничиваются данными нормативных документов.

Для основных средств измерений при этом находят оценки их систематических погрешностей. Случайные погрешности можно вообще не оценивать, так как при статистических измерениях они войдут в результаты наблюдений и будут учтены при обработке последних. Далее находят функции влияния тех влияющих величин, которые при измерении могут оказаться за пределами области их нормальных значений. Если таких величин несколько, то нужно выяснить, нет ли среди их функций влияния такой, которая существенно зависит от другой влияющей величины. Если есть такая, то целесообразно ее находить примерно при, том значении другой влияющей величины, какое она будет иметь при измерении.

Установив таким образом индивидуальные свойства основных средств измерений, при эксперименте затем измеряют все влияющие величины.

	Если, например,	для влияющей	величины			E j , получена	оценка	~
								E j , а
	коэффициент ее	~	оценка систематической				погрешности,
		влияния Wj , то
				~	~ ~
	обусловленной этой величиной, будет ϑi = Wj Ej .
	Алгебраическая сумма всех найденных оценок элементарных
	систематических погрешностей дает поправку
			æ	k ~	l	~ ö
		C = -çç		åϑ0i + åϑj ÷÷ ,
	~		è i=1		j=1	ø
		систематической		погрешности i-го основного средства
	где ϑ0i — оценка

измерений в нормальных условиях (i = 1,...,k ).

Суммированием по i предусматривается, что при прямом измерении в число основных может входить несколько средств измерений. Например,

при измерении напряжения с помощью потенциометра к основным средствам измерений относятся потенциометр, нормальный элемент и делитель напряжения.

Как известно, поправками погрешности устраняются неполностью, остаются неисключенные остатки систематических погрешностей. Каждая

из них дает одну из элементарных систематических погрешностей результата. Используя обозначения, принятые нами для систематических погрешностей, элементарные систематические погрешности будем обозначать символом ϑj (j = 1,...,m,m = k + l).

Систематическая составляющая основной погрешности 1-го средства измерений оценивается с погрешностью, определяемой погрешностью образцовых средств измерений.

Неисключенный остаток погрешности, вызванной j-й влияющей, величиной, определяется неточностью измерения этой величины и неточностью определения ее коэффициента влияния. Заметим, что оценивается эта погрешность методами, которые относятся к задачам, косвенных измерений и рассматриваются в гл. 6.

Как одну из элементарных погрешностей нужно рассматривать и возможную динамическую погрешность. Соображения о путях оценивания этой погрешности приведены в § 5-3.

Кроме того, иногда неполностью устраняются методические погрешности, могут иметь место систематические погрешности, обусловленные индивидуальными свойствами, экспериментатора. Эти составляющие также следует оценить, считая их элементарными погрешностями.

Как отмечалось в гл. 4, по мыслимому множеству измерений одной и той же величины, выполняемых одним и тем же методом, но с помощью других средств измерений (естественно, обеспечивающих предусмотренную методом измерения точность), эти систематические погрешности можно рассматривать как случайные величины и на этой основе их суммировать.

Если бы реализация каждой элементарной систематической погрешности ϑj была известна, то их сумма дала бы общую систематическую

погрешность результата, которую можно было бы устранить введением поправки. Но реализации элементарных погрешностей остаются неизвестными, для каждой из них обычно находят только оценку ее границ θ j :

−θ j ≤ ϑj ≤ +θ j .

В этих условиях, как было отмечено, в § 4-3, распределение

элементарных систематических погрешностей целесообразно считать равномерным.

Если принять, что все элементарные погрешности имеют равномерное распределение, то по формуле (4-3) можно найти доверительные границы систематической погрешности результата измерения:

m
θ = k åθ j2	,	(5-4)
j =1

где т — число элементарных систематических погрешностей.

Как отмечалось в § 4-4, при т < 4 целесообразно проверить, соблюдается

	m
ли условие	θ ≤ åθ j	. Если это неравенство не выполняется, то в качестве
	j =1

оценки границ неисключенной погрешности результата измерения нужно взять

m

θ = åθ j

j =1

Если границы некоторых элементарных погрешностей не равны по модулю, т. е, они не симметричны относительно нулевого значения, то вычисления выполняются несколько иначе.

Пусть, например, границы погрешности ϑr равны θrн и θrв , причем θrн ¹ θrв . Тогда, найдя среднее значение

ϑ = θrв +θrн ,

r 2

можно перейти к симметричным относительно среднего границам θr .

θr =

θrв −θrн

=θrв -ϑr =ϑr -ϑrв .

2

Обычно погрешность ϑr

можно устранить, введя поправку Cr = -ϑr .

Тогда все дальнейшие расчеты выполняются по приведенной выше схеме, причем для погрешности ϑr в расчет вводят уже только ее границы θr .

Однако иногда из осторожности поправки на средние значения элементарных погрешностей (или части их) не вводятся. Тогда границы

систематической погрешности результата измерения находят следующим образом. Сначала, алгебраически сложив найденные средние элементарные погрешности, вычисляют среднюю погрешность результата измерения

s

ϑ = åϑr .

r =1

Далее вычисляют сумму симметричных погрешностей

s

θc = k åθr2 .

r=1

Оцениваемые границы систематической погрешности результата измерения будут

θн =ϑ -θс и θв =ϑ +θс .

Среднее квадратичеекое отклонение для ϑ можно вычислить по формуле

	m	(ϑi	) =	1	m
	Sϑ = åS2				åθ j2 .	(5-5)
	j =1			3 j =1

Рассмотренным выше методом суммировались условно постоянные систематические погрешности. Для безусловно постоянных составляющих не представляется возможным обосновать статистическую модель. С одной стороны, потому, что измерение конкретной величины в заданной точностью в принципе возможно очень ограниченным числом методов. С другой стороны,

эти погрешности

часто связаны с определением истинного значения конкретной измеряемой величины, т. е. с пороговым несоответствием модели объекту. При измерениях и

истинное значение измеряемой величины и изучаемое свойство объекта исследования всегда рассматриваются в детерминистском плане.

По приведенной причине безусловно постоянные систематические составляющие приходится суммировать алгебраически. Если θб.н р и θб.в р —

нижняя и верхняя границы р-й элементарной безусловно постоянной систематической погрешности, то границы их суммы будут

	r									r
θ	б.н = åθб.н р			и θ			б.в = åθб.в р .
	p=1									p=1
Обычно, как отмечалось, r < 3 и			θб.н р			,		θб.в р		невелики.

Границы условно постоянных и безусловно постоянных систематических погрешностей приходится складывать тоже алгебраически. Таким образом,

верхнюю и нижнюю границы систематической погрешности результата измерения можно найти по формулам:

θв =θб.в +θ и θн =θб.н −θ .

Итак, мы имеем результат измерения и оценки параметров его случайной и систематической погрешности. Нужно отметить, что поскольку за результат измерения принимаем среднее арифметическое результатов наблюдений, то оценка случайной погрешности характеризует возможное, хотя и не наблюдавшееся, рассеивание средних арифметических; Оценки границ

систематической погрешности характеризуют точно так же возможную смещенность среднего арифметического.

В ряде случаев раздельная оценка систематической и случайной погрешности результата исчерпывает задачу оценивания погрешности результата измерений.

Однако часто необходимо найти общую погрешность измерения, включающую в себя и случайную и систематическую составляющие.

Постановка данной задачи вызывала и вызывает много дискуссий. В статье [65] отмечается, что хотя с принципиальных позиций систематические и случайные погрешности складывать нельзя, но опыт и интуиция показывают возможность сложения этих погрешностей. Какие же принципиальные позиции имеются в виду? Только то, что систематические и случайные погрешности имеют разную природу. Но и те и другие выражаются в одних единицах и, что действительно является принципиальным, при законченном измерении физически неразделимы, т. е. они физически

складываются: измеряя А, получим А. Разность ~ − содержит и систематическую и случайную

A A

составляющую. При анализе погрешности, теоретическим или экспериментальном, мы раскладываем эту погрешность на составляющие: систематическую и случайную. Естественно, что правомерна и обратная задача — задача сложения составляющих.

Из приведенных выше соображений следует, что при решении рассматриваемой задачи и условно постоянные систематические,

и случайные погрешности можно рассматривать как случайные величины.

Объединение двух случайных величин связано с построением композиции их распределений. Однако построение композиций распределений слишком сложно для практики. Поэтому в работах [23, 41] построены вспомогательные графики, дающие приближенное решение задачи. Но графики все же недостаточно удобны, и во всяком случае предпочтительно иметь аналитическое решение.

На практике часто границу общей погрешности вычисляют по формуле

D =θ + tq Sx .

Эта формула достаточно проста, но ясно, что дает заведомо преувеличенную оценку. Более правдоподобную оценку для можно найти следующий путем [31, 43].

Среднее квадратическое отклонение общей погрешности результата

Så = Sx2 + Sϑ2 .			(5-6)
Оценки для Sx и Sϑ находим по формулам (5-2) и (5-5). Имея			Så ,

границу погрешности результата можно было бы вычислить по формуле

D = tå Så ,	(5-7)
если был бы известен коэффициент tå ; к сожалению,	этот коэффициент

неизвестен.

Поскольку исходные данные, т. е. данные о составляющих общей погрешности, известны неточно, то можно удовлетвориться и приближенной оценкой коэффициента tå . Для такой приближенной

оценки предложена формула [43]:

	tå	=	ψ x	+θ	.	(5-8)
			Sx	+ Sϑ

Эта формула была подобрана ца основе следующих соображений. Коэффициент tq , определяющий соотношение между доверительной границей

и средним квадратическим отклонением случайной погрешности, определяется распределением Стьюдента и известен. Имея оценки для θ и Sϑ , можно считать, что известен аналогичный коэффициент для

систематической погрешности

tϑ =θSϑ

Искомой коэффициент tå естественно считать какой-то функцией tq и tϑ , отвечающих одной и той же вероятности. В качестве такой функции

взято среднее взвешенное из tq

и tϑ с весами

Sϑ

и

Sx

соответственно,

что приводит к формуле

Sx

+ Sϑ

Sx + Sϑ

tqSx

+ t

S

ψ

+θ

t

å

=

ϑ

ϑ

=

x

.

(5-9)

Sx

+ Sϑ

Sx

+ Sϑ

z1−r

Для того чтобы можно было пользоваться этой формулой, необходимо оценить ее точность. Крайними являются случаи, когда систематическая погрешность имеет нормальное или равномерное распределение.

Распределение случайной погрешности среднего арифметического можно считать асимптотически нормальным.

Если оба слагаемых имеют нормальное распределение, то tq = tϑ и, как следует из формулы (5-9), tå = tq . Поскольку композиция нормальных распределений дает нормальное распределение, то полученное значение tå

является точным.

Для второго случая нужно сопоставить результаты вычислений по приближенной формуле (5-8) с полученными по точно построенной композиции нормального и равномерного распределений.

Из теории вероятностей известно выражение для плотности распределения суммы двух независимых централизованных случайных величин, одна из которых имеет нормальное, а вторая — равномерное распределение:

f (z)=	1	h		1			e−	(z− y )2
		ò						2σ 2	dy ,
	2h	−hσ			2π

где h — половина интервала, на котором равномерно распределена случайная величина Y. Положив σ =1 и перейдя к интегральной функции распределения, находим

		1		z h	(z − y )2
	F (z)= 0,5 +			ò òe−	2 dydz .	(5-10)
	z >0	2h 2π		0 −h

Исходные распределения симметричны относительно нуля. Поэтому плотность результирующего распределения также обладает этим свойством. Нам нужно найти границы доверительного интервала, отвечающего вероятности α . Для этого достаточно найти либо квантиль

zr уровня r , либо квантиль уровня 1− r , так как zr = z1−r . Поскольку α =1− 2r , то r = 1-2α . Очевидно, что r < 0,5 и zr < 0 .

Втабл. 5-1 приведены значения z1−r , найденные с использованием формулы.(5-10) для

α= 0,90;0,95 и 0,99 .

Относительная погрешность, вызванная применением приближенной формулы (5-8), будет

δ = D - z1−z .

Сравнение следует проводить при Så

= σå , имея в виду, что Sx = σ =1. При этом

æ h ö2

2

h2

1

σ

å

= σ

+

=σ 1+

ç

÷ .

3

3

è σ ø

Поэтому, введя коэффициент t

=

z1−r

, с учетом (5-7) получим

r

σå

δ =

tå - tr

.

(5-11)

tr

Таблица 5-1

Характерные квантили композиции центрированных нормального (σ = 1) и равномерного ( h = var ) распределений

h	0,50	1,0	2,0	3,0	4,0	5,0	6,0	8,0	10
z0,95 (α = 0,90)	1,71	1,90	2,49	3,22	4,00	4,81	5,65	7,34	9,10
z0,95 (α = 0,95)	2,04	2,25	2,90	3,67	4,49	5,34	6,22	8,00	9,81
z0,95 (α = 0,99)	2,68	2,94	3,66	4,49	5,36	6,26	7,17	9,02	10,9

Коэффициент tr зависит только от конфигурации результирующего распределения, т. е. от

соотношения между	h и σ ,		а не от их абсолютных значений.					Поэтому ряд значений этого
коэффициента можно вычислить по данным табл. 5-1, Эти значения приведены в табл. 5-2.
Значения коэффициента tr										Таблица 5-2
					в зависимости от параметров
	нормального и равномерного распределений
h σ	0,5		1	2	3	4		5	6	8	10
σå (σ =1)	1,04		1,15	1,53	2,00	2,52		3,06	3,51	4,72	5,85
t0,95 (α = 0,90)	1,65		1,64	1,63	1,61	1,59		1,58	1,57	1,56	1,55
t0,975 (α = 0,95)	1,96		1,95	1,90	1,84	1,78		1,75	1,72	1,69	1,67
t0,995 (α = 0,99)	2,57		2,54	2,40	2,24	2,13		2,05	1,99	1,91	1,86

Теперь снова обратимся к приближенной формуле (5-8). Границы доверительного интервала,

определяемые по равномерному распределению, дают θ .
Поскольку r =	h -θ	и r =	1-α	,
			2
	2h
				θ = (1- 2r)h = αh .			(5-12)
Граница доверительвого интервала для нормального распределения при той же
доверительной вероятности будет
				Dx = z1+α σ ,			(5-13)
					2

где z1+α — квантиль нормированного нормального распределения.

2

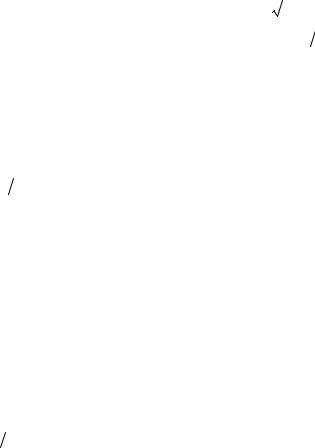
Формула (5-8) с учетом (5-12) и (5-13) принимает вид

										z1+α +α						h
								tå =								σ				.
										2
												1
										1+					×	h
										3						σ
Значения tå ,	вычисленные для тех же отношений h σ и доверительных вероятностей, что
были взяты при вычислении tr					приведены в табл. 5-3. В табл. 5-4 сведены вычисленные на основе
данных табл. 5-2 и 5-3 и формулы (5-11) погрешности δ .																										Таблица 5-3
Значение коэффициента tå в зависимости от параметров
			нормального и равномерного распределений
h σ			0,50			1,0		2,0		3,0										4,0		5,0		6,0	8,0		10
t1å (α = 0,90)			1,63			1,61		1,60		1,59										1,58		1,58		1,58	1,57		1,57
t2å (α = 0,95)			1,89			1,84		1,79		1,76										1,74		1,73		1,72	1,70		1,69
t3å (α = 0,99)			2,38			2,26		2,11		2,03										1,97		1,94		1,91	1,87		1,84
											tå															Таблица 5-4
															от		t			r (в процентах)
	Отклонения коэффициента
h σ		0,50			1,0			2,0		3,0							4,0					5,0		6,0		8,0	10
δ1(α = 0,90)		1,2			1,9			1,8		1,1							0,6					0		0,8		0,6	1,2
δ2 (α = 0,95)		3,6			5,5			5,7		4,1							2,2					1,3		0		0,5	1,0
δ3(α = 0,99)		7,4			11			12		9,4							7,3					5,5		4,0		2,2	1,1

Таким образом, сопоставление результатов точных расчетов и результатов расчетов с использованием приближенной формулы (5-8) показывает,

что погрешности от применения приближенной формулы во всех случаях отрицательны и по модулю не превышают 12% (при α = 0,99). Это свидетельствует о возможности пользоваться формулой (5-8).

Следует, к тому же, заметить, что рассматриваемая погрешность снижается по мере того, как распределение систематических погрешностей приближается к нормальному.

z1−r (h),

Приведенную схему оценивания погрешности результата измерения, содержащего и случайную и систематическую составляющие, надо рассматривать как общую. В различных конкретных задачах она может соответственно трансформироваться. Так, А. И. Механников в статье [38] рассматривает случай радиотехнических измерений, когда в

погрешность результата входят так называемые погрешности рассогласования. При равномерном распределении фазы, что принимается априори, погрешности рассогласования имеют арккосинусное распределение. Для суммирования погрешностей с таким распределением в статье приведены полезные графики и формулы.

Остановимся еще на вопросе о том, когда можно пренебречь систематической или случайной составляющей погрешности.

На рис. 5-1 на основе данных табл. 5-1 построены графики

соответствующие композиции нормального и равномерного распределений и равномерным распределениям. Сравнивая кривые 1 со значениями z1−r нормального распределения (точки

при h=0), можно найти погрешность от пренебрежения систематической составляющей погрешности результата измерения. Если принять, что эта погрешность не должна превышать 15%, то получим предельные отношения hσ . В зависимости от доверительной вероятности эти отношения равны:

α	…	0,90	0,95	0,99
h σ	…	1,2	1,1	1,1

Если пренебрегать случайной составляющей, то возникающая погрешность определяется разностью ординат точной кривой 1 и прямой 2 при данном h (линии 1,2 на рис. 5-1). Ориентируясь на ту же погрешность 15%, получим условие возможности пренебречь нормально распределенной составляющей:

α	…	0,90	0,95	0,99
h σ	…	3	4	7

Естественно, что пренебрежение любой из составляющих сопровождается уменьшением общей погрешности.

Таким образом, если hσ <1, то с достаточной уверенностью можно пренебрегать систематической, а если h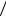σ > 7 — случайной составляющей

погрешности результата измерения.

Правда, мы имеем вместо точных значений параметров h и σ их оценки θ и S. Поэтому, чтобы быть строгими, вместо σ следует брать верхнюю границу

доверительного интервала при решении вопроса о возможности пренебрежения случайной составляющей погрешности и нижнюю границу — при выяснении возможности пренебрежения систематической составляющей.

В рассмотренной схеме суммирования случайных и систематических погрешностей не учитывалась безусловно постоянная систематическая составляющая погрешности. Если эта погрешность имеет место, то ее следует присоединить к полученной оценке путем алгебраического суммирования.

Нужно заметить, что при измерении со значительной случайной погрешностью обычно стремятся сделать такое число наблюдений, чтобы

случайная погрешность среднего арифметического стала пренебрежимо малой по сравнению с систематической погрешностью среднего арифметического.

Приведенная методика позволяет оценивать погрешности статистических измерений, при которых многократные наблюдения выполняют с, целью уменьшения случайных погрешностей результата. При измерениях средних величин и в других ситуаццях, когда имеют место квазислучайные погрешности, методика оценивания погрешностей в принципе остается той же, что приведена выше. Однако квазислучайные погрешности априори нельзя считать имеющими нормальное распределение.

Рассмотренная выше методика ориентирована на статистические измерения с точным оцениванием погрешностей. При статистических

измерениях с приближенным оцениванием погрешностей свойства используемых средств измерений учитывают на