1rabinovich_s_g_pogreshnosti_izmereniy

данном случае вообще возможно только тогда, когда рассеивание результатов наблюдений обнаруживает определенные закономерности; при хаотическом

разбросе результатов наблюдений совместно обработать их и получить результат измерения невозможно. Поэтому на первом этапе постановки измерения необходимо убедиться в том, что отмеченная выше закономерность имеет место. В этом случае говорят, что распределение наблюдений обладает статистической устойчивостью, или подконтрольностью.

На важность проверки статистической устойчивости наблюдений обращают внимание и математики [52, 53] и метрологи [64]. На практике при

изучении нового метода измерения или нового по существу средства измерений выполняется столько наблюдений (и в таких условиях), сколько необходимо для того, чтобы у экспериментатора появилась уверенность в устойчивости получаемых результатов. Без этой устойчивости даже большому числу

наблюдений нельзя поставить в соответствие вероятностную модель и дать на ней определение истинного значения измеряемой величины, т.е. нельзя осуществить измерение с заданной точностью.

Погрешности несколько иной природы, называемые обычно тоже случайными, возникают при измерениях средних величин. Например, измеряется средний диаметр цилиндра. Если фиксировать координаты каждого измеренного диаметра, то каждый результат будет неслучайным. Поэтому по самой сути явления наблюдаемые отклонения от среднего будут неслучайными. Однако в

некоторых случаях в соответствии с целью измерения их можно рассматривать как случайные.

Погрешности измерений средних величин, обусловленные неслучайными различиями усредняемых величин при подходе к ним как к случайным, следует отличать от погрешностей, случайных по сути своей. Для этого их целесообразно называть, например, квазислучайными погрешностями.

В данной главе приводятся основные математические методы, необходимые

для обработки результатов наблюдений при измерениях со значительными случайными погрешностями. Рассматривается ситуация, непосредственно соответствующая прямым измерениям, свободным от систематических погрешностей.

3-2. Способы описания случайных погрешностей

Случайные погрешности проявляются в том, что повторные измерения одной и той же величины, казалось бы, в одних и тех же условиях приводят к результатам, отличающимся один от другого.

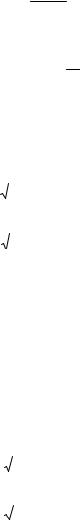
Как мы отмечали в гл. 1, отдельный результат, т. е. отдельное значение случайной погрешности, предсказать невозможно. Но большая совокупность случайных погрешностей какого-то измерения подчиняется определенным закономерностям. Эти закономерности — статистические, вероятностные. Они устанавливаются и используются в метрологии на основе методов математической статистики и теории вероятностей.

Полностью свойства случайной величины описываются функцией распределения F(х), которая определяет вероятность того, что случайная величина X будет меньше х:

F(x)= P(X < x).

Функция распределения — неубывающая функция, определенная так, что F(- ¥)= 0 , а

F(+ ¥)=1.

Наряду с функцией распределения F(х), называемой кумулятивной или интегральной, широко применяется дифференциальная, обычно называемая плотностью распределения f(х):

f (x)= dFdx(x).

Обратим внимание на то, что плотность распределения — функция размерная: dim f (x)= dim X1 .

В практике точных измерений чаще всего имеют дело с нормальным и равномерным распределениями. На рис. 3-1, а приведены кумулятивные функции этих распределений, а на рис. 3-1, б — функции плотности этих же распределений. Для нормального распределения имеем:

f (x)=		1			−	(x− A)2			ü
					e 2σ 2 ,				ï
	σ		2π						ï	(3-1)
					x		(x− A)2		ý
F(x)=		1				−			ï
						e 2σ 2			dx.ï
	σ		2π	ò					ï
					−∞				þ

Параметр σ 2 — дисперсия, А — математическое ожидание случайной величины (истинное значение

измеряемой величины при отсутствии систематических погрешностей).

P{X < xф}= Pф . При

Вычисление F(х) при некотором фиксированном хф

дает

вероятность

использовании графика f (x)

для вычисления этой вероятности

нужно найти

площадь под кривой,

расположенную левее точки х

на рис. 3-1, б.

При расчетах широко применяется нормированное нормальное распределение, которое получается при

переходе к случайной величине z =

X - A

:

σ

1

−

z 2

ü

2

ï

f (z)=

2π e

,

ï

(3-2)

1

z

y2

ý

F(z)=

e−

dy.ï

2

2π

ò

ï

−∞

þ

Часто приводят таблицы значений функции Ф(z), определяемой выражением
Ф(z)=		1
			z	−	y2			(3-3)
		2π òe			2 dy

0

и называемой нормированной функцией Лапласа. Очевидно, что для Z ³ 0

F(z)=0,5+Ф(z).

Рис. 3-1. Интегральные (а) и дифференциальные (б) функции нормального (слева) и равномерного (справа) распределений непрерывных случайных величин

Ветвь для Z<0 находится на основе соображений симметрии

F{z)=0,5-Ф(z).

Таблицы для функций f (z) и Ф(z) приведены в приложении (табл. П-1 и П-2).

Нормальное распределение замечательно тем, что согласно центральной предельной теореме это

распределение имеет сумма бесконечно большого числа бесконечно малых случайных величин с любым распределением. На практике сумма сравнительно небольшого числа погрешностей уже оказывается близкой к нормальному распределению.

Равномерное распределение:

ì					x < d	ü
ï		0				ï
ï						ï
f (x)= í		1	,		d £ x £ bý
ïb - d						ï	(3-4)
ï		0,			x > b	ï
î						þ
ì x - d						ü
ï						ï
			,
F(x)= í					d £ x £ b,ý
ïb - d					x > b.	ï
î		1,				þ

Равномерное распределение мы также будем часто использовать.

Кроме непрерывных случайных величин, в метрологии встречаются и дискретные случайные величины. Пример интегральной функции распределения и распределения вероятностей дискретной случайной величины приведен на рис. 3-2.

Функции распределений являются полными характеристиками случайных величин, но они не всегда удобны для практики. Поэтому для описания случайных величин применяют и их числовые характеристики. С этой целью используют моменты случайных величин: начальные и центральные.

Начальный mk и центральный μk моменты k-гопорядка определяютсяформулами:

∞	ü
mk = M [X k ]= òxk f (x),ï
−∞	ï	(3-5)
	ý
n	ï
mk = M [X k ]= åxik pi .
	ï
i =1	þ

Здесь и в соотношениях (3-6) — (3-8) первая формула относится к непрерывным, а вторая — к дискретным случайным величинам;

	∞			ü
μk = M [X - M [x]]k = ò(x - M [X ])k f (x)dx,ï
	−∞			ï	(3-6)
				ý
k	n	k		ï
μk = M [X - M [x]] =	å(x - M [X ])		pi .	ï
	i=1			þ
Из начальных моментов чаще всего используется первый момент (k					=1) — математическое
ожидание случайной величины
m1 = M [X ]	∞	ü
	= òxf (x)dx,ï
	−∞	ï			(3-7)
		ý
	n	ï
m1 = M [X ]= åxi pi .
		ï
	i =1	þ

n
Предполагается, что å pi =1, т. е. что рассматривается полная группа событий.
i=1
Из центральных моментов особенно важную роль играет второй момент (k=2) — дисперсия
случайной величины
μ2 = D[X ]= M [(X - m1 )2 ]= ò∞ (x - m1 )2 f (x)dx,
−∞	(3-8)
μ2 = D[X ]= M [(X - m1 )2 ]= ån	(xi - mi )2 pi .

i=1

Положительный корень квадратный из дисперсии носит название среднего квадратического отклонения случайной величины

σ = +		(3-9)
	D[X ]

Соответственно D[x]= σ 2 .

Находят еще применение третий и четвертый центральные моменты, с помощью которых можно охарактеризовать симметричность и островершинность распределений. Первое качество

характеризуют асимметрией a = μ3 , второе — эксцессом σ 3

e =	μ4	.
	σ 4
	Нормальное		распределение	полностью

характеризуется двумя параметрами: m1 = A и σ . Для

него характерно, что а=0, е= 3.

Равномерное распределение тоже определяется двумя параметрами: т1=А и l = d − b . Известно, что

m =

d + b

,

ü

ï

1

2

ï

(3-10)

D[X ]=

(d -b)2

l2

ý

=

ï

12

ï

12þ

Часто вместо l применяют h = l

2 .Тогда

D[X ]=

h2

и σ (X )=

h

.

3

3

Рис. 3-2. Интегральная функция рас- пределения (а) и распределение веро- ятностей (б) дискретной случайной

величины

Как было обосновано в гл.1, измеряемой величиной, несмотря на наличие случайных погрешностей, может быть только величина, определенная на модели как неслучайная и постоянная. Задача состоит в том, чтобы по полученным экспериментально данным найти наилучшую оценку истинного значения измеряемой величины.

К оценкам, получаемым по статистическим данным, предъявляются требования состоятельности, несмещенности и эффективности.

~

Оценка A называется состоятельной, если при увеличении числа

наблюдений она стремится к истинному значению оцениваемой величины А (по вероятности сходится к А):

~æ		ö	® A .
Aç x1	,..., xn ÷
è	n→∞	ø

Оценка А называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемой величины:

[~]=

M A A .

В том случае, когда можно найти несколько несмещенных оценок, лучшей из них, естественно, считается та, которая имеет меньшую дисперсию. Чем меньше дисперсия оценки, тем более эффективной называют эту оценку.

Способы нахождения оценок измеряемой величины и показателей их качества зависят от вида функции распределения наблюдений.

При нормальном распределении наблюдений в качестве оценки истинного значения измеряемой величины можно принять среднее арифметическое результатов наблюдений, а можно и их медиану. Отношение дисперсий этих оценок, которые приведены, например, в книге [29, стр. 404], равно

σ2 =

x0,6

σm2

(σ x2 — дисперсия среднего арифметического, σm2 — дисперсия медианы).

Следовательно, среднее арифметическое является более эффективной оценкой А, чем медиана.

При равномерном распределении в качестве оценки А можно взять среднее арифметическое результатов наблюдений или полусумму размаха:

	~		1	n	~		xmin + xmax
	A1	=	n	åxi	или A	=		,
							2
				i=1

Отношение дисперсий этих оценок известно [29, стр. 407]:

D				~		=		(n +1)(n + 2) .
				~
				A1
D		A2						6n

При п = 2 отношение дисперсий равно единице, а затем растет. Так, при n = 10 это отношение уже равно 2,2. Следовательно, полусумма размаха в данном случае — более эффективная оценка, чем среднее арифметическое.

Если иметь функцию распределения наблюдений, то можно наилучшим образом решать многие задачи метрологии. Однако дли практики функции распределения, как правило, недоступны.

Если случайный характер результатов наблюдений обусловлен погрешностями измерений, обычно принимают, что наблюдения имеют нормальное распределение. Результаты вычислений, основанные на этом допущения, как правило, не приводят к противоречиям. Вероятно, это обусловлено двумя причинами. Во-первых, погрешности измерений складываются из многих составляющих. Согласно центральной предельной теореме это ведет в пределе к нормальному распределению. Кроме того, измерения, для которых существенна оценка точности, выполняются в контролируемых условиях, в результате чего распределения их погрешностей оказываются ограниченными. Поэтому их аппроксимация нормальным распределением, допускающим любые значения случайной величины, приводит к некоторым запасам,

например к более широким доверительным интервалам, чем те, которые можно было бы получить, зная истинное распределение. На данное обстоятельство указывает, например, Е. Ф. Долинский [20].

Однако известны примеры, когда результаты наблюдений при измерениях не соответствуют нормальному распределению [24, 66]. Кроме того, когда измеряемой величиной является среднее значение, то распределение наблюдений может иметь любой вид. Поэтому гипотеза о нормальности распределения наблюдений должна проверяться.

Методы статистических расчетов для наблюдений, подчиняющихся

нормальному распределению хорошо разработаны и обеспечены необходимыми таблицами. Если же гипотезу о нормальности распределения приходится отвергнуть, то статистическая обработка наблюдений существенно усложняется. Математики работают над тем, чтобы найти если и не лучшие, то все же удовлетворительные оценки для параметров распределения, неточно установленных по форме.

Случайные и квазислучайные погрешности статистических измерений всегда оценивают по полученным в ходе измерения экспериментальным данным. Оценка случайной погрешности обыкновенных измерений, если она представляет интерес, находится расчетным путем. При этом общая случайная погрешность измерения часто находится на основе суммирования составляющих. Однако

суммирование погрешностей является типичной задачей оценивания систематических погрешностей, и поэтому методы решения этой задачи приведены не в этой, а в следующей главе.

Составляющие погрешности измерения, которые применительно к целям данного измерения не требуется подвергать дальнейшему расчленению, будем называть элементарными погрешностями измерения.

Обычно элементарные погрешности измерения можно оценить, опираясь на опыт и интуицию: При этом предпочтение отдается простейшему, чаще всего равномерному распределению, для которого сравнительно легко оценить границы.

Например, погрешность измерения иногда определяется погрешностью от трения в опорах подвижной части измерительного прибора. Распределение наблюдений в этом случае обычно считают равномерным, хотя в

действительности оно может быть и более близким к усеченному нормальному распределению.

При радиотехнических измерениях часто приходится учитывать погрешность от рассогласования участков линий. Эта погрешность выражается с помощью тригонометрических функций. За элементарную погрешность при этом принимают погрешность определения фазы процесса и считают, что она имеет равномерное распределение. Обусловленная ею погрешность

рассогласования при этом приобретает так называемое арккосинусное распределение [41, 38].

Можно отметить, что в качестве моделей распределений элементарных случайных погрешностей всегда принимают центрированные распределения, и чаще всего — симметричные относительно нулевого значения.

3-3. Оценивание параметров нормального распределения

Если имеющиеся данные не противоречат гипотезе о нормальном распределении наблюдений, то для полной характеристики распределения нужно найти оценки для М[X]=А и σ .

Когда известна функция плотности вероятностей случайной величины, то

оценивание ее параметров можно осуществить методом наибольшего правдоподобия [49, 56]. Воспользуемся этим методом для решения нашей задачи.

Элементарная вероятность получить некоторый результат наблюдения xt

в интервале	xi ±	Dxi	равна fi (xi , A,σ )Dxi . Все результаты наблюдений
	2

независимы. Поэтому вероятность встретить все экспериментально полученные наблюдения при Dxi = ... = Dxn равна

n

Pl = ∏ fi (xi , A,σ )Dx1...Dxn .

i=1

Идея метода состоит в том, что за оценки параметров распределения (в нашем случае это параметры А и σ ) берут такие значения, которые дают

максимум вероятности Pl . Задача решается, как обычно, путем приравнивания нулю частных производных Pl по оцениваемым параметрам. Постоянные сомножители не влияют на решение, и поэтому рассматривают только произведение функций fi , которое называется функцией правдоподобия

n

L(x1,..., xn ; A,σ )= ∏ fi (x1,..., xn ; A,σ ).

i=1

Вернемся к нашей задаче. Для имеющейся группы наблюдений x1,..., xn

значения функции плотности вероятностей будут

	(x , A,σ )=		1			e−	(xi − A)2
f							2σ 2	.
i	i	σ		2π

Следовательно,

1

n

æ

1 ö

n

−

å(xi − A)2

2

e

2σ

i 1

.

L = ç

÷

=

è

σ

2π

ø

Для нахождения максимума L удобно исследовать ln L :

n

n

2

1

n

2

ln L = −

2 ln 2π − 2 lnσ

−

å(xi − A) .

2σ

2

i=1

Максимум L будет при

∂L

= 0 и

∂L

= 0 :

∂A

2

∂σ

∂L

1

n

(xi − A)= 0,

=

å

L∂A

2

∂L

σ

i=1

n

1

n

= −

+

å(xi − A)2 = 0.

2

)

2

2σ

4

L∂(σ

2σ

i=1

Из первого уравнения находим оценку для А;

~

1

n

A = n

åxi .

(3-11)

i=1

2

1

n

2

Второе уравнение даст оценку σ*

= n

å(xi − A) . Но А неизвестно; взяв

вместо А его оценку x получим

i=1

~2

1

n

2

σ

*

= n

å(xi

− x)

.

(3-12)

i=1

Проверим, являются ли полученные оценки состоятельными и

несмещенными. Математическое

ожидание

M (xi )= A ,

так

как все

xi

относятся к одному и тому же распределению. Поэтому

~

1

n

M [A]= n åM (xi )= A .

i=1

~

несмещенной

оценкой

A .Она

является

и

Следовательно, A является

~

состоятельной оценкой, так как при n → ∞ A → A по закону больших чисел.

Перейдем к исследованию σ*2 . В формуле (3-12) случайными являются и xi

и x . Поэтому перепишем ее следующим образом:

2

1

n

2

σ* =

n

å(xi − A + A − x) =

i=1

=1 å[(xi - A)2 - 2(xi - A)(x - A)+ (x - A)2 ]=

n i=1

		1 n	2		2		n
=		å(xi - A)		-		å(xi - A)(x - A)+
		n i=1			n i=1
+	1	n	2	1	n		2	2
		å(x - A) =			å(xi - A)			-(x - A)	,
	n i=1			n i=1

так как

1 ån (xi - A)2 = (x - A)2

n i=1

и

2 ån (xi - A)(x - A) =

n i=1

=2 (x - A)ån (xi - A) = 2(x - A)2.

n i=1

~2
Найдем M [σ* ]. Для этого надо учесть следующие соотношения. По
определению, согласно (3-8) и (3-9) имеем M (xi - A)2						= σ 2 . Следовательно,
é1	n	2	ù	1	é n	2	= σ	2	ù
M ê	å(xi -	A)	ú =	n	M êå(xi - A)				ú.
ën i=1			û		ë i=1				û
Для случайной	величины			x	аналогично		можно написать

M (x - A)2 = D[x]. Выразим D[х] через σ 2 = D[X ]:

é1

n

ù

1

n

1

σ 2

D[x]= Dê

åxi ú =

åD(xi ) =

D[X ]=

.

n

2

n

n

ën i=1

û

i=1

Таким образом,

~2

2

σ 2

n -1

2

M [σ*

]= σ

-

=

σ

n

n

.

~2

является смещенной. Но при

Следовательно, полученная по (3-12) оценка σ*

n → ∞ M [σ*2 ]® σ 2 , следовательно, эта оценка состоятельная.