т. Однофазные электрические цепи переменного тока. 8

Лекция №5 Частотные свойства электрических цепей.

Частотные свойства электрических цепей

1. Задачи исследования электрических цепей

2. Дифференциальные уравнения цепи.

3. Преобразования Фурье и Лапласа.

4. Передаточные функции.

5. Частотные функции и характеристики.

6. Входные и передаточные функции цепей синусоидального тока.

7. Логарифмические частотные характеристики (самостоятельно).

Задачи исследования электрических цепей

Сформулированные уравнения являются исходными при определении токов и напряжений цепи с заданными структурой и параметрами, находящейся под действием внешних источников.

При анализе цепи иногда требуется произвести полный расчет — определить все токи и напряжения на всех ее элементах. В большинстве случаев необходимо оп­ределить лишь часть токов и напряжений — так называемых выходных величин f₂ , или реакций цепи на приложенные входные воздействия f₁, обусловленные дейст­вующими внешними независимыми источниками ЭДС и тока (рис.1). Такая постановка задачи носит название анализа по входу и выходу и является задачей основного анализа цепи.

В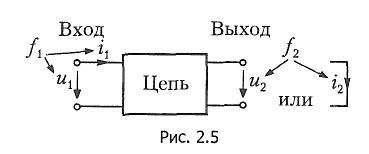 общем случае в цепи может действовать несколько входных источников и оп­ределяться несколько выходных величин. Однако наиболее часто при анализе определяют одну выходную величину f₂, обусловленную действием одного вход­ного источника f₁ (рис.1). В этом случае иногда сам источник на схеме цепи не изображают, а указывают лишь вызываемые им напряжение U₁ или ток I₁ на вхо­де цепи. Выходная величина также может быть напряжением U₂ на выходных за­жимах цепи или током I₂ в выделенной выходной ветви.

Обратной задачей анализа является задача синтеза цепи — опре­деление структуры и параметров элементов цепи, обеспечивающих заданный ха­рактер преобразования входного сигнала f₁ в выходной f ₂. Задача синтеза систем также является основной при проектировании систем, обеспечивающих те или иные рабочие функции в системах энергетики или информатики.

Для данного класса задач характерна возможность отсутствия решения — поставленные требования к закону преобразования сигнала могут оказаться не­реализуемыми. Поэтому отдельным этапом решения задачи синтеза является проверка условий реализуемости исходных данных. Следующей особенностью задач синтеза является неоднозначность их решения — полученное решение, как правило, оказывается не единственным, и при окончательном выборе оптималь­ного варианта приходится учитывать требования к проектируемому устройству, выходящие за рамки теории цепей (например, технологические или эксплуата­ционные).

К этому же типу относятся и задачи оптимизации цепей — определение парамет­ров элементов, при которых обеспечивается наилучшее в определенном смысле приближение к требуемым свойствам цепи или характеристикам преобразова­ния сигналов. Такие задачи обычно решают на основе сравнения результатов по­следовательно решаемых задач анализа цепи с изменяемыми параметрами. Этот путь перебора вариантов наряду с общей трудоемкостью решения вызывает осо­бые трудности при стремлении получить представление о разрешимости задачи синтеза, однозначности ее решения или достижимом приближении к идеально­му решению. Более эффективными являются специальные методы синтеза, раз­работанные для отдельных классов таких задач.

Иной характер имеет задача диагностики цепи — определение ее параметров по результатам измерений токов и напряжений на отдельных участках цепи. Она особо актуальна при исследовании сложных цепей с высоким уровнем интегра­ции элементов, когда полюса (зажимы) отдельных элементов недоступны для измерений. Задача диагностики не всегда имеет однозначное решение, поэтому она требует построения расчетной модели, позволяющей по результатам измере­ний токов и напряжений в частных режимах работы цепи (например, при подаче напряжения лишь на отдельные ее входы) получить' возможно более полное и точное описание цепи.

Дифференциальные уравнения системы.

Теория дифференциальных уравнений позволяет изучать всевозможные эволюционные процессы. Множество всевозможных состояний процесса называется фазовым пространством – пространством состояний.

Состояние любой, в частности, электрической системы часто удобно рассматривать в координатах «вход – выход» (рис.1)

Систему можно определить как совокупность (множество – группу) элементов, связанных между собой определенными зависимостями.

Элементы системы могут быть физическими (электрическими, механическими, термодинамическими и т. д.), химическими, биологическими или смешанными.

Для термина «вход системы» существуют различные выразительные названия, как причина, стимул, воздействие, возмущение, вынуждающая сила и т. д., а для термина «выход» - следствие, эффект, ответ, реакция и т. д.

Все эти названия указывают на то, что определенное изменение на входе системы влечет за собой некоторое определенное изменение на выходе системы. Зависимость выхода системы от ее входа определяется законом поведения системы, который может быть определен и экспериментальным путем.

В идеальном случае этот закон может быть выражен в виде математического уравнения, допускающего общее аналитическое решение. В такое уравнение входит некоторое число постоянных, или параметров, характеризующих определенные свойства системы.

Математический аппарат для анализа линейных дифференциаль­ных уравнений разработан достаточно полно и доведен до инженер­ного применения.

В общем виде дифференциальное уравнение (уравнение свободного движения) элемента (или систе­мы) может быть записано:

(1)

где Х_ВЫХ - выходная величина элемента или системы (для сокра­щения записи индекс времени в скобках здесь и далее опущен);

Хвх — входная величина элемента или системы;

a_i , b_i — коэффициенты, зависящие от конструктивных парамет­ров элемента или элементов системы.

В целях сокращения записи, введя оператор дифференцирования прямого преобразования Лапласа:

(2),

и вынося за скобки выходную и входную величины, дифференци­альное уравнение (1) можно записать в операторной форме (3):

(3)

Представляя выражения в скобках как многочлены от оператора р, диффе­ренциальное уравнение (3) можно сокращенно записать в виде отношения полиномов:

(4)

здесь полином m(p) - называется выходным оператором элемента или системы, а полином n(p) - входным оператором.

(5)

(6)

М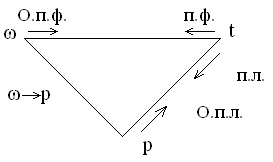 атематические методы получения системной функции электрических цепей, связаны с преобразованиями Фурье и Лапласа т.е. с переходом из временной в частотную область и область комплексного аргумента (рис. 2).

t → ω – (п. ф.) – Прямое преобразование Фурье (переход аргумента исследуемой функции из временной области в частотную область).

ω → t – (о. п. ф.) – Обратное преобразование Фурье (переход аргумента исследуемой функции из частотной области во временную область).

t

Рис.2

→ p – (п. л.) – преобразования Лапласа (переход аргумента исследуемой функции из временной в комплексную область).

p → t – (о. п. л.) – обратное преобразование Лапласа (из комплексной области во временную).

ω → p –замена аргументов ω на р (переход аргумента исследуемой функции из частотной в комплексную область; р – комплексное число).