17. Сложность. Подходы к определению сложности алгоритмов.

Аппарат машин Тьюринга позволяет изучить сложностные свойства алгоритмов. В информатике имеется несколько различных подходов к определению понятия сложности алгоритма. Например, понимают под сложностью число проверяемых логических условий. Каждое логическое условие определяет две различные ветки (пути) развития вычислительного процесса. Пусть число всех различных путей в программе есть N. Пусть p_i - вероятность прохождения программы по i-му пути.

Тогда мерой информационной сложности алгоритма (программы) считают энтропию Э, вычисляемую по формуле:

Информационная сложность характеризует возможность п о н я т ь работу алгоритма. Чем больше величина энтропии, тем больше усилий требуется, чтобы разобраться в логике программы. Однако для практики большее значение имеет не информационная, а алгоритмическая или вычислительная сложность алгоритма. Понятие алгоритмической сложности введено советским математиком А.Н.Колмогоровым. Под алгоритмической сложностью он понимал минимально необходимый размер программы для данного алгоритма. Колмогоров полагал, что чем меньше размер записи программы, тем меньше ее сложность. На этом пути ему и его коллегам удалось получить ряд ценных результатов. Вместе с тем оказывается, что даже небольшие по длине записи программы могут требовать огромного времени счета на ЭВМ и это время катастрофически растет с ростом размера входных данных.

Таким образом, выявляется необходимость ввести иную концепцию сложности – вычислительную сложность задачи и связать вычислительную сложность задачи с числом тактов, затрачиваемых машиной Тьюринга, реализующей алгоритм решения этой задачи за кратчайшее возможное число ходов.

Р.Карп обнаружил, что все задачи условно можно разделить на хорошо решаемые (эффективно решаемые) и плохо решаемые (неэффективно решаемые).

Р.Карп назвал все алгоритмы, которые требуют полином шагов от размера задачи эффективными или полиномиальными.

Однако есть задачи и алгоритмы вычислительная сложность которых растет быстрее любого полинома. Такие задачи называют плохо решаемыми, а алгоритмы неэффективными.

18. Алгоритмическая, информационная и инфологическая сложность.

Для изучения проблемы информационной сложности задач нужно прежде всего оговорить, какие задачи мы будем рассматривать. По очевидным причинам такие задачи должны быть в некотором смысле универсальными, т.е. к ним можно было бы сводить многие другие задачи из некоторого весьма широкого класса задач. Довольно часто в качестве такого класса задач выбирают задачи распознавания свойств, требующие только одного из двух ответов: «Да» или «НЕТ». Кроме того, требуют, чтобы решение задачи можно было эффективно проверить с помощью детерминированного алгоритма. Ранее мы рассматривали задачи сортировки и отмечали, что вычислительная сложность алгоритма сортировки определяется числом сравнений. Если это число растет как некоторый полином от размера исходного массива, то такой алгоритм называется эффективным. Обобщим это определение.

Детерминированный алгоритм называется эффективным, если число выполняемых им операций (не только сравнения) растет как некоторый полином от размера задачи. Под размером задачи понимают, вообще говоря, длину записи задачи при условии, что эта запись неизбыточна.

Итак, найти хорошее решение задачи – значит, построить для нее эффективный детерминированный алгоритм.

Назовем алгоритм недетерминированным, если, по крайней мере, на одном шаге, он допускает различные варианты продолжения работы и нет указаний, какой вариант выбрать.

Недетерминированный алгоритм называется эффективным, если его вычислительная ложность по любой из возможных трасс вычислений не превышает некоторого полинома от размера входной записи.

Так вот, под задачей распознавания свойств будем понимать задачу, такую, что:

1. она требует ответа «ДА» или «НЕТ»;

2. решение может быть проверено (если задача его действительно имеет) с помощью полиномиального (эффективного) недетерминированного алгоритма.

Рассмотрим задачу о выполнимости системы логических формул в форме дизъюнктов.

Дизъюнкт – это формула вида

,

(10.1)

где .

Примером дизъюнктов служат, например, следующие:

,

,

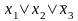и т.д.

Говорим, что дизъюнкт выполним в интерпретации , , если его значением в I служит «1».

Пример. Дизъюнкт выполним в интерпретации , так как .

Ясно, что число выполняющих интерпретаций для дизъюнкта, содержащего n переменных, составляет и в одной интерпретации он не выполняется.

Задача ВЫПОЛНИМОСТЬ требует дать ответ на вопрос: имеется ли интерпретация I, в которой выполняется каждый из дизъюнктов исходной системы.

Система дизъюнктов задачи Выполнимость называется также конъюнктивной нормальной формой. Среди всех конъюнктивных нормальных форм имеются формы с наименьшим числом дизъюнктов. Такие формы называются минимальными КНФ, эквивалентными данному множеству дизъюнктов.

Эта задача, очевидно, относится к числу задач распознавания. По смыслу вопроса она дает ответ «ДА» или «НЕТ». Если I – некоторая выполняющая интерпретация, то легко проверить (т.е. реализовать эффективный алгоритм проверки), что I выполняет каждый дизъюнкт системы. Эту проверку вполне можно осуществить с помощью детерминированного полиномиального алгоритма.

С. Кук доказал знаменитую теорему о том, что задача Выполнимость является универсальной в классе задач распознавания (этот класс получил короткое название NP (от слов Nondeterministic Polynomial)).

Итак, Выполнимость универсальна в NP. Однако, не смотря на более чем 100 летние усилия, не удалось найти для задачи Выполнимость эффективного детерминированного решающего алгоритма. Такая ситуация оказалась неслучайной. Сложность этой задачи оказывается большей, чем «пропускная способность» любого алгоритма, который был бы эффективным или детерминированным.

Остановимся на понятии пропускной способности канала связи, которые легко применить к вычислительной машине, решающей задачи.

Под пропускной способностью канала связи понимают величину

,

(10.2)

где H – энтропия системы до передачи сообщения;

H(S) – энтропия системы после передачи сообщения S;

T – время передачи.

Проще говоря, TH определяет, какое максимальное число бит информации в единицу времени может быть передано через канал связи. Очевидным образом следует признать, что эта величина имеет предел в силу конечности скорости света (во всяком случае, нам не известны в природе взаимодействия, протекающие с большей скоростью).