Министерство образования Республики Беларусь Учреждение образования

«Белорусский государственный университет информатики и радиоэлектроники»

А. В. Аксенчик			Р
		И
	У
Г
Б
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
а

вобластитинформатикие и радиоэлектроники

вкачестве учебно-ме одического пособия для студентов учреждений, обеспечивающихо получение высшего образованияспубликии

		л
	б
и
Б

Минск БГУИР 2011

УДК 519.2(075.8) ББК 22.17я73

А42

Ре це нзе нт ы:

кафедра высшей математики учреждения образования

«Белорусский государственный

аграрный технический университет», заведующий кафедрой,

кандидат физико-математических наук, доцент И. М. Морозова

доцент кафедры естественно-научных дисциплин

Р

И

учреждения образования «Белорусский национальный

технический университ», кандидат

У

физико-математических наук С. В. Чернявская

Г

Аксенчик, А. В.

Б

А42

Теория вероятностей и

а

матем тическ я статистика : учеб.-метод.

к

пособие / А. В. Аксенчик. – Минск : БГУИР, 2011. – 184 с. : ил.

ISBN 978-985-488-632-9.

ние

т

основ теории вероятностей и математиче-

Дается систематическое излож

ской статистики в соо ве с вии с

иповой учебной программой по данной дисцип-

лине.

Пособие сост ит из рех час ей. Часть 1 «Теория вероятностей» включает семь

и

глав, в которых рассм трены случайные события, случайные величины, предельные

теоремы. Часть 2 «Математическая статистика» содержит пять глав, где приведены

л

основные опреде еноя математической статистики, точечные и интервальные оцен-

ки, теория стат ст ческой проверки гипотез, линейный регрессионный анализ, а

б

также примеры решения задач. Часть 3 «Случайные процессы» выходит за рамки

и

уче ной программы, однако этот раздел будет полезен студентам радиотехнических

спец альностей при изучении специальных дисциплин, использующих основы тео-

Б

случайных процессов.

р

УДК 519.2(075.8)

ББК 22.17я73

ISBN 978-985-488-632-9

Аксенчик А. В., 2011

УО «Белорусский государственный

университет информатики

и радиоэлектроники», 2011

2

ПРЕДИСЛОВИЕ

Изучение основных положений теории вероятностей и математической статистики является важным элементом технического образования. Это обусловлено тем, что реальные физические процессы, при более глубоком их изучении, не описываются классическими методами математической физики, а требуют вероятностного подхода, т. е. неоднозначного описания физических явлений. Так возникли статистическая физика, квантовая механика. Непредска-

зуемый, случайный характер шумов, помех, статистическая структураРисточни-

ков сообщений, искажение радиосигналов при прохождении турбулентностей в атмосфере и ионосфере потребовали применения вероятностных методов в теоретической радиотехнике – так появилась статистическая радиотехника. И если

изучали студенты лишь некоторых специальностей, то в настоящееИвремя студенты большинства специальностей не могут обойтись без знания этой дисциплины.

в середине прошлого века теорию вероятностей и математическуюУ статистику

Основу данного учебно-методического пособия составляет курс лекций
по теории вероятностей, математической статистикеГи случайным процессам,
	а
который читался студентам второго курса радиотехнических специальностей
Белорусского государственного университета информатикиБ		и радиоэлектрони-
ки автором данного издания.	к

тами таких разделов курса высш й математики, как «Ряды», «Множества и

внимание в учебном пособии уделяется разъяснению основных определений и
руются на основных	понятиях теории множеств, на аксиоматическом подходе к
теорем теории вероятнос ей.
В части 1 «Те		вер я нос ей» (главы 1–7) данного пособия рассмот-
рия
рены все основные	пределеният, теоремы теории вероятностей, которые бази-
л
определению вероятности; все теоремы, свойства приводятся с доказательства-
операции над ними», «Диффер			и интегральное исчисления». Особое

Содержание учебно-методичеснциальноеого пособия предполагает знание студен-

ми. В главеб1 даются понятия о событиях, в главе 2 рассматривается определение случайнойи величины, формы законов описания распределений случайных вел ч н. В главе 3 содержатся сведения о многомерных случайных величинах. ЭтоБнесколько не традиционно, так как обычно после знакомства с одномерной случайной величиной рассматривают числовые характеристики случайных величин и их свойства. Однако не имея понятия о многомерных случайных величинах, привести доказательства свойств математического ожидания, дисперсии для суммы и произведения случайных величин не представляется возможным. Ввиду этого в третьей главе, для упрощения и лучшего понимания материала студентами, на примере двумерной случайной величины рассмотрены определения функции распределения и плотности распределения, а также приведены доказательства их свойств. Дано понятие общего определения математического ожидания, когда аргументом является функция случайной величины. Это об-

3

легчает запись выражения для определения дисперсии, начальных и центральных моментов случайных величин.

В части 2 «Математическая статистика» приведены основные понятия математической статистики, описаны методы получения точечных оценок параметров распределений. Рассмотрены основные законы распределений случайных величин, наиболее часто применяемых в математической статистике. Даны определения доверительной вероятности, доверительных интервалов для числовых характеристик. Изложена теория статистической проверки гипотез и

линейный регрессионный анализ.	Р
Включение третьей части в данное пособие вызвано тем, что ранее сту-

дентам радиотехнических специальностей разделы по случайным процессам читались, но в новой типовой программе они отсутствуют. Чтобы восполнить этот пробел, в пособие включена часть 3 «Случайные процессы» (глава 13) посвященная элементам теории случайных процессов. Даны основные понятия

теории случайных процессов, доказаны теоремы Винера-Хинчина, Котельнико-
ва, рассмотрены марковские случайные процессы.		И
Содержание 1-й и 2-й частей данного учебно-методического пособия
	У
полностью соответствует требованиям типовой учебной программы «Теория
	Г
вероятностей и математическая статистика», утвержденной Министерством об-

разования Республики Беларусь 03. 06. 2008, № ТДБ-1.030/тип., и предназначено для подготовки студентов широкого ряда специ льностей: 1-39 01 01 «Радио-

техника», 1-39 01 02 «Радиоэлектронные системыа», 1-39 01 03 «Радиоинформатика», 1-39 01 04 «Радиоэлектронная защита информации», 1-41 01 02 «Микро-

и наноэлектронные технологии и систкмы», 1-41 01 03 «Квантовые информа-

ционные системы», 1-39 02 01 «Моделирование и компьютерное проектирование радиоэлектронных средс в», 1-39 02 02 «Проектирование и производство

радиоэлектронных средство»,т1-36 04 01 «Электронно-оптические системы и технологии», 1-40 02 02 «Электр нные вычислительные средства» и др.

Часть 3 «Случайные пр цессы» данного учебно-методического пособия может использоваться для подготовки студентов следующих специальностей:

1-39 01 01 «Радиотехн ка», 1-39 01			02 «Радиоэлектронные системы», 1-39 01 03
б	и		«Радиоэлектронная защита информации»,
«Радиоинформатика», 1-39 01 04
1-40 02 02 «Электронныел		вычислительные средства».
Данное уче но-методическое пособие может быть использовано для под-

готовкиБистудентов высших и средних специальных учебных заведений по экономическим и другим специальностям.

4

ЧАСТЬ 1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ

ГЛАВА 1. СЛУЧАЙНЫЕ СОБЫТИЯ			Р
1.1. Основные понятия теории вероятностей
		И
Теория вероятностей – это математическая наука, которая изучает зако-
номерности случайных явлений.	У
	Г
До возникновения теории вероятностей объектом исследования науки

были явления или эксперименты, в которых условияБпостановки эксперимента однозначно определяли его исход. В этом случ е результат эксперимента может

быть рассчитан заранее с использованиемасоответствующих законов физики.

Эксперименты, результаты оторых можно предвидеть заранее, ис-

пользуя естественно-научные законы и выполняя соответствующие условия
его проведения, называются д							к
						рминированными.
Примером детерминированногоеэксперимента является определение силы
				о
постоянного тока I через пр водник по известному сопротивлению R провод-
			ением		т			I	U
									R (используется закон Ома). Здесь
ника и падению напряжения U						на нем:
		л
искомая ве ичина I однозначно определяется условиями проведения экспери-
	б			R и напряжением U).
мента (сопротив
Однако ус овия, при которых проводится эксперимент, часто бывает
и
трудно сделать фиксированными. И это может приводить к разным результатам.
Б								режима электрической схемы какого-
Напр мер, если проводить измерение

либо устройства, собранного на печатной плате, то результаты измерений могут зависеть от разных факторов: входного сопротивления вольтметра (если цепи высокоомные, то происходит шунтирование их входным сопротивлением вольтметра, изменяется режим работы схемы, и это влияет на результаты измерений); температуры, влажности в помещении, где находится устройство (при повышенной влажности возникают токи утечки между печатными проводниками, особенно заметно их влияние в высокоомных цепях, и результаты измерений изменяются); напряжения сети (известно, что в жилых многоэтажных домах утром и днем напряжение сети повышенное – 240–250 В, а вечером пони-

5

жается – 215–230 В, т. к. люди приходят с работы включают различные потребители электрической энергии, нагрузка (ток) в сети возрастает и на подводящих электричество к дому кабелях увеличивается падение напряжения, что приводит к уменьшению напряжения на розетках в квартирах). Здесь, как видим, проявляется зависимость напряжения сети и от времени суток. Отметим, что, несмотря на то что для питания электронных схем используют стабилизаторы напряжения, не все они могут поддерживать стабильное напряжение, если напряжение сети меняется в широких пределах. Поэтому часто в документации

на электронные устройства указывают условия измерения режима работы схе-
	Р
мы устройства: напряжение сети, температура, влажность, входное сопротив-
ление вольтметра.	И
Однако условия, при которых проводится эксперимент, трудно сделать

фиксированными, и даже незначительное их изменение приводит к другому ре-
		У
зультату. Поэтому в отличие от детерминированных можно выделить другой
класс экспериментов – вероятностные.	Г
Вероятностные эксперименты (стохастические или случайные) – это
	Б
эксперименты, которые при соблюдении одних и тех же (насколько это воз-

можно) фиксированных условий можно повторять произвольное количество раз, каждый раз, но исход вероятностного эксперимента будет неоднозначен, случаен.

дая одни и те же (насколько это возможноа) фиксированные условия, можно заметить, что совокупность исходов та их э спериментов все же подчиняется оп-

ределенным закономерностям. Изуч никм этих закономерностей, а точнее их

Но при многократном повторении вероятностного эксперимента, соблю-

математических моделей, и занимается т ория вероятностей. Приведем примеры вероятностных эксперимен ов.

минимальная и максимальнаяотвысоты, выходить за пределы которых он не должен. Теоретически н д лжен лететь горизонтально, прямолинейно, равномерно на заданной высоте (середина коридора). Однако при полете на заданной

1. Самолету для п ле а на определенной высоте отводится коридор –

высоте на само ет воздействуют вертикальные и горизонтальные потоки воз-
		и
	полета
б
духа, т. е. влияет турбу ентность атмосферы. Это вызывает отклонение центра
и			по горизонтальной прямой и приводит к колебаниям
масс самолета от

самолета около центра масс. Поэтому здесь высота, направление и скорость полетаБне определяются однозначно, а являются случайными и изменяются от полета к полету.

2. Пусть проводится эксперимент с броском симметричной монеты. В результате возможны два взаимоисключающих друг друга исхода: выпадает герб или цифра. Если бы мы точно знали начальные условия данного эксперимента (скорость вращения, скорость поступательного движения, начальное положение монеты в момент броска), то мы смогли бы предвидеть исход этого эксперимента (т. е. точно рассчитать). Однако начальные условия трудно сделать фиксированными, и незначительное изменение их приводит к другому результату. Тем не менее если мы будем проводить такой опыт многократно, то

6

совокупное число его исходов будет подчиняться определенным закономерностям: число выпадений герба числу выпадений цифры (в том случае, если монета симметричная).

3. В городе возникла эпидемия гриппа. Человек, заболевший гриппом в этот период, может выздороветь; получить осложнения различной степени тяжести; а может и умереть. Видим, что исход заболевания гриппом непредсказуем.

4. Предположим, что проводим измерения некоторой величины (измерение напряженности электромагнитного поля телевизионного сигнала в ка-

кой-либо точке города, дальности радиолокатором и т. д.). Заранее предвидеть результат трудно. Однако при аккуратном проведении измеренийРи после многократного их повторения наблюдается закономерность: среднее арифметическое результатов измерений приближается к некоторой постояннойИвеличине.

Можно найти приближенное значение данной константы и, построив математическую модель эксперимента, с определенной степенью уверенности принять эту оценку за реальное значение измеряемой величины.

Следует также отметить, что теория вероятностей занимается изучением

не любых случайных событий, а только тех, которые обладают определенными
	У
Г
Б
свойствами. Во-первых, таких, которые при фиксированных условиях могут
осуществляться произвольное число раз, например – бросок монеты, бросок иг-

ральной кости. Во-вторых, таких, которыеаобл д ют статистической устойчивостью. Например, сделаем n бросков монеты (испытания) и будем следить за появлением герба (событие А). Пусть эти испыт ния проводятся в одинаковых условиях и каждое испытание не о азывает влияния на остальные, т. е. они яв-

ляются независимыми. Пусть	А появится при n испытаниях m раз. То-
	к
гда относительная частота появл ния события А, обозначим ее Р*(А), будет
определяться как Р*(А) = m/n. Проводясобытиетакой опыт, мы можем заметить, что при

большом n относительная час о а Р*(А) близка к какой-то постоянной и лишь
	т
незначительно меняется в различных сериях из n испытаний. В дальнейшем мы
покажем, что ч сло, к	к торого колеблется относительная частота, и есть
не что иное, как вероятностьло		события А – Р(А). Заметим, что относительная

частота появ лен ия событ я А может быть определена только после проведения опыта (когда становится известным число m), а вероятность Р(А) может быть рассчитана и до опыта. Из приведенных примеров логически следует определе-

ние вероятностиб – как меры возможности наступления какого-либо события при проведен и вероятностного эксперимента. Это не точное определение ве-

роятностиБи(его мы рассмотрим позже при изучении аксиом), но смысл передается верно.

Таким образом, мы видим, что понятие вероятностного эксперимента достаточно широко, однако можно выделить следующие общие черты:

1)множество возможных исходов;

2)непредвиденность результата;

3)наличие определенных количественных закономерностей при многократном повторении эксперимента.

7

Эти закономерности изучаются методом моделирования. Для этого строится математическая модель вероятностного эксперимента, в котором исследуемые закономерности описываются различными математическими уравнениями, функциями. Насколько точна математическая модель и хорошо ли она согласуется с практикой, можно вычислить с помощью методов математической статистики. Таким образом, предметом теории вероятностей является количественный и качественный анализ математических моделей вероятностных экспериментов. Эксперименты проводят с целью получения научных вы-

водов, рекомендаций, на основе которых можно принимать решения.

работах Дж. Кардано (1501–1575), Х. Гюйгенса (1629–1695), Б. ПаскаляР(1623– 1662), П. Ферма (1601–1665) и др. в ХVI – ХVII вв. Следующий этап развития

Первые работы, в которых зарождались основные понятия теории веро-

ятностей, представляли собой попытки создания теории азартных игр. Именно

теории вероятностей связан с именем Якова Бернулли (1654–1705)И. Доказанная им теорема, получившая впоследствии название «Закон больших чисел», была

они стимулировали построение математических моделей игровых ситуаций в

первым теоретическим обоснованием накопленных ранееГУфактов. Дальнейшими успехами теория вероятностей обязана П. Д. ернулли (1700–1782), П. Лап-

наиболее плодотворный период связан с имен миБП. Л. Чебышева (1821–1894) и его учеников А. А. Маркова (1856–1922) и А. М. Ляпунова(1857–1918). Со-

ласу (1749–1827), К. Гауссу (1777–1855), С. Пуассону (1781–1840) и др. Новый

временная теория вероятностей получилаар звитие в работах С. Н. Бернштейна, А. Н. Колмогорова (1903–1987), Б. В. Гн д н о и др. Однако строгой математи-

ческой наукой теорию вероятносткй сделала работа русского ученого

А. Н. Колмогорова «Основные понятияет ории вероятностей», опубликованная в 1933 г. В этой работе А. Н. Колмогоров сформулировал аксиомы теории вероятностей и для доказательс ва основных положений применил теорию мно-

жеств.				т
	1.2. Пространствоо				элементарных событий
		и
Рассмотрим простые примеры.
1. Под расываниел			игральной кости один раз. В результате этого опыта
	б
	и				k

могут наступ ть различные события: выпали 2, 6, 5… очков, число выпавших

очков четно т. д. Мы будем различать элементарные (неразложимые) собы-
тия, составные события или просто события. Обозначим		– событие со-

стоит в том, что выпадает k очков. Элементарными событиями в данном опыте
Б	,	2	, ,...,	6 . Составные события или просто события могут быть
являются:	1		3
описаны	как		подмножества		множества	элементарных	событий

1 , 2, 3,..., 6 . Так событие А = {выпало четное число очков} через элементарные события выражается следующим образом : A { 2, 4, 6}.

8

2.Трехкратное подбрасывание монеты. При каждом подбрасывании будем записывать результат опыта, обозначая выпадение герба – «1», а цифры – «0» (010 – при втором подбрасывании выпал герб). Множество элементарных событий состоит из 8 элементарных событий:

{000, 001, 010, 011,100,101,111} или { 1, 2,..., 8}. А = {при первом подбра-

сывании выпал герб} является составным: A {100, 101, 110, 111} . Любое подмножество множества можно интерпретировать как некоторое событие реального опыта. Например, событие В = {110, 101, 011} состоит в том, что вы-

пало ровно 2 герба.	Р

3.Семья с тремя детьми. Для того чтобы изучить распределение мальчи-

Тройка ДММ представляет следующий исход: старший ребенокИ– девочка,

ков и девочек во всех семьях, имеющих трех детей, составлен список этих семей. Какое пространство событий отвечает эксперименту, заключающемуся в

		У
выборе одной семьи? Множество элементарных событий состоит из 8 эле-
ментарных событий		= {МММ, ММД, МДН, МДД, ДММ, ДМД, ДДМ, ДДД}.
		Г

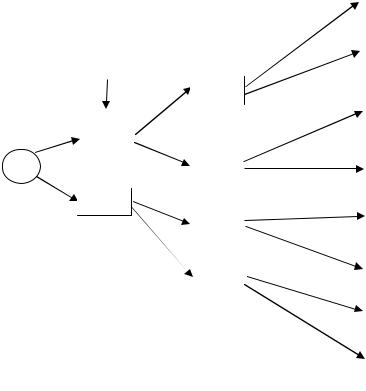
средний и младший – мальчики. Задача легко решается, если построить «дере-

во» эксперимента (рис. 1.1).

Б

а

М

к

Первый ребенок

Д

е

М

Д

т

М

М

о

Д

Д

и

М

л

М

б

Д

Д

и

М

Б

Второй

Д

ребенок

Третий ребенок

Рис. 1.1

Таким образом, можно дать следующие определения:

9

1. Элементарным событием называется любой мысленно возможный результат эксперимента. Совокупность всех элементарных событий образует некоторое множество .

2.Пространством элементарных событий будем называть множество

{ } всех мыслимых, взаимоисключающих друг друга исходов опыта или эксперимента.

По числу элементов пространство элементарных событий может быть конечным, счетным. Пространство с конечным множеством элементов

1.3.Операции над событиямиБГУИР

1.Случайным событием или простоасобытием назовем любое под-

множество множества . События будемкобозн чать заглавными буквами ла-не

примеров следует, что случайным событи м называется всякий факт, который в

результате опыта может произой и или произойти. Если А влечет В, а В вле-
чет А ( A B , а B A ), А и В происходят лишь одновременно (А = В),
множества А и В совпадают, и г	, что А равносильно или тождественно В.
ворят
2. Достоверным с бытием	называется событие, совпадающее с про-
о	. Если записать A , то А – досто-
странством э ементарных событий

верное событие. Достоверное событие происходит при каждом повторении экс-
		и
перимента (опыта).
3.	л		называется событие, совпадающее с пус-
	Невозможным событием
тым множеством. Если записать А =				, тогда А является невозможным собы-
	б
тием. Невозможное событие не появится ни в одном из исходов вероятностного
экспериментаи.
Б

Aназывается дополнение множества

Ат. е. событие A состоит из таких элементарных событий, которые не4. Противоположным событиемдо ,

входят в событие А: A { | A}. Противоположное событие A происходит тогда, когда событие А не происходит. Например, при броске игральной кости

10

событие

A – нечетное число очков. A { 1, 3, 5} является противоположным

событию A { 2, 4, 6}.

Очевидно,

что , A A. Для иллюстрации операций над событиями

удобно использовать диаграмму Венна (рис. 1.2).

1

принадлежит событию А,

1 A;

2

2

не принадлежит событию А,

2 A.

А

Справедливы соотношения:

Р

A A,

, .

1

A

Рис. 1.2

И

5.

Объединением или суммой двух событий А и В называют событие,

У

содержащее те элементарные события , которые принадлежат или собы-

тию А, или событию В, или А и В. Объединение илиГсумму двух событий будем

обозначать

A B (рис. 1.3):

Б

В,

или

А и В}.

A B { | A, или

Для

любого события А справедливы

а

В

сл дующие соотношения:

А

к

= A

, A .

A A A , A

А В

е

Рис. 1.3

т

6.

о

В называется со-

Пересечен ем

ли произведением двух событий А и

бытие, состоящее

тех элементарных событий , которые принадлежат

и событию А, и

из

событию В одновременно или совместно. Пересечение или

л

произведение двух событий будем обо-

б

значать AB A B. Согласно определению

A B { | A, B}.

и

Справедливы следующие соотношения:

Б

В

A A A, A = , A A.

А

А В

Рис. 1.4

11

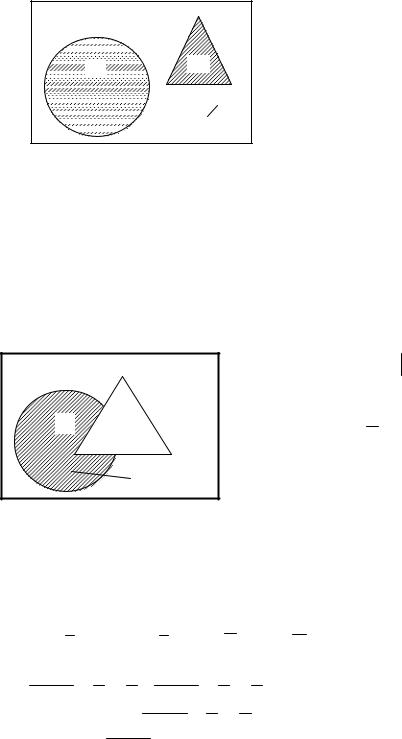
Отметим, что выделенные слова или в определении для суммы, а также и

в определении для произведения позволяют легко сориентироваться, какую

операцию следует применить между событиями.

7.

События A и B называются несовместными, если их пересечение яв-

ляется невозможным событием, т. е. если A B= . Для несовместных собы-

тий одновременное наступление в одном опыте невозможно.

А

В

Р

А В=О

Рис. 1.5

И

У

Отметим, что элементарные события являются несовместными, т. к. при

i j, i

j .

Г

8.

Разностью двух событий А и В н зыв ется событие, состоящее из тех

Б

элементарных событий , которые входят в событие А, но не входят в со-

бытие В (рис. 1.6).

Разность

будем

обозначать:

Aк\ B: A\ B A, но В .

е

Разность

событий

можно выразить

ранее

введенные

операции:

А

В

т

через

A\ B A B.

А\В

о

Рис. 1.6

и

л

б

Основные законы алгебры событий.

Для алгебры событий справедливы следующие законы:

аи) дополнения:

A

A ;

A A ;

; =

;

Б

принцип двойственности:

A B A B; A B A B.

Докажем, что A B A B.

Событие A B состоит в том, что не происходит событие A B , состоящее в наступлении хотя бы одного из событий А или В (согласно пункту 5).

12

Но это буквально и означает, что не происходит ни событие А, ни В, т. е., со-

гласно пунктам 4 и 7, происходит A B, значит, A B A B. Наоборот, если происходит A B, то не происходит ни А ни В, следовательно не происходит событие A B, т. е. происходит A B , следовательно, A B A B , а

значит, A B A B. Кратко можно описать так:

( A B A B A, B A, B A B ),

здесь означает эквивалентно.

б) коммутативности:

A B B A

Р

A B B A

в) ассоциативности:

(A B) C A (B C)

(A B) C A (B C)

И

г) дистрибутивности:

A (B C) (A B) (A C)

У

A (B C) (A B) (A C)

Г

Если последнее соотношение очевидно, то первое можно доказать так

(начнем с правой части):

Б

(A

учтем: A A A

B) (A C) A A A C B A B C

A A C B A B C

представим A A

а

к

(A A C A B) B C

применимзаконассоциативности

A ( C B) B C

уч

: C B

A (B C).

ем

Для удобства записей в еории вероятностей можно опускать символ пе-

ресечения , т. е.

ABC

вместо

A B C или A B вместо A B.

т

1.4. Аксиомы теоровероятностей (Аксиомы Колмогорова А. Н.)

пишется

Рассмотренные ранее свойства операций над событиями носят алгебраи-

ческий характер. В теории вероятностей для некоторого класса подмножеств F

л

ввод тся понятие алгебры событий. Класс подмножеств F всех возможных со-

быт й вероятностногоб

эксперимента должен удовлетворять следующим усло-

виям.

и

В из таких событий, как A Fи B F,

1.

Для каждой пары событий А и

следует,

что A B F . Иными словами, класс F вместе с каждой парой собы-

Б

тий содержит их объединение.

2.

Вместе с каждым событием А класс F содержит противоположное

событие

. Если класс F не пуст, то F ,

т. к. A

.

Следовательно,

A

A

F ,

поскольку =

. Наконец,

согласно принципу

двойственности,

, класс F содержит их пересечение

A B и разность A\B A

.

A B

A

B

B

13

Класс подмножеств F, удовлетворяющий условиям 1 и 2, называется алгеброй событий.

Конструкция алгебры событий позволяет охарактеризовать множество всех возможных результатов любого эксперимента со случайным исходом, если множество его элементарных исходов конечно. Например, в эксперименте с игральной костью состоит из шести элементарных событий, а F состоит из всех подмножеств . F содержит пустое множество , 6 = С61 – одноточечных подмножеств, 15 = С62 – двухточечных подмножеств и т. д. Значит F содержит

26 = 1+ С61 + С62+…+ С66 = 64 события.

Если

состоит из

n

элементарных

событий,

то

F состоит из

2n Cn0 Cn1 ... Cnn событий. Если | | n, то |F| 2n .

Ниже

перечислены

аксиомы

теории

вероятностей

(или аксиомы

А. Н. Колмогорова).

Р

1. F является -алгеброй событий. Алгебра событийИF называется

-алгеброй,

если для каждой

счетной последовательности событий Aj F ,

У

такжеГпринадлежит F, т. е.

j = 1, 2,…, их объединение B A1 A2

... Aj

1

Б

1

а

является событием. Согласно принципу двойственности, отсюда следует, что и

C

Aj

F

к

. Действительно,

C

A

A

... A A ...

. Следует под-

1

2

1

2

черкнуть,

е

что речь идет лишь о сч тных объединениях и пересечениях. Если

A ,

S

–

произвольная

т

то,

например,

их объединение

сис

ма событий,

A может и не быть

собы

ием.

S

Первая акс ома вв д

п нятие -алгебры событий. Можно отметить,

л

что -алгебра событ й – это расширение понятия алгебры событий на беско-

нечную последовате ьность событий.

2.

На -а гебреиF определяется функция Р( ), принимающая числовые

значения P(A) 0д я A F, называемая вероятностью и обладающая свойст-

и

вами, которые описывают нижеследующие аксиомы.

Б

Отметбм, что вторая аксиома вводит понятие вероятности.

3.

Для всяких двух событий А и В, при которых A B , т. е. несовме-

стных, P(A B) P(A) P(B) –

аксиома сложения вероятностей для несо-

вместных событий (аксиома конечной аддитивности). Для произвольного конечного числа несовместных событий

P(A1 A2 ... An) P(A1) P(A2) ... P(An).

4. Пусть Aj, j 1, 2,...	–	попарно несовместны: Ai Aj ,	если
i j; i, j 1,2,... и A A1 A2	...,	тогда P(A) P(A1) P(A2) ... P(Ai )	(за-
		i 1

14

метим, что, согласно аксиоме 1, A F). Эта аксиома определяет счетную ад-

дитивность вероятности, иногда ее называют аксиомой непрерывности вероятности.

Здесь следует сделать некоторые пояснения. Напомним, что аддитивные величины – это величины, связанные с геометрическими или физическими объектами таким образом, что величина, соответствующая целому объекту, равна сумме соответствующих его частей, каким бы образом мы не разбивали объект на части. Поэтому площади, объемы, массы тел удовлетворяют условиям адди-

тивности (аксиомам) и их можно принимать за меры тел. Диаметры, например,
	Р
не удовлетворяют условиям аддитивности и за меру приняты быть не могут.
5. P( ) 1 – аксиома нормировки.	И
Числовую функцию Р(А), как мы отмечали, называют вероятностью или

вероятностной мерой появления события А, и из аксиом следует, что вероят-

ность любого события А: 0 P(A) 1.

У

Пространство элементарных событий ,

выделенная -алгебра собы-

тий F и определенная на измеримом пространстве ( ,F) вероятностная мера

Р появления события A

Б

которое

Fобразуют вероятностное пространство,

принято обозначать ( ,F,P).

Г

Вероятностное пространство ( ,F,P) совместно с аксиомами представ-

ляет собой математическую модель вероятностного эксперимента.

Рассмотрим следующий эксперимент: в коробке находятся три шара раз-

е

ных цветов – белый, черный, красный. Неаглядя, вытаскиваем один шар.

, }

Пространство элементарных событий этого эксперимента { ,

к

1

2

3

и состоит из трех исходов, где 1 – {достали шар

белого цвета}, 2 – {достали

1

2

3

чество1 2

1 3

2

3

1

2

шар черного цвета),

3

– {дос али шар красного цвета). Выделим в качестве

-алгебры событий F э

го эксперимента

систему всех подмножеств (ранее

стоит в том, что

вытащили или белый, или черный шар; { 1

, 3} –

состоит в том,

мы отметили, что к л

тподмножеств в F должно быть равно

F 23

8):

л

Здесь событие

{ , }

со-

F { ,{ },{ },{ },{ , },{ , },{ , }, }.

б

что вытащи и и и бе ый, или красный шар; { 2, 3} состоит в том, что выта-

ли

1

2

3

1

2

щили

черный, или красный шар;

Б

Определим для этих событий вероятностную меру P:

P( ) 0;

P( ) 1/3; P( ) 1/3;

P( ) 1/3;

P( , ) 2/3;

P( 1, 3) 2/3;

P( 2, 3) 2/3; P( ) 1.

Определенная таким образом функция Р(А) удовлетворяет аксиомам

Колмогорова

( 1 2 3;

P( ) P( 1) P( 2) P( 3) 1; 1 2 3 ),

15