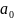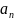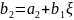- •Приближенные методы вычисления значений функции
- •Решение систем линейных уравнений
- •Метод итерации решения систем линейных уравнений
- •Метод Зейделя
- •Приближенные методы решения алгебраических и трансцендентных уравнений
- •Отделение корней, т.Е. Установление возможно тесных промежутков, в которых содержится один и только один корень уравнения.
- •Метод хорд решения уравнений
- •Метод касательных решения уравнений
- •Метод итерации решения уравнений
- •Метод итераций решения системы двух уравнений
- •Метод Лобачевского-Греффе решения алгебраических уравнений
- •Интерполирование функций
- •Первая интерполяционная формула Ньютона
- •Вторая интерполяционная формула Ньютона
- •4.3 Интерполяционная формула Стирлинга
- •4.4 Интерполяционная формула Лагранжа
- •Численное интегрирование
- •Формулы трапеций и парабол вычисления определенных интегралов функций одной переменной
- •5.1.2 Метод парабол
- •Экстраполяция по Ричардсону
Оглавление
1. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ЗНАЧЕНИЙ ФУНКЦИИ 1
1.1 Схема Горнера вычисления значений функции, заданной в виде многочлена 1
1.2 Метод итерации вычисления значений функции 2
1.2.1 Вычисление обратной величины 2
1.2.2 Вычисление квадратного корня 2
1.2.3 Вычисление обратной величины квадратного корня 2
1.2.4 Вычисление кубического корня 2
2. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ 2
2.1 Метод итерации решения систем линейных уравнений 3
2.2 Метод Зейделя 4
3 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ 5
3.1 Отделение корней, т.е. установление возможно тесных промежутков, в которых содержится один и только один корень уравнения. 5
3.2 Метод хорд решения уравнений 5
3.3 Метод касательных решения уравнений 5
3.4 Метод итерации решения уравнений 6
3.5 Метод итераций решения системы двух уравнений 6
3.6 Метод Лобачевского-Греффе решения алгебраических уравнений 7
4 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ 8
4.1 Первая интерполяционная формула Ньютона 8
4.2 Вторая интерполяционная формула Ньютона 8
4.3 Интерполяционная формула Стирлинга 9
4.4 Интерполяционная формула Лагранжа 9
4.5 Применение интерполяционных формул при дифференцировании функций одной переменной 10
4.5.1 Для первой формулы Ньютона: 10
4.5.2 Для формулы Стирлинга 10
4.5.3 Для второй формулы Ньютона 10
5. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ 11
5.1 Формулы трапеций и парабол вычисления определенных интегралов функций одной переменной 11
5.1.1 Метод трапеций: 11
5.1.2 Метод парабол 12
5.2 Экстраполяция по Ричардсону 12
Приближенные методы вычисления значений функции
1.1 Схема Горнера вычисления значений функции, заданной в виде многочлена
Теорема
1.
Числа
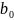 ,
,
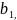 ...,
...,
 являются
коэффициентами
полинома Q(x),
полученного
в качестве частного при делении полинома
f(x)
на
двучлен х
-
являются
коэффициентами
полинома Q(x),
полученного
в качестве частного при делении полинома
f(x)
на
двучлен х
-
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
1.2 Метод итерации вычисления значений функции
Формула:
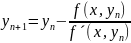
Сходимость процесса будет обеспечена., если первая и вторая производная сохраняют постоянные знаки в интервале, содержащем корень у.
1.2.1 Вычисление обратной величины
Формула:

Вычисление
начального значения
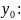
Представляем
x
как x=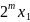 ,
где m-целое
число и
,
где m-целое
число и
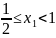 .
Тогда полагают
.
Тогда полагают
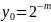
1.2.2 Вычисление квадратного корня
Формула:
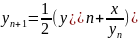
Начальное приближение такое же, но
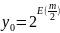 (
(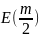 -целая
часть
-целая
часть
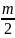 )
)
1.2.3 Вычисление обратной величины квадратного корня
Формула:

Начальное приближение

1.2.4 Вычисление кубического корня
Формула:
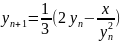
Начальное приближение

Решение систем линейных уравнений
Способы решения систем линейных уравнений (СЛУ) делятся на две группы: точные методы и итерационные методы. Под точными методами понимают конечные алгоритмы для вычисления корней системы (например, правило Крамера, метод Гаусса, метод главных элементов и т.д.). Итерационные методы позволяют получать корни системы с заданной точностью путем сходящихся бесконечных процессов (например, метод итерации, метод Зейделя и т.д.).
Метод итерации решения систем линейных уравнений
Дана система:
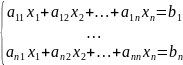
Для решения необходимо:
Вынести x из каждого уравнения за знак равенства
Заменить
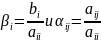 при
i<>j
при
i<>j
(Получим
следующее выражение : x=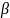 +
+ x)
x)
Произвести процесс итерации по формуле.
Формула:
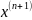 =
= (
(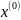 =
)
=
)
Теорема
1.
Если
последовательность приближений
,
… ,
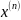 ... имеет
предел
... имеет
предел
х = lim ,
то этот предел является решением системы, при этом говорят, что процесс итерации сходится.
Определение
1.
Нормой
матрицы А
= [ ]
называется
действительное число
||А||, удовлетворяющее
условиям
]
называется
действительное число
||А||, удовлетворяющее
условиям
||А|| ≥ 0, причем ||А|| = 0 <=> А = 0
|| А|| = ||А|| , — число
||А + В|| ≤ ||А|| + ||В||
||АВ|| ≤ ||А|| + ||В||
Определение 2. Норма матрицы А = [ ] называется канонической, если выполняются дополнительные сл. условия:
| | ≤ М,
из неравенств |А| ≤ |В| следует неравенство ||А|| ≤ ||В||.
Виды норм:
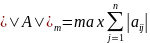
 =
=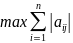
Теорема 2. (Достаточное условие сходимости процесса итерации) Процесс итерации для приведенной линейной системы сходится к единственному ее решению, независимо от выбора начального приближения, если какая-нибудь каноническая норма матрицы а меньше единицы.
Теорема 3. (Оценка погрешности принижений процесса итерации) Если за к обозначить число итераций, то норма погрешности к-той итерации
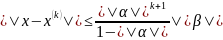
Пример таблицы:
|
х1 |
х2 |
х3 |
х4 |
0 |
2.1500 |
-0,8300 |
1,1600 |
0,4400 |
1 |
2,9719 |
-1,0775 |
1,5093 |
-0,4326 |
2 |
3,3555 |
-1,0721 |
1,5075 |
-0,7317 |
3 |
3,5017 |
-1,0106 |
1,5015 |
-0,8111 |
4 |
3,5511 |
-0,9783 |
1,4944 |
-0,8321 |
5 |
3,5662 |
-0,9644 |
1,4910 |
-0,8364 |
6 |
3,5703 |
-0,9593 |
1,4896 |
-0.8368 |
7 |
3,5713 |
-0,9576 |
1.4891 |
-0.8367 |
8 |
3,5714 |
-0.9571 |
1.4889 |
-0.8365 |
9 |
3,5714 |
-0,9570 |
1,4889 |
-0,8364 |
10 |
3,5714 |
-0,9570 |
1,4889 |
-0,8364 |