24.Другие np-полные задачи. Примеры сводимости в классе np

Определение. Задача А эффективно сводится к задаче В, если

1. Решение задачи B дает решение задачи А;

2. Сложность сведения ограничена полиномиальной функцией.

Примеры сведений.

Задача ВЫПОЛНИМОСТЬ эффективно сводится к задаче 3-ВЫПОЛНИМОСТЬ. Задача 3-ВЫПОЛНИМОСТЬ – это задача ВЫПОЛНИМОСТЬ, каждый дизъюнкт которой содержит не более 3-ех переменных. Рассмотрим на пример, как эта сводимость реализована.

Пусть дана система дизъюнктов

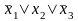
S=

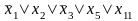
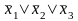
Здесь только второй дизъюнкт содержит более 3 переменных. Заменим второй дизъюнкт, как показано ниже:

S1=

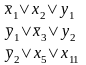
Можно усмотреть следующий общий прием. Мы вводим дополнительную переменную в каждый дизъюнкт, содержащий более трех переменных. Затем отсчитываем три литеры и переносим оставшиеся переменные в новый дизъюнкт. В перенесенном дизъюнкте мы добавляем новую литеру, но уже с отрицанием и т.д.

Задание 6. Доказать, что системы S и S1 эквивалентны.

Указание. Доказательство можно провести с помощью таблицы истинности. Для этого следует ввести понятие таблицы истинности. В нашем случае такую таблицу следует заметно укоротить до

y1	y2
0	0
0	1
1	0
1	1

Возьмем любую строчку из этой таблицы и подставим ее в S1. Ясно, что из выполнимости полученной новой системы автоматически будет следовать выполнимость системы S.

Наоборот, допустим, что система S выполнима, а S1 – невыполнима. Это значит, что как минимум один дизъюнкт в S1 не выполним. Такой дизъюнкт всегда содержит хотя бы одну новую переменную. Дадим этой переменной значение 1. По этому способу можно добраться до последнего дизъюнкта. Завершите эту схему рассуждений.

Задача о паросочетаниях сводится к задаче ВЫПОЛНИМОСТЬ.

Пусть имеется 5 девушек a,b,c,d,e и пять парней x,y,z,w,u. В следующей матрице 1 на пересечении строки i и столбца j означает взаимную симпатию, а 0 – в лучшем случае безразличие. Следует подобрать 5 пар, взаимно симпатизирующих друг другу.

	a	b	c	d	e
X	1		1
Z		1			1
Y	1			1
U			1	1
W		1			1

25.Метод резолюций Робинсона для задачи выполнимость.

Напомним, что задача ВЫПОЛНИМОСТЬ требует установить, имеется ли для данной системы дизъюнктов общая выполняющая интерпретация. Напомним также, что примерами дизъюнктов являются следующие:

и т.д.

Здесь х_i являются булевскими переменными. Булевская переменная может принимать только два значения: 0, 1. Черта сверху над переменной означает ее отрицание. Правила отрицания таковы:

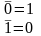
Значок v называется операцией логическое “ИЛИ” (а также дизъюнкцией). Эта операция дает в результате единицу, если и только если хотя бы одна из участвующих в ней переменных равна 1.

Задача ВЫПОЛНИМОСТЬ заключается в следующем. Имеется множество дизъюнктов. Спрашивается, имеется ли для этого множества дизъюнктов хотя бы одна общая выполняющая интерпретация? Если ДА, то множество дизъюнктов называется выполнимым. Если НЕТ, то множество дизъюнктов называется невыполнимым. Эта задача имеет только кажущуюся простоту. На самом деле, проблема упирается в отыскание эффективного алгоритма ее решения, которую мы рассматриваем на следующем практическом занятии.

Принцип резолюций. Принцип резолюций заключается в систематическом построении следствий из текущей системы дизъюнктов на основе операции резолюционирования. Следствия называются резольвентами. Резольвенты строятся для пары дизъюнктов, содержащей контрарную пару литер (булевских переменных). Например, пусть даны два дизъюнкта

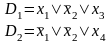
Эти дизъюнкты содержат контрарную пару литер - (одна входит в дизъюнкт D₁ без отрицания, вторая – в дизъюнкт D₂ с отрицанием).

Резольвентой дизъюнктов D₁ и D₂ является новый дизъюнкт D_1,2 , который не содержит контрарной пары литер, но содержит все другие литеры из D₁ и D₂. Согласно этому определению, получим D_1,2= .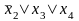

Целью построения резольвент является достижение следующих возможных исходов:

• Резольвента оказалась пустой. Например, пустую резольвенту дает следующая пара дизъюнктов

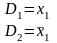
В случае пустой резольвенты делается вывод о невыполнимости системы дизъюнктов (т.е. задача ВЫПОЛНИМОСТЬ не имеет решения в этом случае).

• Невозможно построить новую резольвенту (началось зацикливание). В этом случае делается вывод о выполнимости исходной системы дизъюнктов.

Проблема метода резолюций – его неэффективность в сложностном смысле. Найти эффективный алгоритм для задачи ВЫПОЛНИМОСТЬ или доказать, что такого алгоритма нет – одна из глобальных нерешенных задач современности. Различные модификации принципа резолюций направлены на сокращение перебора.