Глава 2. Модели множественной регрессии

2.1. Постановка задачи и основные понятия

При изучении изменения какого-либо фактора в большинстве случаев приходится рассматривать его во взаимосвязи не с одним, а с целым рядом влияющих на него факторов. Например, спрос на какой-либо товар зависит не только от цены на него, но и от уровня дохода потребителей, цены на сходные товары, национальных приоритетов населения и т.д. При этом взаимосвязь между переменными, как и прежде, носит отчасти случайный (стохастический) характер.

Модель, отражающую стохастическую взаимосвязь одной переменной с несколькими, влияющими на нее, можно представить в виде:

(2.1)

Такую модель называют множественной регрессией. Здесь y – зависимая (результирующая) переменная, x₁, x₂,…, x_m – независимые, объясняющие переменные, ε – случайная составляющая.

Наиболее употребительны две формы модели множественной регрессии (2.1):

,

.

Основной задачей регрессионного анализа является выявление регулярной составляющей , максимально соответствующей имеющемуся массиву статистических данных. Массив статистических данных представляет собой ряд статистических наблюдений переменных, присутствующих в модели, и которые можно записать в виде следующей таблицы:

№ наблюдений	y	x1	x2	…	xm
1	y1	x11	x21	…	xm1
2	y2	x12	x22	…	xm2
…	…	…	…	…	…
n	yn	x1n	x2n	…	xmn

Полученное уравнение

(2.2)

называется уравнением множественной регрессии переменной у по переменным x₁, x₂,…, x_m. Оно позволяет наилучшим в определенном смысле образом восстанавливать значения переменной у по известным значениям объясняющих переменных.

2.2. Множественный корреляционный анализ

Главная особенность построения и анализа множественной регрессии связана с тем, что результирующая переменная у испытывает воздействие не одной, а нескольких объясняющих переменных, которые, в свою очередь, определенным образом влияют друг на друга. Исследование проблемы взаимного воздействия рассматриваемых показателей происходит в рамках корреляционного анализа, обычно предваряющего или сопровождающего процесс построения модели множественной регрессии.

Если предположить, что переменные связаны между собой приближенно линейным образом, то общую картину тесноты таких взаимосвязей отчасти можно отразить в матрице коэффициентов парных корреляций (или кратко – в корреляционной матрице):

.

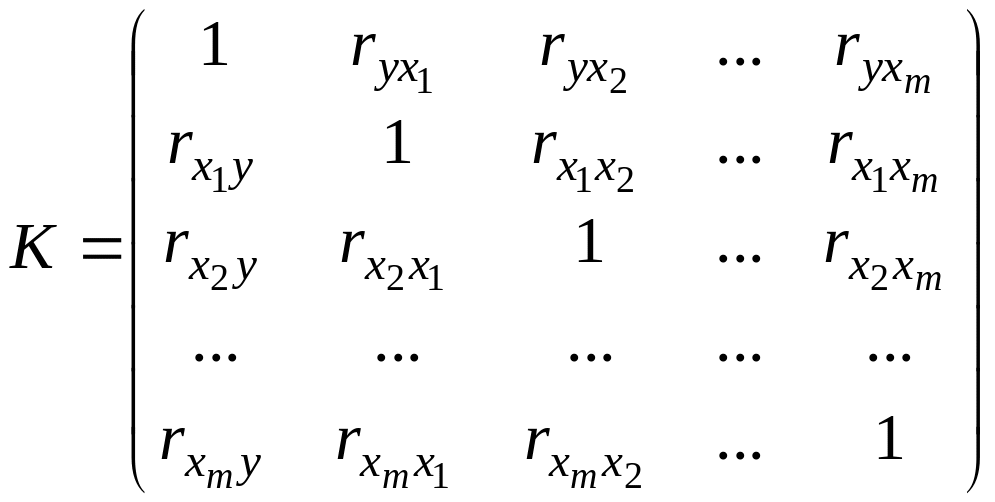В силу выполнения равенств и матрица K является симметричной.

По аналогии с линейными коэффициентами парных корреляций , совокупное влияние объясняющих переменных x₁, x₂,…, x_m на переменную у оценивается с помощью коэффициента множественной корреляции , который обозначается как , или просто R, если речь идет о фиксированном наборе объясняющих переменных (в [14] он обозначен как индекс множественной корреляции). Коэффициент множественной корреляции может быть рассчитан на основе корреляционной матрицы К по формуле:

,

где К₀ – матрица, полученная из матрицы К вычеркиванием первой строки и первого столбца; det(К) и det(К₀) - определители соответствующих матриц.

Отметим некоторые свойства коэффициента множественной корреляции:

а) значение коэффициента лежит в пределах от 0 до 1;

б) значение коэффициента должно быть больше или равно максимальному парному коэффициенту корреляции:

;

в) присоединение каждой новой объясняющей переменной не может уменьшить величины коэффициента множественной корреляции (независимо от порядка присоединения).

Специфическими показателями множественного корреляционного анализа являются так называемые частные коэффициенты корреляции, характеризующие степень взаимодействия пар переменных при неизменном уровне других переменных из рассматриваемого набора. Наиболее значимыми для исследования являются частные коэффициенты корреляции результирующего признака у с каждым из факторных признаков x₁, x₂,…, x_m , которые будем обозначать . Эти коэффициенты отражают действительное влияние каждого из факторов x_i на у, «очищенное» от влияния прочих факторов x₁, x₂,…x_i-1, x_i+1,...,x_m Частные коэффициенты корреляции могут быть рассчитаны по формуле:

, i=1,…,m (2.3)

где c₀₀, c_0i, c_ii - элементы матрицы

,

обратной к корреляционной матрице К: . Для удобства расчетов первая строка и первый столбец в этой матрице обозначены нулевыми индексами, индексы остальных строк и столбцов соответствуют индексам объясняющих переменных.

Если в исходной модели множественной регрессии присутствует всего два объясняющих признака х₁ и х₂ (случай двухфакторной регрессионной модели), то формула (2.3) может быть преобразована к частным формулам вида:

и .

Частные коэффициенты корреляции, как и общие коэффициенты, изменяются в пределах от 1 до 1. Так как частные коэффициенты корреляции дают меру тесноты связи каждого фактора с результатом в чистом виде, то сравнение их друг с другом позволяет ранжировать факторы по степени влияния их на результирующий показатель.

Проверка статистической значимости частного коэффициента корреляции проводится по той же схеме, что и для общего коэффициента корреляции, описанной в параграфе 1.3 первой главы. Отличие состоит лишь в изменении числа степеней свободы:

• по заданному значению коэффициента рассчитывается наблюдаемое значение соответствующей t-статистики:

;

• определяется табличное значение t_табл, представляющее собой критическую точку распределения Стьюдента для двусторонней критической области с заданным уровнем значимости  и числом степеней свободы k=nm1: t_табл=t(, nm1);

• сравниваются наблюдаемое и табличное значения: если , то соответствующий коэффициент корреляции статистически значим и взаимосвязь между переменными х_i и у существенная.

Частные коэффициенты корреляции могут быть использованы на этапе спецификации при отборе объясняющих переменных для потенциальной регрессионной модели. На первом шаге рассматривается полный набор факторов и на основе исходного массива данных по формулам (2.3) рассчитываются частные коэффициентов корреляции . На втором шаге отбирается фактор с наименьшей и несущественной по t-критерию Стьюдента величиной показателя частной корреляции. Исключив его из модели, рассчитываем новые частные коэффициенты корреляции относительно сокращенного набора переменных. Процедура продолжается до тех пор, пока не окажется, что все частные коэффициенты корреляции существенно отличаются от нуля, т.е. являются статистически значимыми.

Замечание 2.1. В случае, когда взаимосвязи между переменными являются нелинейными, множественный корреляционный анализ может быть проведен относительно некоторых функций переменных, входящих в модель, например, относительно их логарифмов.