Лемма 1

Каково бы ни было целое число n≥1, число различных размещений по одному объекту из заданных n равно:

У нас n объектов. Мы можем выбрать каждый объект только одним способом.

Число есть суммарное число различных способов, какими один объект может быть выбран из n объектов. Выбранным может быть либо первый, либо второй, либо третий …. либо n-ый:

Лемма 2

Каковы бы ни были n≥2, 1<k≤n, число различных размещений

Доказательство:

1,2,3,…k-1,k,…n

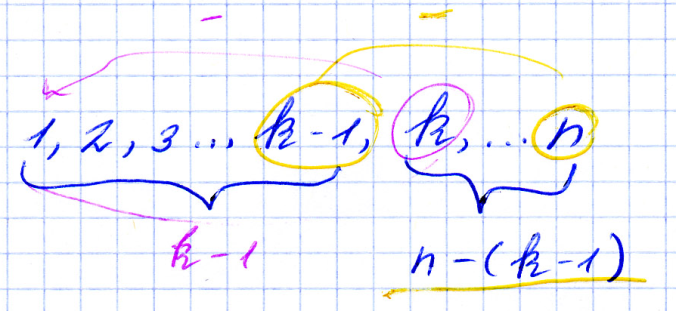
Пусть имеется размещение k-1 объектов из n объектов. В этом размещении имеется (k-1) упорядоченно размещенных объектов и (n-(k-1)) оставшихся неразмещенных объектов. На следующую k-тую позицию можно выбрать любой из оставшихся неупорядоченных объектов. Таким образом, каждому конкретному размещению (k-1) объектов из n можно поставить в соответствие (n-(k-1)) размещений k объектов из n. Это означает что A из n по k должно быть больше чем A из n по k-1 в (n-(k-1)) раз.

Теорема

Каковы бы ни были числа 1≤k≤n, число размещений

По второй лемме:

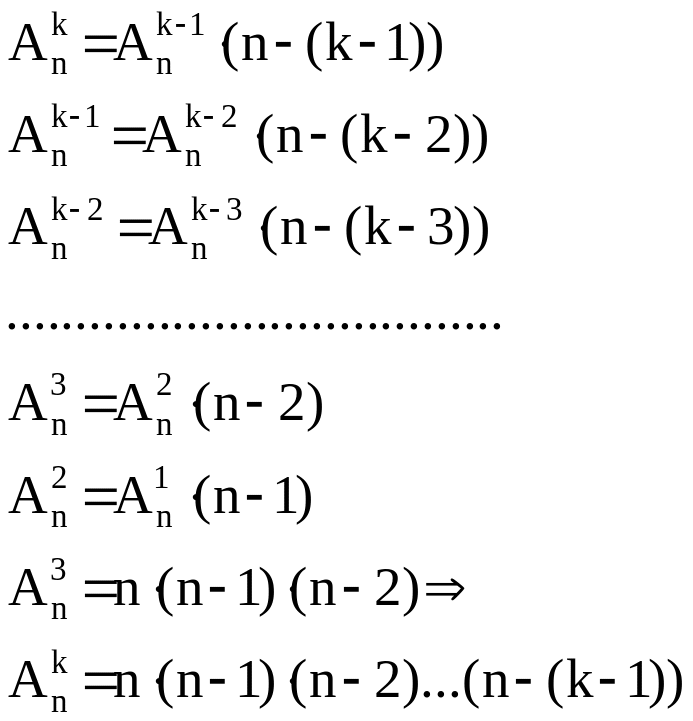
Определение

Событие называется случайным в данном опыте, если оно может произойти, а может и не произойти в этом опыте.

Все возможные в данном опыте исходы составляют множество Ω, которое называется пространством элементарных исходов или элементарных событий.

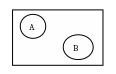
О. Событие – это произвольный набор элементарных исходов, или произвольное подмножество множества элементарных исходов Ω.

События обозначают латинскими буквами A, B, H… Для наглядности события изображают на диаграмме Венна. Геометрически она совершенно не верна, но удобна для демонстрации множеств.

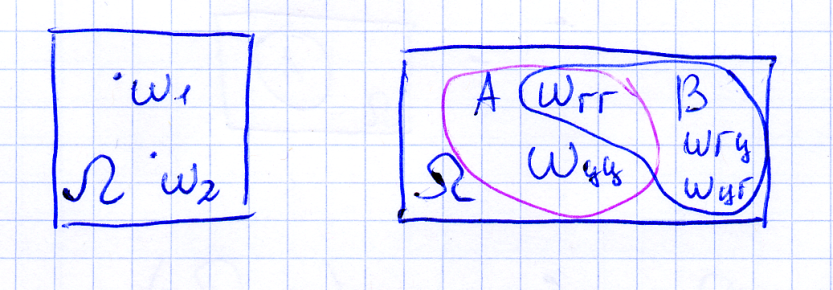
О. Событие, происходящее всегда ( при любом элементарном исходе ) называется достоверным и обозначается Ω.

О. Невозможное событие не происходит никогда (не содержит ни одного элементарного исхода). Обозначается как пустое множество .

Классическое определение вероятности

О. События считают равновозможными, если нет оснований полагать, что одно событие является более возможным, чем другие.

О. Вероятностью события A называется отношения числа k благоприятных для события A благоприятных исходов к общему числу равновозможных элементарных исходов n.

Всего 10 шаров, 4 синих, 6 красных. Вероятность вытащить синий:

Свойства вероятности:

1) Вероятность достоверного события равна единице:

2) Вероятность невозможного события равна нулю:

3) Вероятность случайного события заключена между нулем и единицей 0<P(A)<1

Вероятность любого события изменяется от нуля до единицы

Свойство 1. Сумма вероятности двух противоположных событий равна единице

Пример:

Найдите вероятность того, что при бросании двух игральных кубиков в семе выпадет не менее 4 очков.

A: ”Не менее 4х очков в сумме при бросании 2х кубиков”

ВОПРОС № 3

Теорема о вероятности суммы событий. Условная вероятность. Теорема о вероятности произведения событий. Зависимые и независимые события.

Теорема о вероятности суммы событий

Вероятность суммы двух событий равна сумме вероятности этих событий без вероятности их произведения:

P(A+B)=P(A)+P(B)-P(AB)

Доказательство:

Пусть имеется n всех элементарных исходов.

Количество исходов, благоприятных для события A: l+S

Количество исходов, благоприятных для события B: m+s

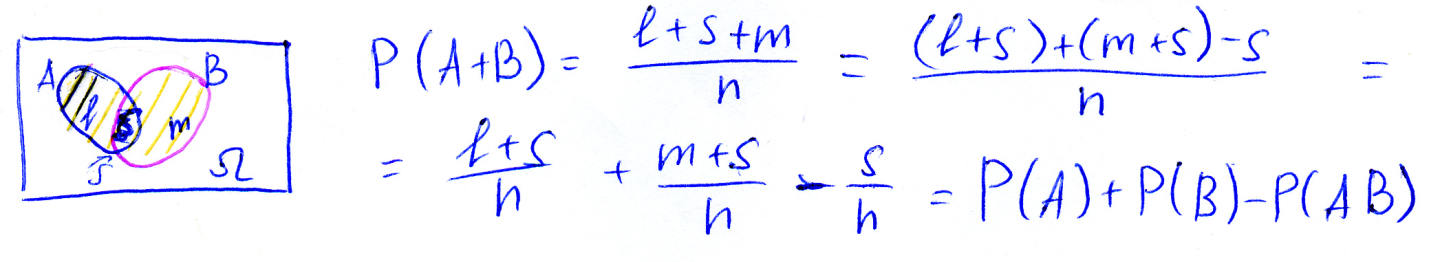Вероятность суммы двух несовместных событий равна сумме вероятности этих событий P(A+B)= P(A)+P(B)

Сумма вероятности трёх событий равна:

P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)

P((A+B)+C)

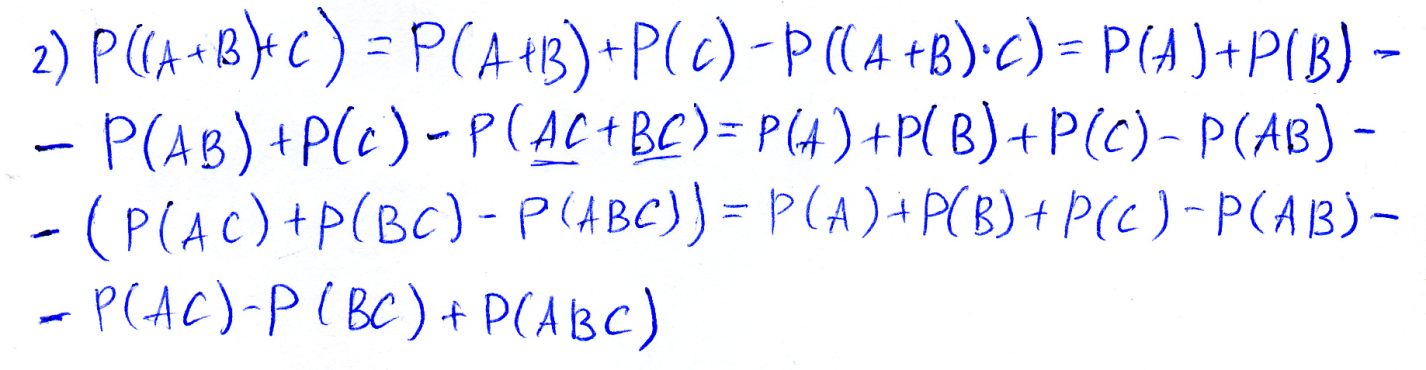Следствие 3

Вероятность суммы n событий равна P(A1+A2+…An)=P(A1)+P(A2)+…+P(An)-(P(A1A2)+P(A1A3)+ +P(A2A3)+…)+(-1)^n-1*P(A1A2A3…An)

Пример:

При бросании 2х кубиков найти сумму событий A и B.

A: сумма очков не более 4

B: выпадение одновременно одинакового числа очков на двух кубиках

K(A)=6; n=36

2 – 1вар

3 – 2вар

4 – 3вар

k (B)=6;

P(A+B)= P(A)+P(B)-P(AB)

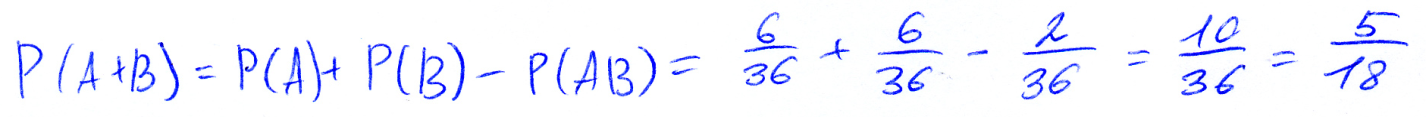k(AB)=2