Вопрос 37

Формула Тейлора для многочленов.

Пусть задана функция f(x) и в некоторой точке “а” нам известны значения её и её первых n производных: f(a), f ^I(a), f ^II(a), … , f⁽ⁿ⁾(a). Мы хотим построить такой многочлен T_n (х) степени n, который в некоторой окрестности точки «а» как можно меньше отличался бы от нашей функции. Для этого мы потребуем, чтобы в точке «а» значения многочлена и его производных совпадали, соответственно, со значениями функции и ее производных.

Итак, построим многочлен T_n (х), удовлетворяющих условиям:

T_n (а) = f(a), T_n^I(a) = f ^I(a), T_n^II(a) = f ^II(a), … , T_nⁿ(a) = f ⁿ(a).

Будем искать T_n(х) в виде

T_n(х)=c₀+c₁(x-a)+c₂(х-a)²+...+А_n(х-a)ⁿ

Ясно, что

T'_n(х)=c₁+2c₂(х-a)+3c₃(x-a)²+...+nc_n(x-a)^n-1,

T_n''(х)=2c₂+2•3c₃(х-a)+...+n(n-1)c_n(х-a)^n-2,

…………………………………………………..

T_n⁽ⁿ⁾(х) = n!c_n

Подставив в многочлен и его производные x=a, получим

с₀ = f(a), с₁ = f ^I(a), 2с₂ = f ^II(a), 3!с₃ = f ^III(a), … , n!с_n = f ⁽ⁿ⁾(a).

Отсюда

с₀ = f(a), с₁ = f ^I(a), ; , … ,

Таким образом

T_n (х) = f(a) + f ^I (a)(x-a) + *(x-a)² + ….. + *(x-a)ⁿ

Или, в более короткой записать,

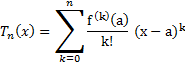Здесь, как это принято, считается, что f⁽⁰⁾ = f(a) и 0! = 1.

Формула Тейлора для функции

Рассмотрим подробнее величину R_n+1(x).

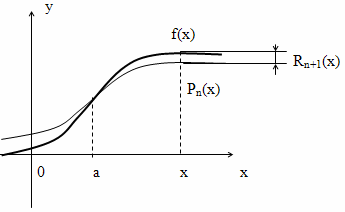
Как видно на рисунке в точке х = а значение многочлена в точности совпадает со значением функции. Однако, при удалении от точки х = а расхождение значений увеличивается.

Иногда используется другая запись для R_n+1(x). Т.к. точка ε ∈ (a,x), то найдется такое число θ из интервала 0 < θ < 1, что ε = a + θ(x - a).

Тогда можно записать:

Тогда, если принять a = x₀, x - a = Δx, x = x₀ + Δx, формулу Тейлора можно записать в виде:

где 0 < θ < 1

Если принять n=0, получим: f(x₀ + Δx) - f(x₀) = f'(x₀ + θΔx)Δx - это выражение называется формулой Лагранжа.

Формула Тейлора имеет огромное значение для различных математических преобразований. С ее помощью можно находить значения различных функций, интегрировать, решать дифференциальные уравнения и т.д.

Вопрос 38

Формула Тейлора для e^x и её применение в приближенных вычислениях.

Пусть f(x) = e^x. Тогда, как мы знаем, f^(k)(x) = e^x , а потому f^(k)(0) = 1, а f^(k)(с) = е^с.

Подставить всё это в или (0;x).

Получим формулу Тейлора для показательной функции:

Или в более подробной записи:

Отсюда следует приближённое равенство:

Позволяющее находить значение экспоненты.