Глава 2. Сбалансированные двоичные деревья
После каждой операции изменения дерева можно проводить балансировку дерева, которая позволяет минимизировать его высоту. При этом поиск по двоичному дереву будет требовать минимального времени. Балансировка позволяет также ускорить операции вставки и удаления узлов, которые тоже требуют проведения поиска.
К сожалению, пока нет способа проведения быстрой балансировки дерева до его минимальной высоты. Тем не менее, балансировка является очень эффективным методом. Мы не можем провести балансировку дерева до его минимальной высоты, но, задав критерий "разбалансированности" дерева перед проведением очередной балансировки, можно приблизиться к этой минимальной высоте. В этом случае, хотя мы и не получаем дерева с минимально возможной высотой в каждый момент времени, тем не менее, находимся близко к минимуму.
Алгоритм балансировки состоит из двух частей:
Дерево преобразуется в лозу.
Лоза перестраивается в сбалансированное дерево.
Лоза (vine) — это левоассоциативное двоичное дерево. Она имеет следующий вид:
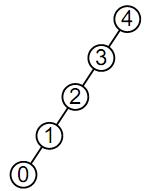
Рис.1. Левоассоциативное двоичное дерево – лоза
Главная лоза (рис.2) (main vine) — это левоассоциативное поддерево двоичного дерева.
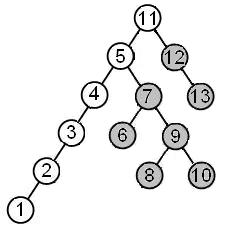
Рис.2. Левоассоциативное поддерево двоичного дерева
На рисунке вершины главной лозы окрашены в белый цвет.
2.1. Преобразование двоичного дерева в лозу.
Мы проходим по дереву указателем p, начиная в корне дерева. Вспомогательный указатель q указывает на родителя p (поскольку мы строим левоассоциативное дерево, то p всегда является левым ребенком q). На каждом шаге возникает одна из двух возможных ситуаций:
Если у p нет правого ребенка, то эта часть дерева уже перестроена. p и q просто спускаются по дереву (приравниваются своим левым сыновьям).
Если у p есть правый ребенок (обозначим его r), тогда выполняется левый поворот относительно p:
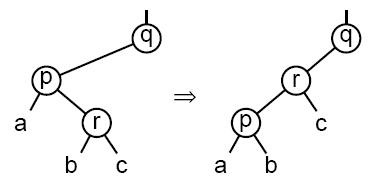
Рис. 3. Выполнение левого поворот
На рисунке a, b и c обозначают поддеревья, которые могут быть пусты. После поворота устанавливаем указатель p на r.
2.2. Преобразование лозы в сбалансированное двоичное дерево.
Этот этап алгоритма более содержательный и поэтому менее очевидный. Поэтому сначала будет разобран простой пример, а потом будет дано его обобщение.
Пусть есть лоза, которая состоит из 2n-1 вершин для какого-либо натурального n. Для примера возьмем n=4, тогда лоза будет содержать 15 вершин. Преобразуем данную лозу в сбалансированное дерево за три операции перестроения.
На первой операции пройдем по лозе сверху вниз, начиная в корне, и раскрасим каждую вершину соответственно в серый или черный цвет (условимся, что корень будет серого цвета). Затем возьмем каждую серую вершину, кроме самой нижней, сделаем ее правым ребенком черной вершины, являющейся ее левым ребенком. Т.е. выполним малый правый поворот относительно каждой серой вершины, кроме самой нижней (на рисунке 4 приведен пример малого правого поворота относительно вершины X).
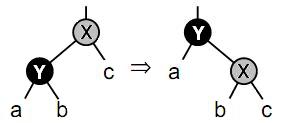
Рис.4. Малый правый поворот относительно вершины X
Таким образом, вместо лозы, состоящей из 15 вершин, мы получим дерево, состоящее из 7 черных вершин и 8 серых вершин (Рис.5).
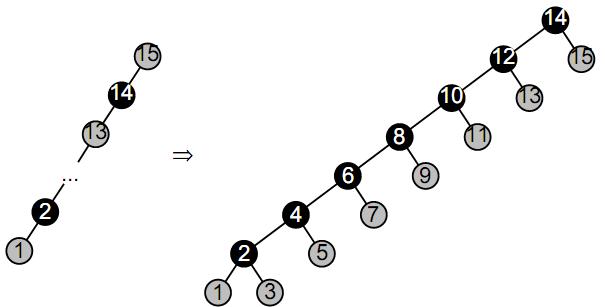
Рис.5. Первое перестроение
Для второго перестроения (рис.6) сначала перекрасим серые вершины в белые. Далее перекрасим каждую вторую черную вершину в серый цвет, начиная в корне. Теперь, как и раньше, выполним малый правый поворот относительно каждой серой вершины, кроме самой нижней.
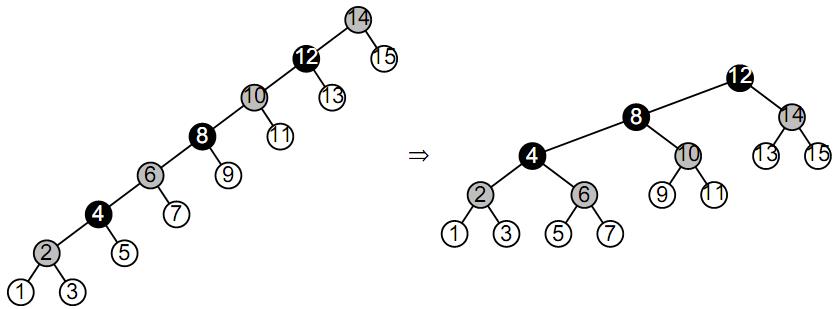
Рис.6. Второе перестроение
Третье перестроение аналогично первым двум. Вершины 12 и 4 перекрашиваются в серый цвет, затем выполняется малый правый поворот относительно вершины 12. В результате получается сбалансированное дерево.
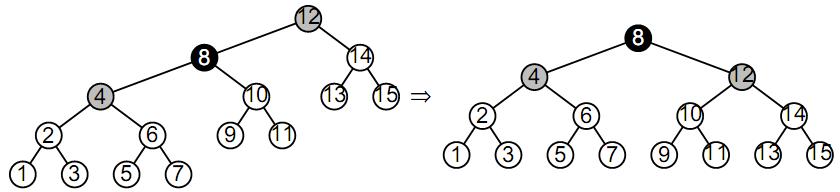
Рис.7. Третье перестроение
Теперь необходимо разобраться со случаем, когда длина лозы не может быть представлена в виде 2n-1 для какого-либо натурального n. В этом случае необходимо привести длину главной лозы к требуемому значению.
Пусть лоза состоит из m вершин. Тогда существует такое n, что (2n-1) < m < (2n+1-1). Необходимо укоротить главную лозу на m – (2n-1) вершин. После этого можно перестроить получившееся дерево аналогично способу, описанному выше. В результаты получится сбалансированное дерево с m – (2n-1) листьями.
Для примера разберем случай, когда лоза состоит из 9 вершин. Отсюда следует, что n=3, т.к. (23-1)=7<9<15=(24-1). Следовательно, необходимо укоротить главную лозу на 9-(23-1)=2. После этого перестраиваем дерево аналогично примеру, приведенному выше. В результате у нас должно получиться сбалансированное дерево.
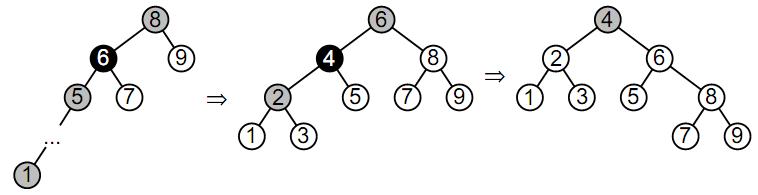
Рис.8. Сбалансированное дерево с m - (2n-1) листьями