Контрольные вопросы

1. Что означает термин «сбалансированное» дерево?

2. Для чего выполняется балансировка?

3. Опишите фазы балансировки.

4. Как происходит преобразование исходного дерева в лозу?

5. Как происходит преобразование лозы в сбалансированное дерево?

6. В каких случаях необходимо укорачивать лозу?

7. Как определить размер укорачивания?

8. Как происходит поворот относительно вершины?

9. Сколько вершин будет в сбалансированном дереве, если в исходном их 200?

Задания для практической работы

Требуется:

• запрограммировать алгоритм балансировки дерева;

• количество вершин лозы определяется случайно в диапазоне от 7 до 31;

• каждое перестроение выводить на экран.

Глава 3. Жадные алгоритмы

3.1. Понятие жадного алгоритма

Жадный алгоритм (англ. Greedy algorithm) — алгоритм, заключающийся в принятии локально оптимальных решений на каждом этапе, допуская что конечное решение также окажется оптимальным.

Общего критерия оценки применимости жадного алгоритма для решения конкретной задачи не существует, однако, для задач, решаемых жадными алгоритмами характерны две особенности:

во-первых, к ним применим Принцип жадного выбора ;

во-вторых, они обладают свойством Оптимальности для подзадач.

Говорят, что к оптимизационной задаче применим принцип жадного выбора, если последовательность локально оптимальных выборов даёт глобально оптимальное решение. В типичном случае доказательство оптимальности следует такой схеме: Сначала доказывается, что жадный выбор на первом шаге не закрывает пути к оптимальному решению: для всякого решения есть другое, согласованное с жадный выбором и не худшее первого. Затем показывается, что подзадача, возникающая после жадного выбора на первом шаге, аналогична исходной, и рассуждение завершается по индукции.

Говорят, что задача обладает свойством оптимальности для подзадач, если оптимальное решение задачи содержит в себе оптимальные решения для всех её подзадач. Например, в задаче о выборе заявок можно заметить, что если A — оптимальный набор заявок, содержащий заявку номер 1, то — оптимальный набор заявок для меньшего множества заявок , состоящего из тех заявок, для которых .

Пример 1: Размен монет.

Условие: Монетная система некоторого государства состоит из монет достоинством a₁ = 1 < a₂ < ... < a_n. Требуется выдать сумму S наименьшим возможным количеством монет.

Жадный алгоритм решения этой задачи таков. Берётся наибольшее возможное количество монет достоинства a_n: . Таким же образом получаем, сколько нужно монет меньшего номинала, и т. д.

Для данной задачи жадный алгоритм не всегда даёт оптимальное решение. Например, сумму в 10 копеек монетами в 1, 5 и 6 коп. жадный алгоритм разменивает так: 6 коп. — 1 шт., 1 коп. — 4 шт., в то время как правильное решение — 2 монеты по 5 копеек. Тем не менее, на всех реальных монетных системах жадный алгоритм даёт правильный ответ.

3.2. Алгоритм Хаффмана

Алгоритм Хаффмана (англ. Huffman) — адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году доктором Массачусетского технологического института Дэвидом Хаффманом. Коды Хаффмана широко используются при сжатия информации (в типичной ситуации выигрыш может составить от 20% до 90% в зависимости от тина файла). Алгоритм Хаффмана находит оптимальные префиксы (коды символов), исходя из частоты использования этих символов в сжимаемом тексте, с помощью жадного выбора.

Пусть в файле длины 100 000 известны частоты символов.

Мы хотим построить двоичный код, в котором каждый символ представляется в виде конечной последовательности битов, называемой кодовым словом.

Таблица 1.

Коды символов

	а	b	с	d	е	f
Количество (в тысячах)	45	13	12	16	9	5
Равномерный код	000	001	010	011	100	101
Неравномерный код	0	101	100	111	1101	1100

При использовании равномерного кода, в котором все кодовые слова имеют одинаковую длину, на каждый символ (из шести имеющихся) надо потратить как минимум три бита, например, а — 000, b — 001,.. .,f — 101 (таб.1.). На весь файл уйдет 300 000 битов .

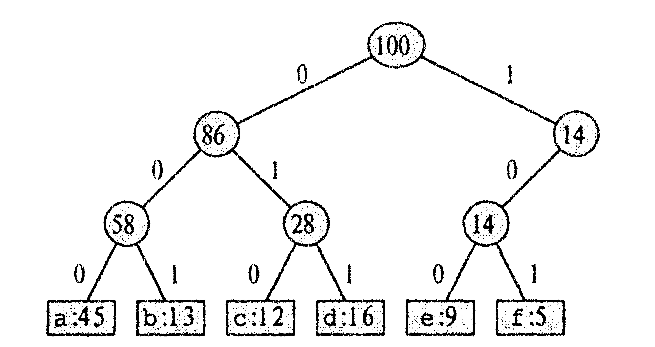
Рис.1. Представление равномерного кода в виде дерева

Неравномерный код будет экономнее, если часто встречающиеся символы закодировать короткими последовательностями битов, а редко встречающиеся длинными.

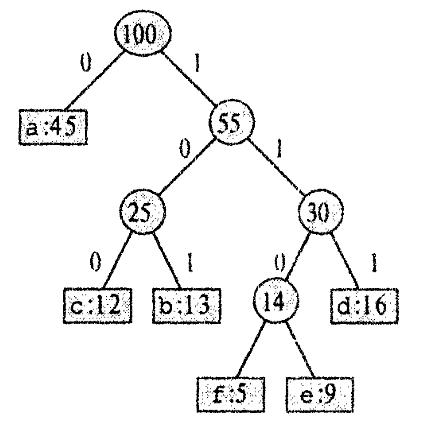
Рис.2. Представление неравномерного кода в виде дерева

. Один такой код показан на рис.2: буква а изображается однобитовой последовательностью 0, а буква f четырёхбитовой последовательностью 1 100. При такой кодировке на весь файл уйдёт (45- 1 + 13-3+ 12-3+ 16-3 + 9-1 +5-1) * 1000 = 221000 битов, что даёт около 25% экономии.

Этот метод кодирования состоит из двух основных этапов:

1. Построение оптимального кодового дерева.

2. Построение отображения код-символ на основе построенного дерева.

Общая схема построения дерева Хаффмана (рис.3):

1. Составим список кодируемых символов (при этом будем рассматривать каждый символ как одноэлементное бинарное дерево, вес которого равен весу символа).

2. Из списка выберем 2 узла с наименьшим весом (под весом можно понимать частоту использования символа — чем чаще используется, тем больше весит).

3. Сформируем новый узел и присоединим к нему, в качестве дочерних, два узла выбранных из списка. При этом вес сформированного узла положим равным сумме весов дочерних узлов.

4. Добавим сформированный узел к списку.

5. Если в списке больше одного узла, то повторить 2-5.

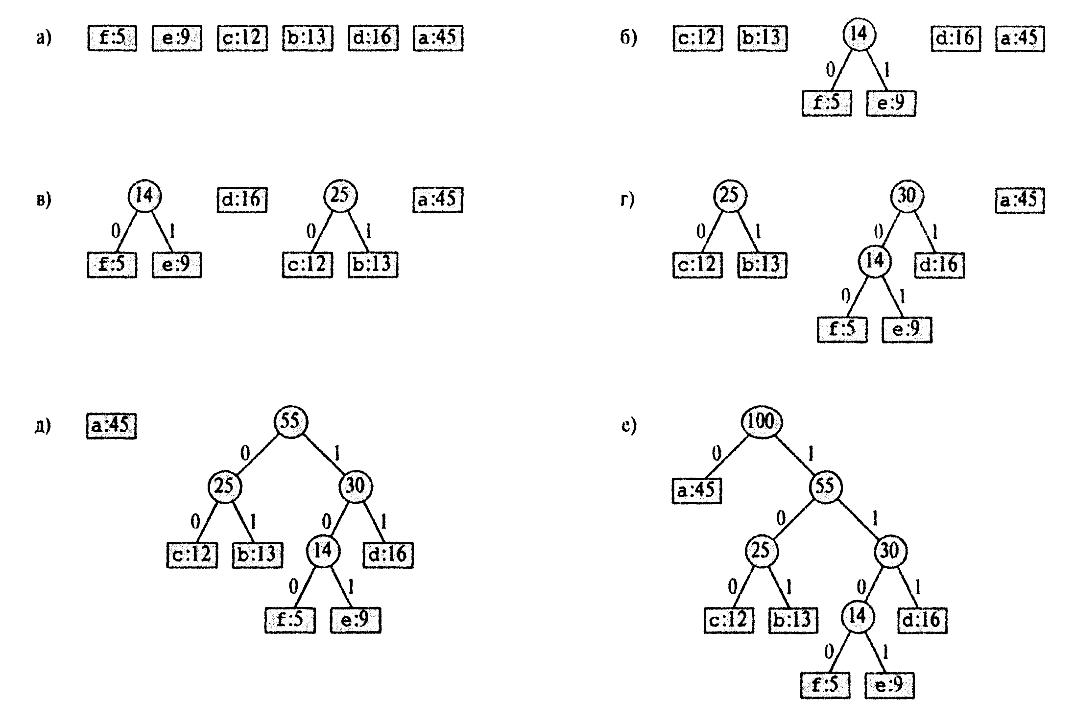
Рис.3. Этапы построения дерева Хаффмана