1. Числовые ряды.

Пусть дана числовая последовательность . выражение вида

(1) называют числовым рядом (рядом).

Числа называют членами ряда, число a_n с общим номером n называют общим членом ряда.

2. Последовательность частичных сумм. Сумма ряда. Сходящиеся ряды.

Сумма конечного числа первых членов ряда:

называют частными суммами ряда (1). Т.к. число членов ряда бесконечно, то частичные суммы образуют последовательность (2)

Ряд (1) называют сходящимся, если последовательность (2) его частичных сумм сходится к некоторому числу S . в этом случае число S называют суммой ряда (1). В противном случае ряд- расходящийся.

В случае сходимости записывается

3. Свойства сходящихся рядов

1. Если ряд сходится, то сходится любой из его остатков. Наоборот, из сходимости какого-то остатка вытекает сходимость всего ряда. Отсюда следует, что изменение или выбрасывание конечного числа членов ряда не изменяет его сходимости или расходимости.

2. Если ряд сходится, то .

3. Если ряд сходится, то сходится ряд и имеет место равенство =c

4. Если ряды и сходятся, то сходится и ряд имеет место равенство = +

4. Необходимое условие сходимости числового ряда.

Если ряд сходится, то предел его общего члена равен 0.

( если предел общего члена не равен нулю или не существует, то данный ряд расходится)

Доказательство:

Пусть данный ряд сходится и его сумма равна S. Для любого натурального n имеем или (3)

При обе частичные суммы стремятся к пределу S, поэтому из равенства (3) следует, что

.

5. Числовые ряды с неотрицательными членами.

Ряд вида а₁+а₂+…+а_n+…, все члены которых положительны.

6. Критерий сходимости числовых рядов с неотрицательными членами.

Критерий сходимости

Для того чтобы ряд с положительными членами сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.

Доказательство

Необходимость. Пусть ряд сходится. Тогда существует предел его частичных сумм. Из свойств пределов следует, что последовательность частичных сумм ограничена.

Достаточность. Поскольку все члены данного ряда положительны и для любого n , то последовательность его частичных сумм монотонно возрастает. Однако известно, что ограниченная сверху последовательность имеет предел.

7. Признаки сравнения, признак Даламбера и Коши, интегральный признак для числовых рядов с неотрицательными членами.

Первый признак сравнения.

Пусть даны два ряда с положительными членами:

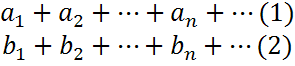
Причем члены первого ряда не превосходят соответствующие члены второго ряда: . Тогда из сходимости ряда (2) («большего») следует сходимость ряда (1) («меньшего»). Эквивалентно- из расходимости меньшего следует расходимость большего.

Второй признак сравнения

Если для рядов (1) и (2) с положительными членами существует отличный от нуля предел отношения

, (4)

то ряды (1) и (2) сходятся или расходятся одновременно.

Признак Даламбера

Если для ряда с поло­жительными членами a₁ + а₂+... + а_n +... существует такое чис­ло q < 1, что при всех n (или начиная с некоторого n) выпол­няется неравенство

(6)

то ряд сходится. Если же > 1 для всех или начиная с некоторого n, то ряд расходится

8. Знакопеременные ряды. Абсолютная и условная сходимость.

Особенно часто среди знакопеременных рядов встречаются ряды, члены которых имеют чередующиеся знаки, т.е. знакоче­редующиеся ряды.

Условимся считать первый член ряда положительным; тогда знакочередующийся ряд в общем виде запишется так:

(1)

где все а_п положительны (n = 1,2, ...).

u₁ + u₂ + u₃ + . . . + u_n + . . .(1)-знакопеременный ряд

|u₁| + |u₂| + |u₃| + . . . + |u_n| + . . . (2) –знакопеременный ряд, составленный из абсолютных величин его членов.

(*)

Ряд 1 называют абсолютно сходящимся, если сходится ряд 2, составленный из модулей его членов. Справедливо и обратное утверждение.

Ряд 1 называют условно сходящимся, если ряд 1 сходится, а ряд 2 расходится.

9. Признак лейбница для знакочередующихся числовых рядов.

(теорема Лейбница). Если члены знакочереду­ющегося ряда убывают по абсолютной величине и стремят­ся к нулю, когда п →∞, то 1) ряд сходится; 2) любой остаток ряда не превосходит по абсолютной величине первого из сво­их членов и имеет одинаковый с ним знак.

10. Степенные ряды.

Ряд вида a₀+a₁x+a₂x²+…+a_nxⁿ+… (1)

Где a_0, а₁, а₂,…,а_n,…-некоторая числовая последовательность, называют степенным рядом.

a_0, а₁, а₂,…,а_n- коэффициенты степенного ряда

11. Теорема Абеля

1. Если степенной ряд 1 сходится при некотором х=х₀, не равном нулю, то он сходится, и притом абсолютно, при всех х, удовлетворяющих условию |x|<|x₀|;

2. Если ряд 1 расходится при некотором х=х₁, то он расходится при всех х, удовлетворяющих условию |x|>|x₁|

12. Интервал и радиус сходимости степенного ряда

Множество U с R называется областью сходимости функционального ряда , если для каждого значения x₀ϵU сходится числовой ряд , а для x не принадлежащем U числовой ряд расходится.

, где R-радиус сходимости

(x₀-R, x₀+R)-интервал сходимости. На всем этом интервале ряд сходится.

13. Интегрируемость и дифференцируемость суммы степенного ряда на интервале сходимости.

Теорема о почленном диф-ии степенного ряда. Пусть ф-я f(x) разлагается на интервале (-R;R) в степенной ряд a₀+a₁x+a₂x²+…+a_nxⁿ+(1)…. Рассмотрим степенной ряд a₁+2a₂x+a₃x²+…+a_nx^n-1+…(2), полученный почленным дифференцированием ряда 1. Тогда

1. Ряд 2 имеет тот же радиус сходимости R, что и ряд 1

2. На всём интервале (-R;R) ф-я f(x) имеет производную f’(x), которая разлагается в степенной ряд 2

Теорема о почленном интегрировании степенного ряда. Если ф-я f(x) разлагается на интервале (-R;R) в степенной ряд, то она интегрируема на этом интервале, интеграл от суммы ряда равен сумме интегралов от членов ряда.

14. Ряды Тейлора (Маклорена)

Если ф-я бесконечно диф-ма на некотором интервале (x0 − R, x0 + R) и имеет ограниченные производные |f⁽ⁿ⁾(x)| < MϵR, для всех x ϵ (x0 − R, x0 + R) и n ϵ N, то на этом интервале справедливо равенство:

Если х₀=0, то ряд Тейлора можно записать в виде:

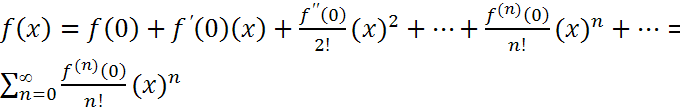
Он называется рядом Маклорена.

15. Достаточное условие разложимости в ряд Маклорена

Пусть ф-я f(x) определена и бесконечно диф-ма на интервале (-r;r). Если сущ-т такая константа М, что во всех точках интервала вып-ся нер-ва

, то в этом интервале ряд Маклорена сходится к ф-ии f(x)/

16. Разложение в ряд Маклорена функций e^x, sin x, cos x, 1/(1+x), ln(1+x), (1+x)^a

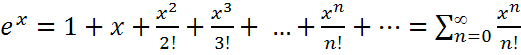
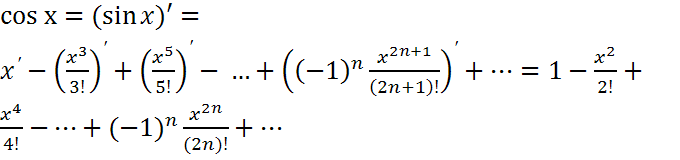
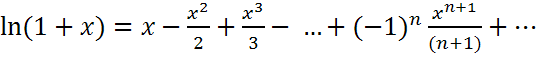
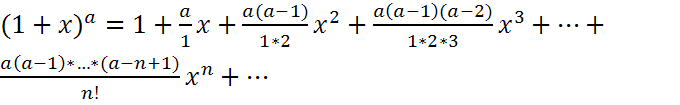
17. Пространство Rⁿ.

n-мерное векторное пространство вводится на основе сопоставления с множеством векторов на плоскости и в пространстве.

Rⁿ=R*R*R…R-арифметическое пространство элементами которого являются точки х_i ϵ R(i=1…n)

18. Расстояния в Rⁿ. Свойства расстояния.

Пусть х=(х₁, х₂, …), у=(у₁, у₂….), тогда ρ(х,у)= называется расстоянием между точками х и у в Rⁿ

Св-ва расстояния

1. ρ(х,у)≥0

2. ρ(х,у)= ρ(у,х)

3. ρ(х,у)+ ρ(у,z)≥ ρ(х,z)

19. Окрестность точки в Rⁿ

δ-окрестностью точки хϵ Rⁿ множество точек у из Rⁿ, такие, что ρ(х,у)≤δ

обозначение U_δ(x)

20. Внутренние и граничные точки множества

Точка х называется граничной точкой множества Х, если для любого δ>0:

U_δ(x)

U_δ(x) , где СХ - дополнение множества Х до Rⁿ(СХ= Rⁿ\Х)

21. Открытые и замкнутые множества

Мн-во называется открытым, если все его точки внутренние.

Если мн-во содержит все свои граничные точки, то оно замкнутое.

22. Изолированные и предельные точки множества

Точка х₀ϵХ называется изолированной для Х, если существует U_δ(x): для любого х≠ х_0, хϵ U_δ(х₀), хϵХ

23. Ограниченные множества

Мн-во Х называется ограниченным, если сущ-т c>0, СϵR: для любого х=(х₁, х₂,…)ϵХ |x_i|<C( i=1…n)

24. Сходимость последовательности точек Rⁿ , ее сходимость покоординатной сходимости

Определение. Пусть {р_п} - последовательность то­чек в Rⁿ_. Мы говорим, что эта последовательность сходится к точке р₀, если числовая последовательность {р(р„, р₀)} имеет предел 0.

Иначе говоря, последовательность {р_n} сходится к р₀, если расстояние {ρ(р_n,р₀)} неограниченно уменьшается с ростом n.

Можно дать и другое определение сходящейся последователь­ности - не через расстояние между точками, а через координаты точек. Для сокращения записей дадим это определение для п = 2.

Определение. Пусть р₁ = (х₁, у₂) р₂ = (х₂, у₂),... - пос­ледовательность точек в R². Мы скажем, что эта последо­вательность сходится к точке р₀ = (x₀, у₀), если числовая последовательность х₁, х₂, ... сходится к числу x₀, а числовая последовательность у₁, у₂, ... - к числу у₀.

Дайте определение числового ряда и его суммы. Найдите, исходя из

определения, сумму ряда Σ∞ qn при q <1.