MatAn_practice

Министерство образования и науки Российской Федерации Уральский федеральный университет

имени первого Президента России Б.Н. Ельцина

Н. В. Чуксина, Р. М. Минькова

Руководство к решению задач по математическому анализу

Учебное пособие для студентов физико-технологического института

Екатеринбург

УрФУ

2013

УДК 517(075.8) ББК 22.161я73

Рецензенты:

кафедра прикладной математики Уральского государственного экономического университета (зав. кафедрой, доц., канд. физ.-мат. наук Ю.Б. Мельников);

старший научный сотрудник Института математики и механики УрО РАН,

проф., д-р физ.-мат. наук Е.Ф. Леликова;

Научный редактор − доц., канд. физ.-мат. наук Е.А. Голикова

Авторы: Н.В. Чуксина, Р.М. Минькова, В.В. Трещева

Ч 79 Руководство к решению задач по математическому анализу.

Учебное пособие для студентов физико-технологического института. / Н.В. Чуксина, Р.М. Минькова, В.В. Трещева. Екатеринбург:УРФУ, 2013. 56 с.

ISBN 5-321-00550-8

В учебном пособии разбирается решение типовых примеров и задач по следующим темам: предел, непрерывность, дифференцируемость функции одной переменной, общие теоремы анализа, исследование функций и построение их графиков, неопределенный определенный, несобственный интегралы. Пособие предназначено для студентов технологических специальностей физикотехнического факультета.

Библиогр.: 9 назв. Рис. 20

Подготовлено кафедрой «Вычислительные методы и уравнения математической физики» при поддержке физико-технического факультета

УДК 517.2/.3 (075.8) ББК 22.161.1я73

ISBN	© Уральский федеральный университет, 2013

2

Оглавление

1.Предел функции и последовательности………………………………….…......4

1.1.Определение предела функции и последовательности…….…………......4

1.2.Предел элементарной функции………….………………………..………....6

	1.3. Бесконечно малые функции. Неопределенность		0		……………….….....6
			0
	1.4. Бесконечно большие функции. Неопределенности						, , 0 ….9

1.5.Второй замечательный предел. Неопределенность 1 …………..…….10

2.Непрерывность функции………………………………………………………..12

3.Производные……………………………………………………………………..14

3.1.Определение производной идифференциала..……..…………………….14

3.2.Геометрический смысл производной……………..………………………15

3.3.Дифференцирование по формулам…………………..….………………...16

3.4.Логарифмическое дифференцирование………………..…………………17

3.5.Дифференцирование параметрически заданных функций.……………..18

3.6.Правило Лопиталя………………………………………………..………..19

3.7.Формула Тейлора……………………………………………………..……21

4.Исследование функций. Построение графиков……………………………….22

5.Неопределенный интеграл………………………………………………………27

5.1.Таблица основных интегралов……………………………………………27

5.2.Метод подведения под знак дифференциала…………………………...28

5.3.Метод интегрирования по частям……………………………………….29

5.4.Метод замены переменной……………………………..…………………1

5.5.Интегрирование тригонометрических функций ……..…………………3

5.6.Интегрирование функций, содержащих квадратный трехчлен………..36

5.7.Интегрирование рациональных дробей…………………………………37

6.Определенный интеграл.......................................................................................39

6.1.Свойства определенного интеграла ..........…….....................................40

6.2.Методы вычисления определенного интеграла…..……….….….……42 6.3 Геометрические приложения определенного интеграла…..…..…..….46

7.Несобственные интегралы………..………..………………………..……..…..50

7.1.Несобственные интегралы первого рода …….........………..….……50

7.2.Несобственные интегралы второго рода ……...……..……..….……52

Библиографический список………………………………………………………..55

3

1.Предел функции и последовательности

1.1.Определение предела функции и последовательности

Пример 1.1. Записать определение предела функции на языке окрестностей и на языке неравенств:

а) lim f (x) 2;		б) lim f (x) 0;	в) lim f (x) .
x 1		x	x 3
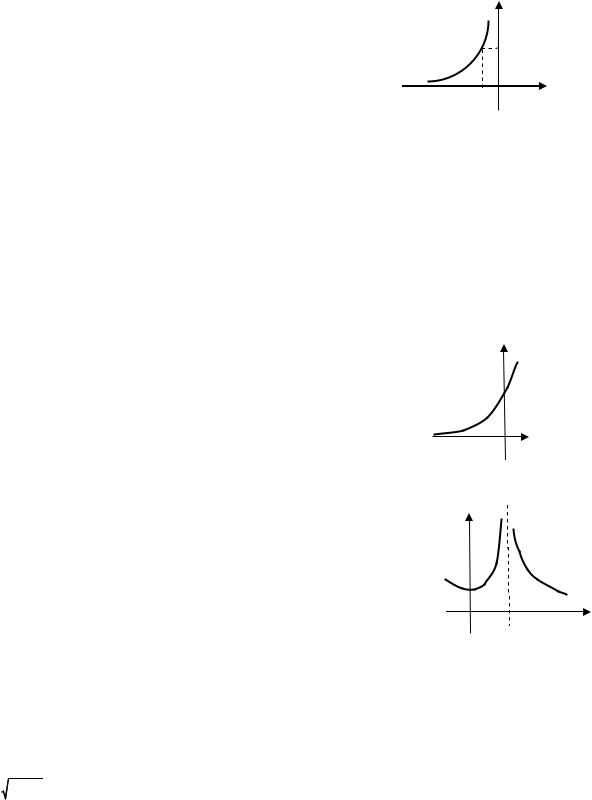
Решение. а).		lim f (x) 2, если для всех x, достаточно		y
	x 1
близких к −1, соответствующие значения			f x как	2
угодно близки к 2 (рис.1).
Поясним: f (x)		как угодно близко к 2, то есть		1	x
		f (x) S (2) для 0;
				Рис.1
			o
x достаточно близко к −1, то есть 0: x S ( 1)).
Определение на языке окрестностей:
lim f (x) 2, если для любого числа 0			существует такое число ( ) 0,
x 1
что значения		f (x) будут принадлежать -окрестности точки 2 для всех x, при-
надлежащих выколотой -окрестности точки −1. Или кратко:
для 0	( ) 0 такое, что f (x) S (2)		o
			для всех x S ( 1).
Определение на языке неравенств: lim f (x) 2, если для 0				( ) 0 такое,
		x 1

что | f (x) 2|	как только 0 | x 1| .
б). lim f x 0	(рис.2).
x
На языке окрестностей.
lim f (x) 0,если для 0		( ) 0такое, что
x
	f (x) S (0) для x S ( ).
На языке неравенств:
lim f (x) 0, если для 0 ( ) 0 такое, что
x
	| f (x)| для x .
в). lim f (x) (рис.3).
x 3
На языке окрестностей:
lim f (x) , если для 0		( ) 0 такое, что
x 3

y

x

0

Рис.2

y

x

3

						o	Рис.3
			f (x) S ( ) для x S (3).
	На языке неравенств: lim			f (x) , если для 0			( ) 0 такое, что
			x 3
			f (x) как только 0 | x 3| .
Пример 1.2. Доказать, пользуясь определением предела, что
	а) lim		3,	б) lim	sinn	0.
		x 4
	x 5			n n

4

Решение. а). По определению предела для 0 требуется найти соответству-

ющее ему

( ) 0

так, чтобы выполнялось неравенство

|

x 4 3| , как

только

0 | x 5| . Преобразуем выражение

|

3| :

x 4

3

3

x 4

x 4

x 5

.

x 4 3

x 4 3

x 4 3

Оценим это выражение сверху, учитывая, что

3 3. Тогда

x 4

1

1

1

и

3

x 5

x 5

,

x 4

x 4 3

x 4 3 3

x 4 3

3

как только

x 5

3 . Тогда в качестве искомого

можно взять 3 . Таким

образом, для любого 0

нашлось 3 такое,

что

3

, как только

x 4

для x выполнится условие 0 | x 5| 3 .

б). Для доказательства того, что

lim

sinn

0,

требуется для

n n

sinn

0

найти N 0 такое, что

для n N .

n

Так как

sin n

1, то

sinn

1

, как только n

1

. Таким образом, для любо-

n

n

sin n

го 0

нашли N

1

такое,

что

для n

1

.

n

Пример 1.3. Используя односторонние пределы функции, установить, суще-

1

x 2

ствует ли предел: а) lim 2

,

б) limarctg

.

x

x 0

x 1

x 1

Решение а). При x 0

1

1

имеем:

и

lim 2

x

;

x

x +0

при x 0

1

1

имеем:

и

lim 2

x

0.

1

1

x

x 0

1

Так как

lim 2

x

lim 2

x

, то lim 2

не существует.

x

x +0

x 0

x 0

б). Для функции arctg

x 2

x 1

при x 1 0 имеем:

x 2

x 2

x 2 3,

x 1 0,

и

lim

arctg

;

при x 1 0 имеем:

x 1

x 1 0

x 1 2

x 2

x 2

x 2 3,

x 1 0,

и

lim

arctg

.

x 1

x 1

x 1 0

2

Так как

lim arctg

x 2

lim arctg

x 2

, то

lim arctg

x 2

не существует.

x 1 0

x 1

x 1 0

x 1

x 1

x 1

5

Пример 1.4. Исследовать на сходимость последовательности

		2n	( 2)n				n
а)	un			, б) un ctg				.
			2n		4		2

Решение. а). Рассмотрим подпоследовательности u2k ,

u2k 1 и найдем их

пределы при k :

lim u2k lim

22k ( 2)2k

lim

2 22k

lim 2 2,

k

k

22k

k 22k

k

lim u2k 1

lim

22k 1 ( 2)2k 1

lim

0

0.

22k 1

k

k

k 22k 1

Так как пределы подпоследовательностей различны, то предела последовательности un не существует.

б). Рассмотрим подпоследовательности :

							2k
	u2k ctg
			4			2
u2k 1			(2k 1)
	ctg
		4				2

	ctg			k			ctg			1,
			4						4
											3
	ctg					k		ctg				1.
			4
				2					4

Найдем их пределы при k : lim u	2k lim1 1,	lim u	2k 1	lim( 1) 1.
k	k	k		k

Так как пределы подпоследовательностей различны, то предела последовательности не существует.

1.2. Предел элементарной функции

Предел элементарной функции при x a равен значению функции в точке a, если функция определена в этой точке.

Пример 1.5. Вычислить пределы: а) lim

5x2 2

; б) limsin

2x 1

.

x 0

2x 1

x 1

x

Решение.

а). Так как функция

f (x)

5x2 2

элементарна и определена при x 0, то

2x 1

0 2

lim f (x) f (0)

2 .

0 1

x 0

б). Так как функция

f (x) sin

2x 1

элементарна и определена при

x 1, то

x

lim f (x) f (1) sin 2 1 sin1.

x 1 1

1.3.Бесконечно малые функции. Неопределенность 0

0

Функция f (x)называется бесконечно малой при x a, если

lim f (x) 0 .

x a

Пример 1.6. Вычислить lim

f (x), где

x a

cos2 x

а) f (x) 4cosx sin

1

ln(1 x) ,

a 0 , б) f (x)

, a 1.

2 (e

x

x 1 1) arctg x 2 / x 1

6

Решение. а). Функция

f (x)

не определена в точке x 0.

Кроме того,

lim sin

1

не существует,

но

sin

1

1, то есть функция

sin

1

огра-

x 0

x

x

x

ничена.

Функция

ln(1 x)

есть

бесконечно

малая

при

x 0, так

как

lim ln(1 x) ln1 0.

По теореме о произведении бесконечно малой функции на

x 0

ограниченную функцию получаем, что sin

1

ln(1 x)

бесконечно малая функ-

ция

при

и

ее

предел

при

x

равен

нулю. Кроме

того,

x 0

x 0

lim 4cosx 4cos0 4. Поэтому

x 0

lim f (x) lim

4cosx sin

1

ln(1 x)

2.

4 0

x

x 0

x 0

б). Функция

f (x) не определена в точке x 1. Кроме того,

limarctg

x 2

не су-

x 1

x 1

ществует, но

arctg

x 2

,

значит,

функция arctg

x 2

ограничена.

x 1

2

x 1

x 1

Так как

lim

e

x 1 1 e

1 1 1 1 1 0

, то функция (e

x 1 1)

бесконечно малая

при

x 1.

Тогда по теореме о произведении бесконечно малой функции на

ограниченную получаем,

что

(e

1) arctg

x 2

бесконечно малая функция

x 1

x 2

x 1

при x 1

и

e

1

arctg

0.

Учитывая,

что limcos2 x cos2 1, по-

lim

x 1

x 1

лучим:

x 1

x 1

cos2 x

1

1

lim

.

x 2

x 1 2 (e

1)arctg

2 0

2

x 1

x 1

Пример 1.7. Вычислить пределы:

x3 x2 5x 3

3

3

а)

б)

x 4

2

;

в)

1 x

1 x

.

lim

;

lim

lim

x

x 1

3x2 2x 5

x 0 x 9 3

x 0

Решение. а). Числитель P(x) x3 x2

5x 3

и знаменатель Q(x) 3x2

2x 5

дро-

би при

x 1 обращаются в ноль.

Значит,

имеем неопределенность вида

0

.

P x

и Q x ,

0

Так как

x 1 корень многочленов

то эти многочлены делятся

нацело на

x 1 . Поделив эти многочлены на

x 1 , можно разложить их на

множители:

x3 x2 5x 3 (x 1) (x2 2x 3),

3x2 2x 5 (x 1) (3x 5).

Значит,

lim

x3 x2

5x 3

lim

(x 1) (x2 2x 3)

lim

x2

2x 3

0.

(x 1) (3x 5)

x 1

3x2 2x 5

x 1

x 1

3x 5

б). При x 0 числитель и знаменатель дроби равны 0, следовательно, имеем

0

неопределенность . Так как и числитель, и знаменатель функции

0

7

g(x)

	f (x)		x 4	2	содержат иррациональные выражения, то умножим числитель
			x 9	3

и знаменатель на выражения, сопряженные числителю и знаменателю. Тогда

2

2

3

2

x 4

x 4

x 9

lim

x 4

0

lim

x 0

x 9 3

0

x 0

x 9 3

x 9 3

x 4 2

	.
		x 4 4								3		x			3					3
	lim						x 9				lim			x 9		lim			x 9			6			3	.
	x 0 x 9 9						x 4 2				x 0 x			x 4 2		x 0			x 4 2			4			2
	в). В выражении		3		3				при			имеем неопределенность вида												0	.
				1 x		1 x					x 0
																								0
					x

Чтобы получить разность кубов в числителе, умножим числитель и знаменатель

на неполный квадрат суммы 3 (1 x)2

1 x2

3 (1 x)2 . Тогда

3

3

(1 x) (1 x)

1 x

1 x

0

lim

lim

x

x 0

0

x 0

x

3

1 x

2

1 x

2

3

1 x

2

lim

2

2

.

x 0 3 x 1 2 3 1 x2 3 1 x 2

3

Пример 1.8. При x 1 функции

f (x)

1 x

и g(x) 1

являются бесконеч-

x

1 x

но малыми. Сравнить их.

Решение.

Функции f (x)

и

g(x)

элементарные.

Поэтому

lim

f (x) f (1) 0,

x 1

lim g(x) g(1) 0. Значит,

при x 1 функции

f (x)

и g(x)являются бесконечно

x 1

малыми.

Сравним их. Для этого вычислим

lim

f (x)

:

x 1 g(x)

1

f (x)

1 x

0

(1

) (1

)

x

2

x

x

lim

1.

lim

lim

lim

(1 x)

2

x 1 g(x)

x 1(1 x) (1

x)

0

x 1 (1 x) (1 x)

x 1

Так как lim

f (x)

1, то функции

f x

и g x

– эквивалентные бесконечно малые

x 1 g(x)

функции при x 1. Это записывают так:

f x g x при x 1.

Пример1.9.Сравнитьбесконечномалыефункции f (x) tgx

и g(x) x2 при x 0.

Решение. Для того чтобы сравнить две бесконечно малые функции, вычислим

lim f (x) . Воспользуемся следствием из первого замечательного предела:

x 0

tgx

1. Тогда

f (x)

0

tgx

tg x 1

и функция g(x) есть

lim

lim

lim

lim

0

2

x 0 x

x 0 g(x)

x 0 x

x 0 x x

бесконечно малая функция более высокого порядка при x 0, чем функция f (x).

При отыскании пределов удобно пользоваться следующим утверждением:

8

предел отношения бесконечно малых функций не меняется при замене их на эквивалентные бесконечно малые.

Напомним эквивалентные бесконечно малые функции:

sin x ~ x,

tgx ~ x,

arcsin x ~ x, arctg x ~ x при x 0.

Пример 1.10. Вычислить пределы:

arctg3x

x sin3

а) lim

;

б) lim

x

; в)

lim(x tg5x) ctg8x.

x 0 arctg5x

x 0 (arctg

x)2 arcsin(x 23 x)

x 0

Решение. В примерах а), б)

имеем неопределенность

0

, в примере в) имеем

0

неопределенность 0 , но ее легко можно свести к

неопределенности

0

.

а). При x 0 имеем: arctg3x ~ 3x, arctg5x ~ 5x. Таким образом,

0

lim

arctg3x

lim

3x

3

.

5x

5

x 0 arctg5x

x 0

б). При x 0 имеем: sin3

~ 3

, arctg

~

,

arcsin(x 23

) ~ (x 23

). Поэтому

x

x

x

x

x

x

x sin3

0

x 3

x

x

lim

lim

0

x)2 arcsin(x 23 x)

x 0 (arctg

x 0 (

x)2(x 23 x)

3

1

1

x

.

lim

lim

x 0 3

3 x2 2

x 0 3 x2 2

2

x

в). lim(x tg5x) ctg8x 0 lim

x tg5x

0

.

x 0

x 0

tg8x

0

Разобьем данный предел на два и воспользуемся тем,

что tg5x ~ 5x , tg8x ~ 8x

при x 0. Таким образом, имеем:

lim

x

lim

tg5x

lim

x

lim

5x

1

5

3

.

8x

8

4

x 0 tg8x

x 0 tg8x

x 0

x 0

8x

8

1.4. Бесконечно большие функции.

Неопределенности

,

; ,

0;

Функция f x

называется бесконечно большой при x a,

если

lim f (x) .

x a

Пример 1.11. Вычислить пределы:

а)

lim

3x2 2x 1

;

б)

lim

x2 2x

;

x

2x 2

x x3 1

2n 2

n 2

n2 1

1 7n 2

n2 1

в) lim

; г)

lim

;

д)

lim

.

3 7n

n

3 n6 1 3n

n

n 3 n6 1 ncosn

Решение. Как известно, при отыскании предела отношения многочленов или иррациональных функций при x младшие степени можно отбросить:

9

а).

б).

в).

г).

3x2 2x 1

3x2

3

x .

lim

lim

lim

2x 2

x

x 2x

x 2

lim

x2 2x

lim

x2

lim

1

0.

x

3

1

3

x

x x

x x

2n 2

2n 2

lim

n2 1

lim

n2

lim

n 2n 2

lim

9n2

9.

2

2

3 n6

n

n 3 n6 1 3n

n

n

n n

7

n

1

49

1

49

n 2

7n

1 7

7n

lim

lim

lim

49.

n

n

3 7

n

n 1

n 1

1

7

1

n

7n

7

д). Иногда полезно вынести за скобки старшую степень в числителе и знаменателе:

																									2												2
								2													1												1
				n2 1 n											n2
																		1						1						1						1			22
																				n2												n2
lim													lim														lim													4.
n 3				6									n						1				1				n				1				1				1 0
			n		1 ncosn
														n2	3 1										cosn			3 1									cosn
																															n6
																			n6					n												n

При вычислении последнего предела воспользовались тем, что 1 бесконечно n

малая функция при n , а cosn ограничена, следовательно, их произведение

1	cosn есть бесконечно малая функция при n , то есть	lim	1	cosn 0.
n		n n

Пример 1.12. Вычислить пределы:

		x	3
а) lim					x ;
		2
			1
x x

б)		3	(x 1)	2		3	(x 1)	2
	lim								.
	x

x3

Решение. а). lim

x x2 1

3

x

3

x

x

1

x

lim

x

lim

lim

0.

2

2

x

1

x x

x x

x

б). Имеем неопределенность вида . Для ее раскрытия умножим и разделим выражение нанеполныйквадратсуммыи учтем,что (a b)(a2 ab b2) a3 b3 . Тогда

(x 1)2 (x 1)2

lim 3

(x 1)2 3 (x 1)2

lim

x

x 3 (x 1)4 3 (x2 1)2 3 (x 1)4

(x2

2x 1) (x2 2x 1)

4x

4

lim

lim

lim

0 .

x 3 (x 1)4 3 (x2 1)2 3

(x 1)4

x x4/3 x4/3 x4/3

x 3x1/3

1.5. Второй замечательный предел. Неопределенность 1

При раскрытии неопределенности 1 полезно использовать второй за-

мечательный предел:

			1	x	1/ y
	lim	1			lim 1 y	e	.
			x
	x				y 0

10