Matan__teoria

Федеральное агентство по образованию ГОУ ВПО «Уральский государственный технический университет − УПИ»

Учебное пособие

Научный редактор − проф., д(р физ.(мат. наук Е. Ф. Леликова

Екатеринбург

2007

1

УДК 517.2 : 517.3 ББК 22.161.1 М 62

Рецензенты:

кафедра математики Уральского государственного горного университета (зав. кафедрой, проф., д(р физ.(мат. наук В.Б. Сурнев); проф. д(р физ.(мат. наук И.В. Мельникова (Уральский государственный уни(

верситет им. А.М, Горького, кафедра математического анализа)

учебное пособие / Р.М.Минькова. Екатеринбург: ГОУ ВПО УГТУ(УПИ, 2007. 120 с.

ISBN 978(5(321(01006(8

Рассмотрены дифференцирование и экстремум функций нескольких пере( менных, интегрирование функций нескольких переменных (двойные, тройные, криволинейные, поверхностные интегралы), теория скалярного и векторного полей. Учебное пособие предназначено для студентов физических специально( стей физико(технического факультета.

Библиогр.: 7 назв. Рис.83.

Подготовлено кафедрой «Вычислительные

методы и уравнения математической физики»

при поддержке физико(технического факультета.

УДК 517.2: 517.3 ББК 22.161.1

ISBN 978(5(321(01006(8	© ГОУ ВПО «Уральский государственный
	технический университет − УПИ», 2007
	© Р.М.Минькова, 2007

2

1. Понятие функции нескольких переменных

……………..…..…………...……5

2.Предел и непрерывность функции …...........................……...…..……...…...…6

3.Дифференцирование функции ……...……………….……...…..……...……….8

3.1.Частные производные …….........................…………....….......……..…....8

3.2.Дифференцируемые функции ……..........………….......….....….....…....10

3.3.Дифференциалы.....................…………..…………….....….....…….……12

3.4.Сложные функции и их дифференцирование.........................……….…14

3.5.Дифференциалы сложной функции …...……….…..…..…....……….....16

3.6. Неявные функции и их дифференцирование	...........................................17
3.7. Формула Тейлора........................................................................................	22

4.Геометрические приложения …..........................................….....………....….23

5.Экстремумы функции ……….............………………………….....……....…..27

5.1.Локальный экстремум функции …........……..……….……...…….........27

5.2.Глобальный экстремум функции..................................................….....…31

5.3.Условный экстремум функции ……....…..…..…….….……...…............32

6.Понятие интеграла по фигуре и его свойства ….......................................….36

6.1.Фигура и ее мера …................……………………….....…....…….…....36

6.2.Задача о вычислении массы фигуры ….................................….……....37

6.3.Понятие интеграла по фигуре ……...............................…....…….….....37

6.4.Конкретные виды интегралов по фигуре ……............................……...38

6.5.Свойства интеграла по фигуре...........................…....….…...…....……..39

6.6.Механические приложения интеграла по фигуре ...…........….……….41

7.Вычисление интегралов по фигуре............………………………......………43

7.1. Определенный интеграл............................................................................

43

7.2.Криволинейный интеграл первого рода……...............................……...52

7.3.Двойной интеграл в прямоугольной системе.............................………54

7.4.Двойной интеграл в криволинейной системе …..........................……..58

7.5.Тройной интеграл в прямоугольной системе ...........................……….62

7.6.Тройной интеграл в криволинейной системе.................................……66

7.7.Поверхностный интеграл первого рода ….............................…....……70

.

8.Скалярное поле …….....................................................…...…...…….....….…73

8.1.Производная поля по направлению...................................................….74

8.2.Градиент скалярного поля и его свойства ……................…….…...…75

9.Векторное поле и векторные линии ………………..…….…...…..…......…77

10. Поток векторного поля............................………...…………..………...…...79 10.1. Задача о количестве жидкости …..............................…...……………79

10.2.Понятие потока и формы его записи …………………...……...…….81

10.3. Вычисление потока …...............................……………...….…..……..81

3

10.4. Формула Остроградского. Дивергенция поля

.....................................85

11.Линейный интеграл и циркуляция векторного поля ……….……......……89

11.1.Задача о работе силы …....................................................................….89

11.2.Понятие линейного интеграла и его свойства …................................89

11.3.Вычисление линейного интеграла …...........................................……90

11.4.Формулы Грина и Стокса. Ротор поля............………...…...…...........92

11.5. Условия независимости линейного интеграла от формы пути ........	96
12. Некоторые классы векторных полей.............................................................	99
12.1. Потенциальное поле..............................................................................	99
12.2. Соленоидальное поле..........................................................................	102
12.3. Гармонические поля............................................................................	105
13. Повторные операции теории поля..............................................................	107
14. Оператор Гамильтона..................................................................................	108
15. Теория поля в ортогональной криволинейной системе...........................	110
15.1. Криволинейная система координат и ее базис.................................	110
15.2. Основные характеристики поля в ортогональных координатах....	112
Библиографический список……………………………………...………........119

4

Рассмотрим линейное пространство		Rk , элементы (точки) которого
M (x1, x2 ,..., xk )	есть совокупности из k чисел. Введем ряд понятий.
1).	между точками M (x1, x2 ,..., xk )	и N (y1, y2 ,..., yk ) пространства Rk

определим по формуле

ρ (M, N ) = (x1 − y1)2 + (x2 − y2)2 +...+ (xk − yk )2 .

2). Последовательность		точек M n назовем		к
точке M при n → ∞ , если ρ (Mn ,M ) → 0			при n → ∞ .
3).	точки M0 радиуса r		назовем множество
	Sr (M0) = {M Rk : ρ (M0 ,M ) < r }.
Например, на плоскости		XOY окрестность точки		M0 есть
круг с центром в точке M		0 радиуса r (рис. 1).		Рис.1

точки M0 радиуса r назовем множество

Sr (M0) = Sr (M0) \ {M0} = {M Rk : 0 < ρ (M0 ,M ) < r }.

4). Точку M0 из множества D назовем (рис.2), если она принадлежит множеству D с некоторой своей окрестностью.

5). Точку P0 из множества D назовем (рис.2) , если в любой ее окрестности содержатся точки, как принадлежащие множеству D , так и не принадлежащие множеству D .

6). Множество D назовем		, если любая его точка яв(
ляется внутренней (рис.1).			Рис.2
7). Множество D назовем		, если оно содержит все
свои граничные точки (рис.2).
8). Множество D назовем		(рис.2), если оно содержится в неко(
торой окрестности конечной точки. В противном случае множество
назовем	(например, первая четверть на плоско(
сти).
9). Множество D назовем		, если любые его две точки мож(
но соединить линией, лежащей в этом множестве ( например, мно(
жество на рис.3, состоящее из дуги и окружностей, не является
связным; оно имеет четыре компоненты связности).			Рис.3
10). Открытое (замкнутое) связное множество назовем открытой
(замкнутой)	.
	Функцией	k переменных называют отображение,	которое
каждой точке M (x1, x2 ,..., xk )		из множества D пространства Rk ставит в соответ(

ствие действительное число u . При этом принята запись u = f (M ) = f (x1, x2 ,...xk) , а множество D называют областью определения функции f .

5

Приведем простейшие примеры функций нескольких переменных.

1. Объем прямого кругового цилиндра V = π R2H есть функция двух перемен( ных R и H . Область определения этой функции {R > 0, H > 0} есть открытое не( ограниченное множество.

2. Функция z = x2 + y2 есть функция переменных x и y , определенная на всей плоскости OXY . Графиком этой функции называется множество точек (x, y,z),

координаты которых удовлетворяют			уравнению z = x2 + y2 , т.е.				z
график функции есть параболоид (рис. 4).
3. Функция	u = ln (1− x2 − y2 − z2)	является функцией трех пере(
менных x,	y, z , определенной на множестве x2 + y2 + z2 <1. Гео(						y
метрическое изображение функции трех переменных с помо(
щью ее графика невозможно, так как для этого потребова(
лось бы четырехмерное пространство.				x		Рис. 4
	2. Предел и непрерывность функции
Предел функции нескольких переменных обобщает понятие предела
функции одной переменной.
	Конечное	число	b называется пределом				функции

u = f (x1, x2,..., xk) = f (M) при M → M0 , если для любой последовательности точек

Mn , сходящейся к точке M0			(Mn ≠ M0) , соответствующие значения функции
f (Mn) сходятся к числу b , т.е.
		lim f (M) = b , если	f (Mn) →b при Mn → M0 (Mn ≠ M0 ).
		M →M0
Можно дать и другое				предела:
			δ > 0 такое, что f (M ) Sε (b)
	lim f (M) = b , если для ε > 0				для M Sδ (M0)		.
	M →M0
Для функции двух переменных используют и другую запись:
		lim	f (M) = lim f (x, y) = b .
		M →M0		x→x0
				y→y0
Из определения следует, что предел b				не зависит от способа приближения точ(
ки M к точкеM0 .

Свойства пределов функции одной переменной остаются справедливы( ми и для функций многих переменных.

1). lim	x + y −1	=	0 + 2 −1		= 1 .
x→0 x2 + x y2 + 3 0 + 0 + 3					3
y→2

В этом примере мы воспользовались тем, что предел элементарной функции в области ее определения равен значению функции в точке.

6

2). lim sin(xy) = lim			sin(xy) x =1 3 = 3.
x→3	y	xy→0	xy
y→0		x→3

Здесь мы воспользовались первым замечательным пределом.

3). lim x sin				1	= 0.
				y
x→0
y→0
	x y	2					y	2
4). lim					= lim	x				= 0 .
							x2 + y2
x→0 x2 + y2					x→0
y→0					y→0

В примерах 3 и 4 мы воспользовались тем, что x есть бесконечно малая функ(

	ция, функции sin	1	,	y2	есть ограниченные функции (по модулю не больше
		y		x2 + y2

единицы), а произведение бесконечно малой функции на ограниченную функ( цию есть бесконечно малая функция.

5). lim

x

3

+ y

3

=

x = ρ cosϕ

= lim

ρ3 (cos3ϕ + sin3ϕ )

= lim ρ

(cos3ϕ + sin3ϕ )= 0 .

x→0 x2 + y2

y = ρ sinϕ

ρ→0

ρ2

ρ→0

y→0

6). lim

x y

не существует, т.к. функция

f (x, y) =

x y

стремится к разным

x2 + y2

x→0 x2 + y2

y→0

числам при различных способах приближения точки (x, y) к точке (0,0):

при x = y имеем

lim

x y

= lim

y2

= 1

,

x=y→0 x2 + y2

y→0 2 y2

2

при x = 2y имеем

lim

x y

= lim

2 y2

=

2 .

x=2 y→0 x2 + y2

y→0 5 y2

5

Функция f (M ) называется

в точке M0 , если

lim

f (M ) = f (M0 ) .

M →M0

Свойства функции, непрерывной в точке, также переносятся с функции одной переменной на функцию нескольких переменных.

1). Функция f (x, y) =

x y2

− элементарна и поэтому непрерывна во всех точках,

x2 + y2

кроме точки (0,0), где функция не определена.

x y2

2

+ y

2

≠ 0 непрерывна в точке (0,0), так как

2). Функция f (x, y) =

, x

x2 + y2

0,

x

2

+ y

2

= 0

(см. пример 1.1) lim f (x, y) = 0 = f (0,0).

x→0

y→0

3). Функция f (x, y) =

1

− элементарна и поэтому непрерывна во всех точках,

y − x2

7

кроме точек линии y = x2 , где функция не определена.

Функцию f (M ) называют D , если она непрерывна

в каждой точке этой области.

Аналогично свойствам функции одной переменной, непрерывной на отрез( ке, формулируются свойства функции нескольких переменных, непрерывных в ограниченной замкнутой области.

	Пусть функция f (M )
	D Тогда
1)	функция f (M )	ограничена в области D , т.е.				f (M )				≤ K в области D ;
2)	функция f (M ) достигает в области D наибольшего и наименьшего значений;
3)	функция f (M )	принимает в области D все промежуточные значения между
	наибольшим и наименьшим значениями;
4)	функция f (M )			в области							D , т.е. для любого
	ε > 0 существует δ > 0 такое, что			f (M′)− f (M′′)				< ε			для любых точек
	M′, M′′ из области D , расстояние между которыми меньше δ .

3.Дифференцирование функции

3.1.Частные производные

Для простоты записи ограничимся функцией двух переменных f (x, y) . Вве( дем функции

f (x, y) = f (x + x, y + y) − f (x, y)

и функции по x и y:

x f (x, y) = f (x + x, y) − f (x, y), y f (x, y) = f (x, y + y) − f (x, y).

fx′(x, y) , fy′(x, y) функции f (x, y) называются пределы

	fx′	(x, y) = lim	x f (x, y)		,
				x
		x→0
Приняты и другие обозначения:				∂ f (x, y)		,
				∂x

	fy′ (x, y) = lim		y f (x, y)	.
			y
		y→0
∂ f (x, y)		. Частные производные функ(
	∂y

ции любого числа переменных определяются аналогично.

Так как в определении, например, производной fx′ при вычислении x f изменяется только x при неизменных других переменных, то справедливо сле( дующее

При дифференцировании функции по одному из ее аргументов, остальные аргументы считаются постоянными.

1) u = x3 sin y u′x = 3x2 sin y , u′y = x3 cos y ,

8

2)	u = e			2x+3 y + ln z u′x = e2x+3y 2, u′y = e2x+3y 3, u′z = 1 ,
								z
3)	z = x y z′x = y xy−1, z′y = xy ln x .
Отметим два момента.
1). Из непрерывности функции							существование частных производ(
ных	(						).	Например, функция
f (x, y) =			x			+ y непрерывна в точке (0,0), но производная		fx′ (0,0) не существует.

2). Из существования частных производных функции нескольких переменных

непрерывность функции (										).
			x y			, x	2	+ y	2	≠ 0
Например, функция			2	+ y	2
	f (x, y) = x									имеет частные производные в
			0,			x	2	+ y	2	= 0

точке (0,0), т.к. f ′

(0,0) = lim

x f (0,0)

= lim

f (0 + x,0)− f (0,0)

= lim

0− 0

= 0

x

x→0

x

x→0

x

x→0 x

и аналогично fy′ (0,0) = 0; но функция

f (x, y)

разрывна в точке (0,0), так как

lim

x y

не существует, как показано в примере 2.1.

x2 + y2

x→0

y→0

Частные производные fx′ (x, y) и fy′ (x, y)

являются функциями от x , y и от

них можно снова находить частные производные по

x

и y . Они называются

частными производными второго порядка:

fxx′′ = ( fx′)′

, fxy′′ = ( fx′

)′ ,

fyx′′

= ( fy′ )′ ,

fyy′ = (fy′ )′ .

x

y

x

y

∂2 f

∂2 f

∂2 f

∂2 f

Другие обозначения этих же производных:

,

,

,

∂y2 .

∂ x2

∂x∂y

∂y∂x

Аналогично определяются и частные производные более высоких порядков, например, fx′′′y x = ( fx′ y)′x .

Производные, в которых идет дифференцирование по различным перемен(

	′′	′′	′′
ным, называются смешанными, например, fx y ,		fy x ,	fx y x . Не доказывая, отме(
тим, что	, в случае ее непрерывности,
	, например, fy′′x =	fx′′y ,	fx′′′y x = fx′′′x y = fy′′′x x .

Требование непрерывности смешанных производных существенно.

x3 y − x y3					2	+ y		2	≠ 0
Например, можно показать, что для функции f (x, y) =		,	x
	x2 + y2
	0,	x	2	+ y			2	= 0

смешанные		производные		′′	и	′′	разрывны в точке (0,0) и различны:
				fx y		fy x
f ′′	(0,0) = −1,	f ′′	(0,0) =1.
x y		y x

9

1). Показать, что

f

′′

= f ′′

для функции

f (x, y) = ex y2 .

xy

y x

Имеем: fx′

=

y

2

e

x y

2

,

fx′′y =

2

e

x y2 ′

= 2 ye

x y2

+ e

x y

2

y

2

2 x y ,

y

y

′

=e

x y2

2 x y ,

′′

x y2

′

x y2

3

x y2

2 x y = e

2 x y + e

2 y .

fy

fy x = e

x

2). Найти

fx′′′z x ,

fx′′′z z

для функции

f (x, y, z) = x y2z3 .

′

= y

2

z

3

,

′′

′

′

2

z

2

,

′′′

= 0 ,

′′′

=

2

z .

Имеем fx

fx z

= ( fx

)z

= 3 y

fx z x

fx z z

6 y

3.2. Дифференцируемые функции

Напомним, что функция одной переменной f (x) дифференцируема в точке x0 ,

если ее приращение в этой точке представимо в виде

f (x0) = A x +α x ,

где A = const , α = α ( x) есть функция бесконечно малая при x →0 . Аналогично, функция двух переменных f (x, y) называется в точке (x0, y0) , если ее полное приращение в этой точке представимо в виде

f(x0, y0) = A x+ B y+α x+β y	,	(3.1)

где A = const, B = const , α = α ( x, y), β = β ( x, y) есть функции бесконечно ма( лые при x →0, y →0.

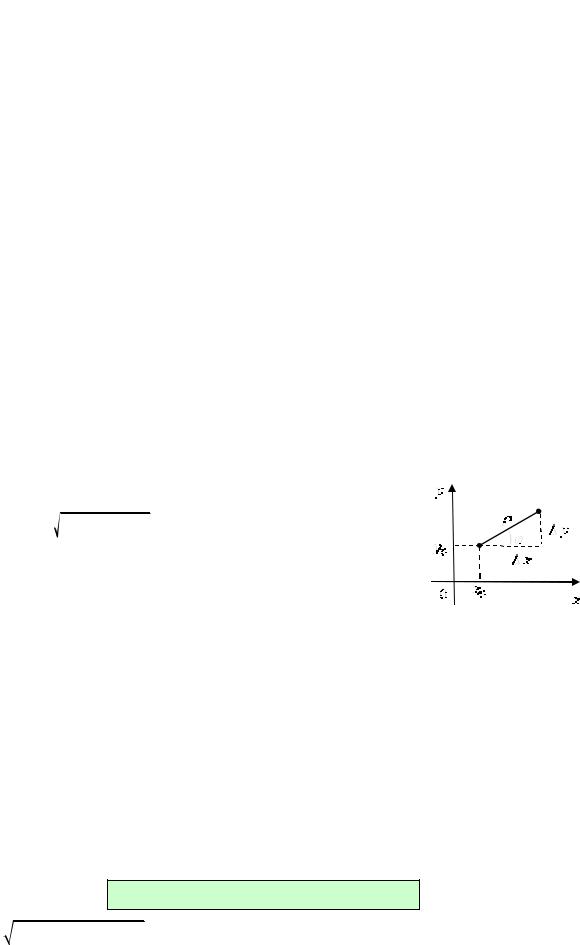
Для более компактной записи формулы (3.1) введем величину ρ = ( x)2 + ( y)2 (рис.5). Тогда

x = ρ cosϕ ,		y = ρ sinϕ ,
α x + β y = ρ (α cosϕ + β sinϕ ) = ρ γ ,
где γ = α cosϕ + β sinϕ . При этом,
если ρ →0, то	x →0,		α →0,	Рис.5
				γ →0.
	y →0,		β →0,

Поэтому равенство (3.1) можно переписать в следующем виде:

				f(x0, y0) = A x+ B y+ ρ γ	,	(3.2)
	где A = const, B = const , γ = γ (ρ ) есть функция бесконечно малая при ρ →0.
	Отметим, что lim	ρ γ	= 0, то есть ρ γ есть бесконечно малая более высокого
		ρ
	ρ→0

порядка, чем ρ : ρ γ = o(ρ ); поэтому равенство (3.2) можно переписать в виде

f(x0, y0) = A x+B y+o(ρ) .	.	(3.3)

Аналогично для дифференцируемой функции трех переменных

f (x0, y0, z0) = A x + B y + C z + o(ρ ) , где ρ = ( x)2 + ( y)2 + ( z)2 .

10