§22 Центральная симметрия.

Определение 22.1: Центральной симметрией с центром в точке О назовем такое преобразование плоскости, при котором каждая точка переходит в ( ), что .

Из 22.1 и 21.1 следует, что .

1) определяется заданием центра или пары соответствующих точек.

2) Формулы.

, ,

 (22.1)

3) - движение, т.к. .

4) Из свойства 5(§21) и =>

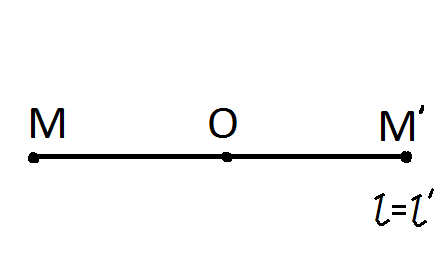а) б)

5) Инвариантной точкой является центр (свойство 6(§21), )

6) Множество центральной симметрии группы не образует, т.к. ,

7) Практическое использование :

может быть использована в задачах: на доказательство принадлежности трех точек одной прямой; на доказательство равенства фигур; на доказательство параллельности прямых; в которых рассматривается окружность, параллелограмм; на доказательство того, что четырехугольник- параллелограмм; на построения, сводящихся к построению отрезка с фиксированной серединой.

§23 Осевая симметрия.

Определение 23.1: Осевой симметрией называется такое ГПП, при котором каждая точка переходит в ( ) так, что и делится в ней пополам; точки оси переходят в себя.

1) однозначно определяется заданием оси или парой соответствующих точек .

2) Формулы.

(23.1),

3) - движение.

, ,

,

=> - движение.

4)

4.1)

=>

4.2)

4.3)

5) Инвариантными точками являются только точки оси симметрии.

6) - не группа, т.к. - перенос (если оси параллельны), или поворот (если оси пересекаются), или центральная симметрия (если оси перпендикулярны).

7) Из свойств 1-7 следует, что может использоваться в задачах: на доказательство равенства фигур; в которых рассматривается равнобедренный треугольник, ромб, квадрат, равносторонний треугольник; на построения, сводящиеся к построению отрезка с серединой на данной прямой и перпендикулярно данной прямой.

§24 Скользящая симметрия.

Определение 24.1: Композиция параллельного переноса и осевой симметрии с осью, параллельной вектору переноса, называется скользящей симметрией.

Из определения 24.1 следует, что середина лежит на .

1) Способы задания:

однозначно определяется заданием оси и вектора переноса .

2) Формулы:

,

, (24.1)

Используя метод координат и формулу (24.1), можно показать, что преобразование - коммутативно:

.

3) - движение, т.к. композиция двух движений- движение.

4) Взаимное расположение соответствующих прямых определяется взаимным расположением прямых при переносе и осевой симметрии.

5) Инвариантные точки:

, если , то система решений не имеет,

т.е. инвариантных точек не имеет.

6) - не образует группы, т.к. - не группа.

7) может использоваться в задачах: на доказательство равенства фигур; на построение различного рода орнаментов.

§25 Классификация движений плоскости (теорема Шаля).

Теорема Шаля: Любое движение плоскости есть или перенос, или поворот, или центральная симметрия, или осевая симметрия, или скользящая симметрия.

В основу доказательства теоремы положим теорему (19.1) и пусть:

, , тогда , тогда, на основе теоремы (19.1) существует два и только два движения, в которых и . И дальнейшие рассуждения сводятся к поиску этих движений. Найдем их, рассмотрев для этого различные случаи взаимного расположения точек .

1)

2)

3)

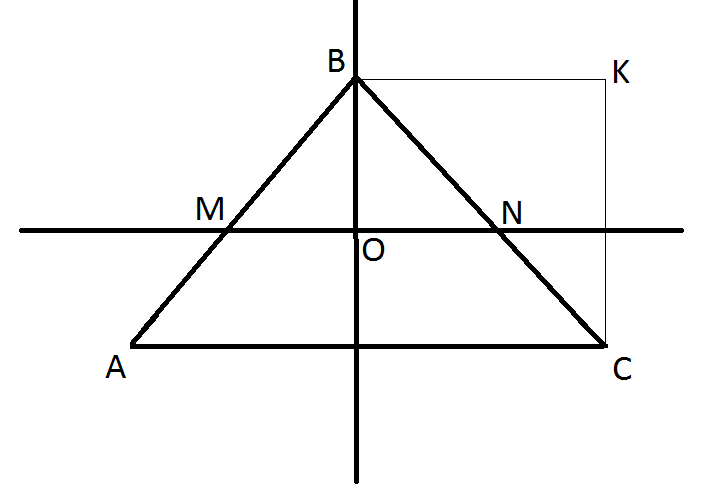
, т.к. =>

Вывод:

Следствия:

1) Любое движение плоскости представляет собой композицию не более трех осевых симметрий.

2) Любое движение первого рода есть или перенос, или поворот, или центральная симметрия.

3) Любое движение второго рода есть или осевая симметрия, или скользящая симметрия.

4) Любое движение первого рода можно представить композицией двух осевых симметрий.

5) Любое движение второго рода есть или осевая симметрия, или композиция трех осевых симметрий.

6) Осевая и скользящая симметрии являются движением второго рода.