27. Необходимое условие экстремума дифференцируемой функции:

Необходимое условие экстремума функции в точке : если f(x) дифференцируема в точке С и имеет в этой точке локальный экстремум, то   Таким образом, экстремум дифференцируемой функции следует искать лишь в тех точках, где производная равна нулю. Такие точки называются стационарными. Заметим, что если точка стационарна, то отсюда, вообще говоря, не следует, что в этой точке функция достигает экстремума, т.е. указанное необходимое условие экстремума функции не является достаточным (для f(x)=x3 в точке х=0 экстремума нет, однако  ).

Теорема 1. (первое достаточное условие экстремума дифференцируемой функции).

Пусть функция y=f(x).

1) дифференцируема всюду в некоторой окрестности т. С.

2) т. С - стационарная, т.е. f '(c) = 0, тогда  а) если существует окрестность, в которой производная  f '(x) положительна (отрицательна) слева от точки С и отрицательна (положительна) справа от точки С, то функция f(x) имеет в т. С локальный максимум (минимум)  (рис. 1,2);

б) если же производная  f '(x) имеет один и тот же знак слева и справа от точки С, то экстремума в т. С нет (рис.3,4).

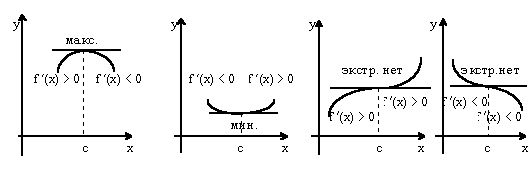    Рис.1                              Рис.2                             Рис.3                        Рис.4

Доказательство. Докажем теорему для точки максимума. Пусть  f '(x) положительна в окрестности слева от точки С и отрицательна справа от точки С.  . Обозначим через х₀ -любое значение аргумента из окрестности х₀>С. На сегменте [C,x₀] функция f(x) дифференцируема, следовательно, и непрерывна, поэтому по теореме Лагранжа

 ,     (1)

где   - некоторое значение аргумента между точками С и х₀.

 Аналогично рассматривается случай х₀<C.

 При х₀>С  , поэтому f(C)>f(x₀). Это и означает, что в точке С  f(x) имеет локальный максимум.

Теорема 2. (второе достаточное условие экстремума).

 Пусть функция y=f(x)

1) имеет производную всюду в некоторой окрестности т. С;

2) т. С - стационарная: f(x)=0;

3) имеет конечную вторую производную в т. С.

 Тогда, если  , то в т. х=С  f(x) имеет локальный максимум, если же    то в точке х= С f(x) имеет локальный минимум.

Замечание. Теорема 2 не дает ответ о наличии экстремума в том случае, когда    или не существует в т. х= С. В этом случае поведение функции в т. С следует изучить с помощью первого достаточного условия экстремума.

28. Стационарные и критические точки. Достаточные условия экстремума:

Стационарные точки- это точки, в которых производная функции равна 0 или не существует.

Находим производную и приравниваем ее к нулю.

Критической точкой дифференцируемой функции  , где   — область в  , называется точка, в которой все её частные производные обращаются в нуль. Это условие эквивалентно обращению в нуль дифференциала функции в данной точке, а также равносильно горизонтальности касательной гиперплоскости к графику функции. Это условие является необходимым (но не достаточным) для того, чтобы внутренняя точка области могла быть точкой локального минимума или максимума функции.

По теореме Ферма достаточное условие экстремума f'(x0)=0. Значит, для того чтобы найти точки «подозрительные» на экстремум, нужно взять производную от функции f(x0), приравнять ее к нулю и решить получившееся уравнение. Однако, не все корни этого уравнения будут экстремумами. Для того чтобы выяснить наверняка, является ли точка точкой экстремума, нужно знать достаточное условие экстремума.

Корни уравнения f'(x0)=0 называют стационарными точками.

Достаточное условие экстремума - если при переходе через стационарную точку производная меняет знак, то эта точка является экстремумом. Если меняет знак с «+» на «-», то это точка максимума. Если меняет знак с «-» на «+», то это точка минимума.

Если при переходе через стационарную точку производная не меняет знак, то эта точка не является экстремумом.

Очевидно, что точки, в которых функция принимает максимальное значение на некотором промежутке нужно искать среди точек максимума. А точки, в которых функция принимает минимальное значение - среди точек минимума. Однако нельзя забывать, что максимальное (минимальное) значение функция может принимать и на концах промежутка.

Для нахождения максимального или минимального значения функции применяют следующий алгоритм:

1. Берем производную от функции.

2. Находим стационарные точки, решая уравнение f'(x0)=0.

3. Проверяем достаточное условие экстремума. Выбираем те точки, в которых это условие выполняется.

4. Вычисляем значения функции в найденных точках и на концах промежутка. Самое маленькое значение будет минимальным значением функции на этом промежутке. А самое большое – максимальным.