- •2.1. Свойства степенной функции с нечетным положительным показателем.
- •2 .2. Свойства степенной функции с четным положительным показателем.
- •2.4. Свойства степенной функции с четным отрицательным показателем.
- •2.2. Свойства функции логарифма с основанием большим единицы.
- •Вопрос 16. Производная константы, суммы, произведения и частного.
Билет 1. Постоянные и переменные величины. Множество действительных чисел. Определения. Свойства. Свойства функций.
В технике и практике при изучении различных процессов и явлений приходится встречаться с различными величинами. К ним относится путь, время, скорость, ускорение, вес, сила, емкость, объем и т.д.
Во введении в анализ мы будем рассматривать величины, которые характеризуются одним или многими действительными числами, называемыми числовыми значениями величины.
Опред.1: Постоянной называется такая величина, которая в рассматриваемом процессе и явлении принимает одно и то же численное значение (скорость равномерного движения, вес тела, сумма углов треугольника в евклидовой геометрии).
Опред.2: Переменной называется такая величина, которая в рассматриваемом процессе или явлении принимает различные значения (скорость в неравномерном движении, сила переменного тока).
Совокупность всех численных значений некоторой переменной величины есть некоторое переменное множество. Оно может состоять из чисел различного вида. Это зависит от характера переменной величины:
1) Количество жителей Москвы – целые положительные числа (натуральные), т.е. множество значений этой величины – множество натуральных чисел;
2) Нагрузка, которую может выдержать медная проволока до разрыва характеризуется числами от нуля, положит., целыми, рациональными, иррациональными: от 0 до Р;
3) Курс поезда Москва-Питер, если мы отсчитываем от Твери: множество значений – положительные и отрицательные числа;
4) Время отсчитываемое от определенного момента как в прошлое, так и в будущее – все время. Поскольку мы будем рассматривать величины, характеризующиеся действительными числами, то для них нам нужно множество действительных чисел.
.
|
Действительные |
|
|
Рациональные |
Иррациональные |
||
Целые |
Ноль |
Дробные |
Положительные |
Отрицат. |
+ |
- |
|
+ |
- |
Отметим два свойства действительных чисел:
1. Между множеством всех действительных чисел и множеством всех точек прямой существует взаимно однозначное соответствие. (Каждой точке соответствует одно число и каждому числу соответствует одна точка).
2. Между любыми двумя различными действительными числами А и В содержится бесконечное множество действительных чисел, в этом легко убедиться рассматривая среднее арифметическое чисел.
Определение: Множество всех действительных чисел между a и в включая a и в, называется отрезком [а;в].
Определение: Множество всех действительных чисел между a и в, исключая а и в, называется интервалом (а;в).
Определение: Числовой отрезок действительных числам, в котором исключен а или в, называется полуотрезком или полуинтервалом (а; в), (а; в).
Определение:
Множество всех действительных чисел
считается бесконечным интервалом,
называется бесконечным интервалом (-
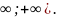
Во многих процессах и явлениях участвуют две или более переменных величины. При этом одна из них изменяется самостоятельно, а другие в зависимости от изменения первой. Поэтому одну из переменных величин мы будем называть независимой, или аргументом, понимая под этим, что ее численными значениями, мы можем распоряжаться по нашему усмотрению. Другую переменную величину мы будем называть функцией, т.к. она будет зависеть от 1-ой.
Определение: Переменная величина Y называется другой переменной величины Х, если существует закон с помощью которого для каждого рассматриваемого значения Х, взятого из множества Х (xєX), можно найти единственно соответствующее значение Y, из множества Y (yєY).
Переменная Х называется аргументом функции Y. у=f(х).
Выделим три основных составляющих определения функции:
1. Закон, указывающий как по взятому значению Х найти соответствующее значение У называется функциональным законом и обозначается f.
2. Множество Х всех рассматриваемых значений аргумента x называется областью определения функции, а множество У всех численных значений, которая принимает функция Х называется областью изменения функций.
3. Требование, чтобы каждому рассматриваемому значению х соответствовало лишь одно значение у, называется условием однозначности функции.
Определение: Пусть формулой задана функция у=f(х), имеющая своей областью определения которой отрезок, интервал или полуинтервал.
у







 у2
у2
 у1
у1
не
функция
у1
у1
не
функция


 х
0
у = f(x)
х
0
у = f(x)
х1 х2 а х1 х2 в
График функций f(х) – множество плоскости с координатами х и f(х).
Способы задания функции.
Существует три основных способа задания функции:
1. аналитический;
+ использование математического аппарата возможно, почти всегда можно точно определить х и у,
- нет наглядности.
2. графический;
+ наглядность
- неточность, нельзя применить математический аппарат для исследования.
3. табличный – функция задается таблицей, в одной строке аргумент, в другой у.
-
х
х1
х2
…
хn
у
у1
у2
уn
Достоинство: мы знаем точное значение у.
Недостатки: нет наглядности, нельзя применить математический аппарат для использования поведения этой функции. Невозможно понять, как ведет себя функция между любыми ближними Х.
Основные свойства функции:
1. а) Функция f(x) называется ограниченной сверху в области своего определения, если существует такое число в, что для любого х из области определения f(x) ≤ в. Само число в называется верней гранью множества значений функций.
у = 1 – х2 (Значение х = 1)
б) Функция f(x) называется ограниченной снизу в области своего определения, если существует такое число А, что для любого х из области определения f(x) ≤а. Само число а называют нижней гранью множества значений функции.
в) Если функция ограничена и сверху, и снизу, мы ее будем называть ограниченной, если она не ограничена хотя бы с одной стороны, она не ограничена.
2. Функция f(x) называется монотонно возрастающей, если для любых значений х1 и х2 из области определения х1< х2, выполняется условие f(x1) < f(x2).
Если для любых значений х1 и х2 из области определения х1< х2, выполняется условие f(x1) ≤ f(x2), она называется неубывающая.
Если для любых значений х1 и х2 из области определения х1< х2, выполняется условие f(x1) > f(x2), она называется убывающая.
Если для любых значений х1 и х2 из области определения х1> х2, выполняется условие f(x1) ≥ f(x2), она называется невозрастающая.
3. Функция у = f(x) называется четной, если для любых х из области определения f(-x) = f(x).
Пример: y = x2; y = cos xy
Функция нечетная, если для любых x, хєD, f(-x) = -f(x).
Главная особенность четных функций – Симметрия относительно оси У
График нечетных функций симметричны относительно начала координат.
4. Функция у = f(x) называется периодической, если существует такое число Т, не равное нужно, что для любого х, f(x + T) = f(x).
Периодом функции называется самое маленькое положительное значение Т.
Пример: sin (x) = y; T = 2 П.
Билет 2. Основные элементарные функции и их свойства.
1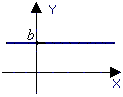 )
Функция
вида y = c, c = const;
)
Функция
вида y = c, c = const;
Постоянная функция- функция, заданная формулой у=c, где b-некоторое число. Графиком постоянной функции у=c является прямая, параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат.
2)Функция вида y = xn. Степенная функция.
1. Определение: Степенной функцией с вещественным показателем a называется функция y = xn , x > 0.
2 .
Свойства и графики:
.
Свойства и графики:
2.1. Свойства степенной функции с нечетным положительным показателем.
Область определения:.
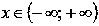 .
.Область значений:
 .
.Функция нечетная, так как
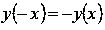 .
.Функция строго монотонно возрастает в области
определения функции.
Функция выпуклая при
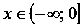 и вогнутая при
и вогнутая при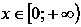 .
.
Точка (0;0) является точкой перегиба.
Функция проходит через точки (-1;-1) , (0;0) , (1;1) .
2 .2. Свойства степенной функции с четным положительным показателем.
Область определения:
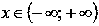 .
.
Область значений:
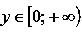 .
.
Функция четная, так как
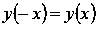 .
.
Функция возрастает при
 ,
убывает при
,
убывает при
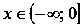 .
.
Функция вогнутая при
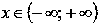 .
.
Точек перегиба нет.
Функция проходит через точки (-1;1) , (0;0) , (1;1) .
2 .3.
Свойства степенной функции с нечетным
отрицательным показателем.
.3.
Свойства степенной функции с нечетным
отрицательным показателем.
Область определения:
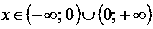 .
Область значений:
.
Область значений:
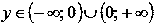 .
.
Функция нечетная, так как
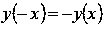 .
.
Функция убывает при
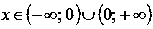 .
.
Функция выпуклая при
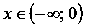
и вогнутая при
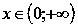 .
.
Точек перегиба нет.
Функция проходит через точки (-1;-1) , (1;1) .
2.4. Свойства степенной функции с четным отрицательным показателем.
О
 бласть
определения:
бласть
определения:
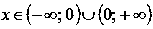
Область значений:
 .
.
Ф
 ункция
четная, так как
ункция
четная, так как
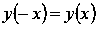 .
.
Функция возрастает
убывает
при
![]() .
.
Функция вогнутая при
 .
.
Точек перегиба нет.
Функция проходит через точки (-1;1) , (1;1) .
3)
Функция вида y = ax. Показательная
функция.
1.При
a > 0, a
![]() =
1, определена функция y = ax,
отличная от постоянной. Эта функция
называется показательной функцией с
основанием a.
=
1, определена функция y = ax,
отличная от постоянной. Эта функция
называется показательной функцией с
основанием a.
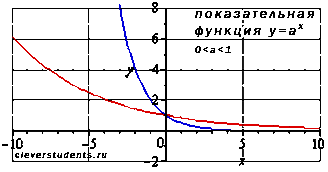
2.1.Свойства показательной функции с основанием меньшим единицы.
Область определения:
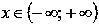 .
.
О
 бласть
значений:
бласть
значений:
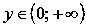 .
.
Функция не является ни четной, ни нечетной,
то есть она общего вида.
Функция убывает при .
Функция вогнутая при
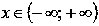 .
.
Точек перегиба нет.
Функция проходит через точку (0;1) .
2.2. Свойства показательной функции с основанием большим единицы.
О
 бласть
определения:
.
бласть
определения:
.
Область значений: .
Функция не является ни четной, ни нечетной,
то есть она общего вида.
Функция возрастает при
 .
.
Функция вогнутая при .
Точек перегиба нет.
Горизонтальной асимптотой является прямая y=0 при х стремящемся к минус бесконечности.
Функция проходит через точку (0;1) .
4) Функции вида y = logax. Логарифмические функции
Функция y = loga х (где а > 0, а =1) называется логарифмической.
2.1.Свойства логарифмической функции с основанием меньшим единицы.
О
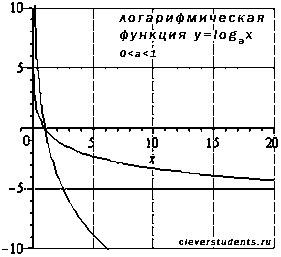 бласть
определения:
бласть
определения:
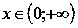
Область значений:
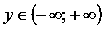 .
.
Функция не является ни четной, ни нечетной,
то есть она общего вида.
Функция убывает при .
Функция вогнутая при .
Точек перегиба нет.
Функция проходит через точку (1;0) .
2.2. Свойства функции логарифма с основанием большим единицы.
О
 бласть
определения:
бласть
определения:
Область значений: .
Функция не является ни четной, ни нечетной, то есть
она общего вида.
Функция возрастает при .
Функция выпуклая при .
Точек перегиба нет.
Функция проходит через точку (1;0) .
5) Тригонометрические функции.
1. Синус. Функция вида y=sin(x).
Область определения: .
Наименьший положительный период
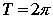 .
.
Функция обращается в ноль при
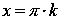 ,
где
,
где
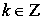 ,
Z – множество целых чисел.
,
Z – множество целых чисел.
О
 бласть
значений:
бласть
значений:
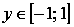 .
.
Функция синус - нечетная, так как
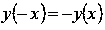 .
.
Функция убывает при
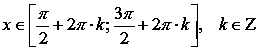 ,
возрастает
при
,
возрастает
при
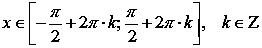 .
.
Функция имеет локальные максимумы в точках
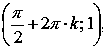 ,
локальные
минимумы в точках
,
локальные
минимумы в точках
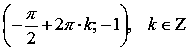 .
.
Функция вогнутая при
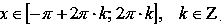 ,
выпуклая
при
,
выпуклая
при
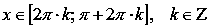
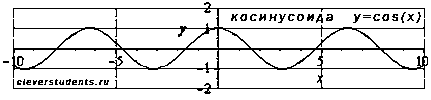
2. Косинус. Функция вида y = cos(x).
Область определения: .
Наименьший положительный период косинусоиды .
Функция обращается в ноль при
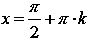 ,
где
,
Z – множество целых чисел.
,
где
,
Z – множество целых чисел.
Область значений: .
Функция косинус - четная, так как
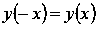 .
.
Функция убывает при , возрастает при .
Функция имеет локальные максимумы в точках
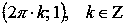 ,
локальные
минимумы в точках
,
локальные
минимумы в точках
 .
.
Функция вогнутая при выпуклая при .
Координаты точек перегиба
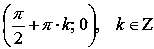 .
.
3. Тангенс. Функция вида y = tg(x).
Область определения :
 ,
где
,
где
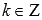 ,
Z – множество целых чисел.
,
Z – множество целых чисел.Н
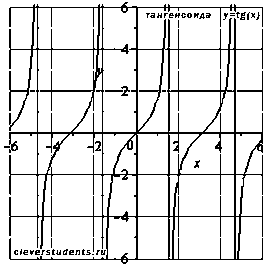 аименьший
положительный период тангенсоиды
аименьший
положительный период тангенсоиды
 .
.
Функция обращается в ноль при , где
Z – множество целых чисел.
Область значений: .
Функция тангенс - нечетная, так как .
Функция возрастает при
 .
.
Функция вогнутая при
 ,
выпуклая
при
,
выпуклая
при
 .
.4. Котангенс. Функция вида y = ctg(x). Область определения:
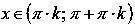 ,
где
,
Z – множество целых чисел.
Наименьший
положительный период
.
,
где
,
Z – множество целых чисел.
Наименьший
положительный период
.
Функция обращается в ноль при , где
 ,
Z – множество целых чисел.
,
Z – множество целых чисел.
О
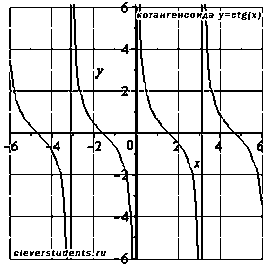 бласть
значений функции котангенс:
.
бласть
значений функции котангенс:
.
Функция нечетная, так как .
Функция убывает при
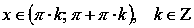 .
.
Функция котангенс вогнутая при
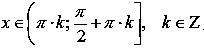 ,
выпуклая
при
,
выпуклая
при
 .
.
Координаты точек перегиба .
6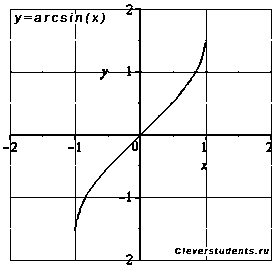 ).
Обратно тригонометрические функции.
1. Арксинус. Функция вида y=arcsin(x).
).
Обратно тригонометрические функции.
1. Арксинус. Функция вида y=arcsin(x).
Область определения арксинуса:
 .
.
Область значений функции арксинус:
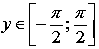 .
.
Функция нечетная, так как .
Функция возрастает на всей области определения,
то есть, при .
Функция вогнутая при
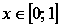 ,
выпуклая при
,
выпуклая при
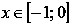 .
.
Т
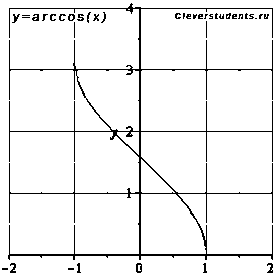 очка
перегиба (0; 0) , она же ноль функции.
очка
перегиба (0; 0) , она же ноль функции.
2. Арккосинус. Функция вида y = arcos(x).
Область определения арккосинуса: .
Область значений арккосинуса:
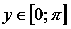 .
.
Функция не является ни четной ни нечетной, то есть,
она общего вида.
Функция убывает на всей области определения, то
есть, при .
Функция вогнутая при , выпуклая при
Точка перегиба
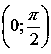 .
.
3 .
Арктангенс. Функция вида y =arctg(x).
.
Арктангенс. Функция вида y =arctg(x).
Область определения: .
Область значений:
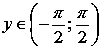 .
.
Функция арктангенс - нечетная, так как .
Функция возрастает на всей области определения, то есть, при .
Функция арктангенс вогнутая при
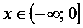 ,
выпуклая при
,
выпуклая при
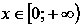 .
.
Т
 очка
перегиба (0; 0) , она же ноль функции.
очка
перегиба (0; 0) , она же ноль функции.
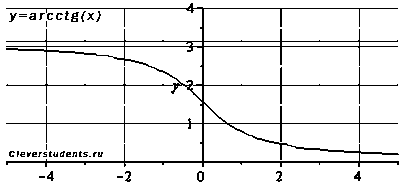
4.Арккатангенс. Функция вида y=arcctg(x).
Область определения: .
Область значений арккотангенса:
 .
.
Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
Функция убывает на всей области определения, то есть, при .
Функция вогнутая при , выпуклая при .
Точка перегиба .
Билет 3.. Сложные функции, взаимообратная функции, элементарной функции, алгебраические и трансцендентные.
Определение: обратная функция – пусть дана функция у = f(x), обратной по отношению к ней называют х = g(у), полученную из функции (1), для которой у – аргумент, а х – функция. Для того чтобы существовало единственная функция g(у) достаточно, чтобы у= f(x) была монотонной (или только возрастающей или только убывающей). У взаимообразной функции область определения функции и изменения функции меняются местами.
Если нам дана функция у = F(u), а само U = ρ(x), то функция у = F(ρ(x)) называется сложной функций.
Пример: у = sin x2, у = sin u, где u = x2.
Элементарной функцией называется функция, которая может быть задана с помощью одной формулы у = f(x), где справа стоящее выражение f(x) составлено из основных элементарных функций при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции.
Алгебраической функцией называется функция вида y=f(x), которая удовлетворяет уравнению P0(x)yn+ P1(x)yn-1+…+ Pn(x)y0=0, где P0(x), P1(x)… Pn(x) – некоторые многочлены, зависящие от х. Пример: ax2+bx+c.
Функция, не являющаяся алгебраической, называется трансцендентной. Пример: y=cosx, y=10x.
Билет 4. Числовая последовательность и её придел
Функций
целочисленного аргумента называется
y = f(n), аргумент которой принимает только
целые положительные значения (натуральные).
Все значения такой функции образуют
бесконечную совокупность чисел,
называется числовой последовательностью
(у1,
у2,
уn).
Сами числа называются членами
последовательности, а уn
– общий член последовательности. Зная
формулу общего члена, можно восстановить
его последовательность (y =
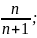 y1 =
y1 =
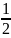 ; y2 =
; y2 =
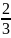 ; y3 =
; y3 =
 ; yn =
; yn =
 ;)
;)


.
График
такой функции – совокупность изолированных
точек (отдельных) бывает так, что члены
последовательности безгранично
приближаются к некоторому числу А, когда
n бесконечно возрастают. Это очень важный
случай и имеет особое название. Число
А называется пределом последовательности
при n
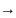 ∞, если каково бы ли было выбранное
число Е
∞, если каково бы ли было выбранное
число Е
 0, для него всегда найдется такой номер
N, что все члены последовательности,
начиная с номера n
N, будут удовлетворять неравенству (yn
- А)
Е. символически:
0, для него всегда найдется такой номер
N, что все члены последовательности,
начиная с номера n
N, будут удовлетворять неравенству (yn
- А)
Е. символически:
lim yn = А
n ∞
у
А
 +Е
+Е
А
А-Е
Х
N
-Е < yn – А < Е
А-Е < yn < А + Е
Билет 5. Предел функции на бесконечности и в точке. Односторонние пределы.
Если аргументы Х изменяются непрерывно, то функция называется функцией непрерывного аргумента. Пусть (J) функция y = f(х) задана на интервале (а; ∞) и х ∞. Опр.: число А называется приделом функции y = f(х) при х ∞, если какого бы ли было заранее нами выбранное положительное Е, для него найдется такое постоянное число х0, что для всех х, х ˃ х0 соответствующие значения функции y = f(х) будут удовлетворять неравенству (f(х) – А) < Е.
Определение предела при х - ∞
 у
у
А +Е
А
А-Е
х
х0
Относительно точки х0 называется любой интервал (а. в), серединой которого является точка х0. Очевидно, что любая точка х0 имеет бесчисленное множество окрестностей. Если длина окрестностей равна 2б, то интервал (х0 – б; х + б) называется дельтоокрестностью точки х0.
х0 – б х0 х0 + б
Число А называют пределом функции y = f(х) в точке х0, х х0, ели для любого Е, Е ˃ 0, найдется такое б, б ˃ 0, что для всех значений х, удовлетворяющих неравенству (х - х0) б, будет выполняться (f(х) - А) У. обозначение:
lim f(х) = А
n ∞
 у
у
А +Е
А
А-Е
х
х0
Односторонние пределы
Если
функция y = f(х) стремится к пределу А,
когда , х
(.) а при x<a/x>a только слева/ только
справа, то число а называют пределом
функции слева/справа.
 =A/
=A/ =A
=A
Билет 6. Некоторые теоремы о пределах.
1.Теорема: если какая-либо функция у = f(x) имеет предел А, при данном изменении x, то этот предел при одном и том же изменении х- единственен.(без доказат.)
2. Теорема: если функция у = f(x) стремится к пределу А:
1) при х→∞
2) при х→ -∞
3) при х→х0,
То эта функция будет ограниченна соответственно:
1)(х; +∞)
2)(- ∞; х)
3)в некоторой окрестности точки х0
При этом в любом случае предел А не может быть меньше любой нижней и больше любой верхней грани. (без доказат.)
3. Теорема: предел функции у = с при любом изменении х равен с
Билет 7. Бесконечно малые и бесконечно большие величины. Их взаимосвязь. Свойства бесконечно малых.
Функция
α= α(х) называется бесконечно малой при
х→а (х→∞), если предел
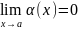
( )
(у=(х-1)2
)
)
(у=(х-1)2
)

Эта функция бесконечно малая при х = 1
Бесконечно большая при х→+∞/ х→ -∞
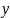 =
=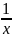
|
Это функция бесконечно малая при х→+∞ или х→ -∞ бесконечно большая и при х→0 у=0 – это функция бесконечно малая при любом изменении х. |
Опр. Функция у = f(х) называется бесконечно большой величиной при данной измени х модуль функции имеет бесконечный предел.
Отметим, что бесконечно малая и бесконечно большая величина носят локальный (местный характер).
Теорема:
если при некотором изменении х, функция
у = f(х)
будет бесконечно большой величиной,
то функция
=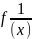 при том же изменении х, будет бесконечно
малой. Если функция α(х) есть бесконечна
(без док.) малая величина, не равная
тождественно 0, то 1/α(х) при том, же
изменении будет х бесконечно большой.
при том же изменении х, будет бесконечно
малой. Если функция α(х) есть бесконечна
(без док.) малая величина, не равная
тождественно 0, то 1/α(х) при том, же
изменении будет х бесконечно большой.
Свойства основные бесконечно малых
Алгебраическая сумма 2, 3 и вообще определенного числа (не стремится к бесконечности) бесконечно малых величин есть величина бесконечно малых.
Произведения бесконечно малой величины на ограниченную функцию при данном изменении х, есть величина бесконечно малая.
Произведение постоянной на бесконечно малую есть величина бесконечно малая.
Если функция f(х) и g(х) бесконечно малые, то их произведение тоже бесконечно малая величина.
Частное
 ,
где α(х) бесконечно малое, а предел z(х)
не равен нулю (
,
где α(х) бесконечно малое, а предел z(х)
не равен нулю (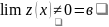 ),
а равен в, в = const, то такое частное –
есть бесконечно малая величина теорема
о связи функции с ее пределом: если
функции у
= f(х)
представляется в виде суммы у = в + α,
где в = const, а α – бесконечно малая
величина, то предел этой функции равен
в/
),
а равен в, в = const, то такое частное –
есть бесконечно малая величина теорема
о связи функции с ее пределом: если
функции у
= f(х)
представляется в виде суммы у = в + α,
где в = const, а α – бесконечно малая
величина, то предел этой функции равен
в/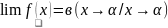 ,
если /
,
если /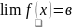
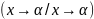 ,
то у = в +
,
то у = в +
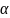 (функция отличается от своего предела
на величину бесконечно малую
(функция отличается от своего предела
на величину бесконечно малую
Билет 8.Основные теорема о пределах
1
теорема:
Предел суммы есть сумма пределов каждой
функции
 (u1
+ u2
+ … un)
= lim
u1
+ lim
u2
+ … lim
un
(u1
+ u2
+ … un)
= lim
u1
+ lim
u2
+ … lim
un
lim u1 а1; lim u2 = а2
Д оказательство:
lim
u1
а1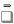 u1
=
а1
+
Е1
u1
=
а1
+
Е1
lim u2 а2 u2 = а1 + Е2 u1 + u2 = (а1 + а1) + (Е1 + Е2) lim(u1 + u2) = а1 + а1, чтд.
бесконечно малое
(lim
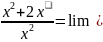 )
=
)
=
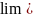 1
+
1
+
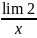 = 1 + 0 = 1
= 1 + 0 = 1
х→∞ х→∞ х→∞ х→∞
2 теорема: Предел произведения равен произведению пределов.
lim(U1*U2*Un)=limU1*limU2*Un
l imU1=a1; U1=a1+є1
limU2=a2;
U2=a2+є2
 U1*U2=
(a1+є1)(
a2+є2)=
a1*a2+
a1*є2+
a2*є1+
є1*є2=
a1*a2
U1*U2=
(a1+є1)(
a2+є2)=
a1*a2+
a1*є2+
a2*є1+
є1*є2=
a1*a2
lim(U1U2)=limU1*limU2
ЧТД.
Следствие: Постоянный множитель можно вынести за знак предела.
lim(U1*С)=limU1*limС=С*limU1 (C=const) ЧТД.
lim(5x2)=5limx2=5*42=80
3
теорема:
Предел частного
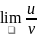 равен частному пределов
равен частному пределов
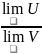 ,
если V<>0.
,
если V<>0.
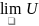 =a1
U
=
а1
+
Е1
=a1
U
=
а1
+
Е1
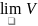 =a2
V
=
а2
+
Е2
=a2
V
=
а2
+
Е2
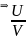 =
=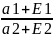 =
= +
-
+
- =
=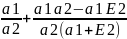 =
ЧТД.
=
ЧТД.
4
теорема:
Если
между соответствующими значениями трех
функций U=U(x),
V=V(x),
Z=Z(x)
выполняется неравенство U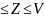 и при этом функции U(x)
и V(x)
при x
и при этом функции U(x)
и V(x)
при x и
и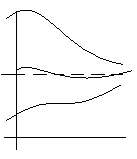 ли
x
ли
x ,
стремятся к одному и тому же пределу в
(
,
стремятся к одному и тому же пределу в
(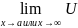 =b
и
=b
и
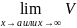 =b),
то
=b),
то
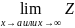 =b
предел Z(x)
равен b.
Принцип 2-х милиционеров.
=b
предел Z(x)
равен b.
Принцип 2-х милиционеров.
5
теорема:
Если
при
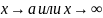 функция y(x)≥0
и стремиться y(x)
b,
то b>0.
функция y(x)≥0
и стремиться y(x)
b,
то b>0.
6
теорема:
Если
U(x)
и V(x)
имеют пределы при
и U ,
то limU<limV.
,
то limU<limV.
Билет 9. Первый замечательный предел.
Теорема:
Предел отношения sinx
к x,
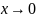 ,
равен 1.
,
равен 1.
 =1.
=1.
Рассмотрим сектор окружности радиусом 1, с центральным углом, равным Х.
B
C
(AC
|| BM,
AC
![]() OA,
x
- угол) – условие.
OA,
x
- угол) – условие.
 S
OAB)<S(cek
CAB)<S(∆OAC)
S
OAB)<S(cek
CAB)<S(∆OAC)
S OAB)=1/2MB*OA; |OA|=1; MB=sinx
MB/OB=sinx;
0 M A S(cek CAB)=1/2*r*величины угла в радианах;
S(cek CAB)=1/2*1*x; S(∆OAC)= ½*1*tgx
1/2sinx<1/2x<1/2tgx
Sinx<x<tgx
1<x/sinx<1/cosx
1>sinx/x>cosx
Cosx<sin/x<1.

Пример:
1)

2)
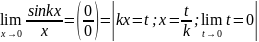 =
=
3)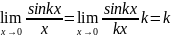
4)
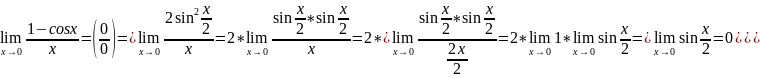
5)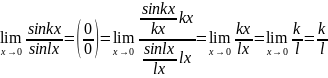
Билет 10. Второй замечательный предел.
Рассмотрим , где n=1,2,3…
Теоремы:
1.
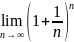 заключен между 2 и 3. За этот предел было
принято число е=2,7182818284…
заключен между 2 и 3. За этот предел было
принято число е=2,7182818284…
2. =е.
=е.
Доказательство:
Зная,
что второй замечательный предел верен
для натуральных значений x, докажем
второй замечательный предел для
вещественных x, то есть докажем, что
![]() .
Рассмотрим два случая:
.
Рассмотрим два случая:
1.
Пусть
![]() .
Каждое значение x заключено между двумя
положительными целыми числами:
.
Каждое значение x заключено между двумя
положительными целыми числами:
![]() ,
где
,
где
![]() —
это целая часть x.
—
это целая часть x.
Отсюда
следует:
![]() ,
поэтому
,
поэтому
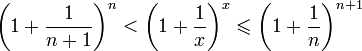 .
.
Если
,
то
![]() .
Поэтому, согласно пределу
.
Поэтому, согласно пределу
![]() ,
имеем:
,
имеем:
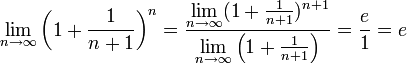
![]() .
.
По
признаку (о пределе промежуточной
функции) существования пределов
![]() .
.
2.
Пусть
![]() .
Сделаем подстановку − x
= t,
тогда
.
Сделаем подстановку − x
= t,
тогда
![]()
![]() .
.
Пример:
1.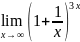 =
=
=
=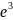
2.
 =
= =
=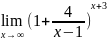 =
= =
=
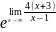 =
=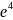
Билет 11. Непрерывность функции. Классификация точек разрыва.

Пусть y=f(x) определена в точке x=x0и в некоторой ее окрестности.
Пусть х получает приращение дельта х.
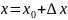
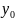
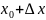
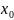


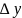 =f(
)-f(x)
=f(
)-f(x)
=f( )
Тогда y получает приращение ∆у. Тогда
Определение: Функция называется неразрывной в точке х0 если она определена в этой точке и некоторой ее окрестности и если предел у дельта у при ∆х --> 0 равен 0
или
Или
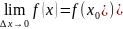
Y=x3 непрерывна в любой точке своей области определения. Для любого х0: у0=х03
Доказательство: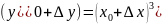
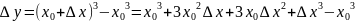

Функция непрерывна в точке х0, где х0произвольнаяточкаизобластиопределения, Функция непрерывна в любой точке области определения. Ч.т.д.
Теорема 1. Еслиf1(x) и f2(x) непрерывны в точке х0, то F(x) равная сумме этих функция также непрерывна в этой точке.
Доказательство.
Т.к.
f1(x)
непрерывна в точке х0
то:

Аналогично для f2(x).

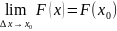 -
непрерывна. Ч. Т. Д.
-
непрерывна. Ч. Т. Д.
Следствие. Теорема справедлива для любого числа слагаемых.
Опираясь на свойства пределов, так же можно доказать следующие теоремы:
1)Произведение двух непрерывных функций так же непрерывная функция. 2) Частное двух непрерывных функций также является непрерывной функцией если знаменатель не равен 0.
3)если U=F(x) непрерывна в точке x0и f(U) непрерывна в точке u0=F(x0) то сложная функция f(F(x)) – также непрерывна в точке.
Используя эти теоремы можно доказать теорему 2
Теорема 2. Всякая элементарная функция непрерывна в своей области определения.
Определение. Если функция непрерывна в любой точке промежутка (a,b) то говорят что она непрерывна на этом промежутке.
Определение. Если функция непрерывна в точке х0 то:
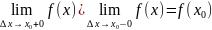
Если какое либо равенство не выполняется то функция разрывна в точке х0

Классификация точек разрыва.
1. Разраыв первого рода, или устранимый разрыв.
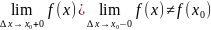
2 .Разрыв
второго рода – неустранимый разрыв.
.Разрыв
второго рода – неустранимый разрыв.
Происходит скачок.
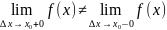

Функция терпит неустранимый разрыв –
Бесконечный скачок. Разрыв второго рода.
Б илет
12. Некоторые свойства непрерывных
функций.
илет
12. Некоторые свойства непрерывных
функций.
Теорема 1.Еслиf(x) непрерывна на (a,b) то найдется по крайней мере одна точка x1 на [a,b] такая что f(x1)=>f(x) для любого ч на [a,b], x1не равно x0и точка x2на [a,b]такая что f(x2),=f(x) для любых х на отрезке не равных x2
1)f(x1) наибольшее значение функции на данном отрезке.
2)f(x2) наименьшее.
Т еорема
2.
Пусть функция f(x)
непрерывна на [a,b]и
на концах отрезка принимает значение
разных знаков, тогда меду точками a
и b
найдется по крайней мере одна точка с
такая что
еорема
2.
Пусть функция f(x)
непрерывна на [a,b]и
на концах отрезка принимает значение
разных знаков, тогда меду точками a
и b
найдется по крайней мере одна точка с
такая что
f( c)=0 (может быть несколько точек.
Теорема 3. Пусть функция f(x) определена и непрерывна на [a,b] и пусть f(a)=A,f(b)=B,
A неравно B, тогда для любых m таких что A<m<B найдется такая с: a<c<b что f( c)=m.
Следсвие. Если функция заключена нерперывна на интервале (a,b)и принимает наибольшее и наименьшее значене, то функция на этом интервале по крайней мере 1 раз принимает любые значения заключенные между наибольшим и наименьшим.
Билет 13. Задачи приводящие к понятию производной. Определение. Геометрический и физический смысл.
Р ассмотрим
движение точки от некоторого положения
М0
ассмотрим
движение точки от некоторого положения
М0
Пусть в некоторый момент времени t точка прошла пусть S и заняла положение М.,а в момент времени t +∆(t) точка была в S + ∆(S) точка М1

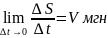 -
Мгновенная скорость;
-
Мгновенная скорость;
Скоростью
движения точки в данный момент называют
предел отношения приращения пути к
приращению времени.

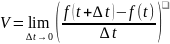 Скорость
неравномерного движения;
Скорость
неравномерного движения;
Не зависит от ∆t , зависит от t и характера функции f(t)
Пусть y=f(x) определена в некотором промежутке. Дадим прирощение∆x и ∆y. Получим
Y+∆y=f(x+∆x)
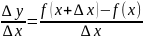 ;
;
 ; если существует то:
; если существует то:
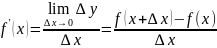
Производной функции y=f(x) называется предел отношения приращения ∆x к приращению аргумента ∆Y при ∆x0
Например:
Y=x2
Y+∆y=(x+∆x)2
∆y=(x+∆x)2 – x2
∆y=x2+2xy+∆x2-x2
∆y=2x∆x+∆x2
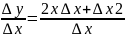 =2x+∆x
=2x+∆x
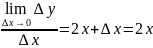
(x2)'=2x
Касательной к прямой в данной точке называется положение секущей а этой точке.

М0 М1 – секущая
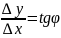
Если ∆x0 тогда М1 двигается по кривой к точке М0. Секущая М1М0 поворачивается вокруг М0 и фи меняется к предельному альфа а М1М0становится касательной к кривой вМ0
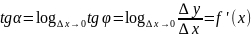
Физический смысл – мгновенная скорость при неравномерном движении. Геометрический смысл – угловой коэффициент касательной к кривой в данной точке.
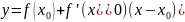 уравнениекасательной
уравнениекасательной
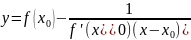 уравнение
нормаль(перпендикулярна касательной)
уравнение
нормаль(перпендикулярна касательной)
Билет 14. Связь непрерывности и дифференцируемости функции.
Если y=f(x) имеет производную в точке х0 то есть существует предел отношения то функция в точке х0называется дифференцируемой.
Если функция диф. В любой точке отрезка [a,b] или (a,b) то говорят что эта функция дифф. На данном интервале/отрезке.
Теорема. Если y=f(x) дифференцируема в некоторой точке, то она в этой точке непрерывна.
Обратная теорема не верна.
Билет 15. Общая схема получения производной.
Чтобы найти производную y=f(x) надо:
Дать приращение ∆x и вычислить y+∆y=f(x+∆x)
Найти соответствующее∆y=f(x+∆x)-f(x)
Составить отношение
Найти предел