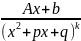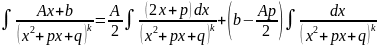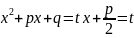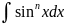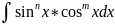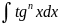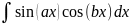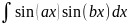Вопрос 16. Производная константы, суммы, произведения и частного.

1) сonst’=0

2)(u+v)' = u' + v'.

Докозательство.

Δ(u+v) = u (х₀+Δx)+ v(х₀+Δx) – (u(х₀)+v(х₀)) = (u(х₀+Δx)-u(х₀)) + (v(х₀+Δx)-v(х₀)) = Δu + Δv

Функции u и v дифференцируемы в точке х₀, т. е. при Δх→0

при Δх→0 т. е. (u+v)' = u'+v’

3)

Докозательство.

Y=U*V;y(x)=U(x)*V(x)

∆y=f(x+∆x)-f(x)=U(x+∆x)*V(x+∆x)-U(x)*V(x)

заменимU(x+∆x) = U(x)+∆U

V(x+∆x) = V(x)+∆V

∆y=(u(x)+∆u)*(v(x)+∆v)-u(x)*v(x)=

=u(x)*v(x)+∆u*v(X)+u(x)∆v+∆u*∆v-u(x)*v(x)=

=∆u*v(x)+u(x)*∆v+∆u∆v

  или  

Пусть     Тогда     Перейдем к пределу в каждом слагаемом. Если     то  

Если     то  

Если    то по принципу непрерывности  

  Следовательно,     что и требовалось доказать, т.е.  

4) Формулу производной частного можно получить, следуя обычной схеме вычисления производной. Но можно поступить проще. Пусть    Найдем производную функции  u  по правилу дифференцирования произведения:  Выразим из этой формулы     а вместо  h  подставим его значение     Получим: 

Окончательно   

Билет 17. Производная тригонометрических функций.

Теорема(sin(x))’=cos(x)

Докозательство.

F(x+∆x)=(Sin(x+∆x))

∆y=Sin(x+∆x) – Sin(x)=2Sin((x+∆x-x)/2)*Cos((x+∆x-x)/2)=2sin(∆x/2)*Cos(∆x/2)

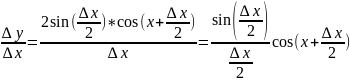
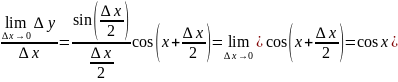ч.т.д.

Аналогично для косинуса.

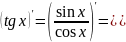
Аналогично для котангенса.

Билет18. Производная сложной функции или функции заданной неявно.

Если U=f(X) имеет в некоторых точке x производную U’_x=F(x) а функция y=F(U) имеет при соответствующем значении U производную y’_u=f’(U), то сложная функция y’=F(f(x)) в точке x имеет производную y'_x=F'_u(U)*f'_x(x)

Производная сложной функции равно произведению данной функции по промежуточному аргументу U на производную промежуточного аргумента по x .

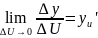
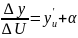По теореме о связи функции с ее пределом. - бесконечно малая величина.

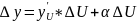
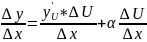
y_x'=y_u'*U_x'+0 ч.т.д.

Например:

Y=sin(x²)

Y’=cos(x²)*2x=2x*cos(x²)

Пусть переменные x и y связаны F(x,y)=0. Если функция y=f(x) на отрезке [a,b] такова, что f(x;f(x))=0 то функция y=f(x) уравнением F(x,y)=0 задана неявно.

Термины явная Функция и неявная Функция характеризует не природу функции а только способ ее задания.

Например.

X² +y²+c²=0

(x²+y²+c²)'=0'

(x²)'+(y²)'+(c²)'=0

2x+2yy'+0=0

y'=-x/y

Билет 19. Диффиренциал функции и его физический смысл. Правила нахождения.

Y=f(x);

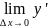
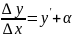- Теорема о связи функции с ее пределом

главная часть

приращения функции

Главная часть приращения функции называют дифференциалом функции(d)

Dy=y’∆x

Например

Y=x

Dx=1∆x; dx=∆x

Dy=y'dx; y'=dy/dx

Дифференциалом функции называется произведение производной функции на дифференциал аргумента.

∆y=y’∆x+α∆x, α∆x-бесконечно мала

Приращение функции отличается от своего дифференциала на величину бесконечно малую.

Точность, получаемая вычислением приращения функции не оправдывает затраченного труда. В тех случаях когда не требуется большой точности вычислений можно записать приращение функции ее дифференциалом.

AB=MB*tgα

AB=y'∆x

Dy=y'∆x

AB – приращение координаты касательной

Дифференциалом называется линейная часть приращения функции.

Dy=y’dx

Y=x²+5x

Y’=2x+5

Dy=(2x+5)dx

Правила нахождения дифференциала функции аналогичны правилам дифференцирования функции, в которых следует лишь слово производная заменить на дифференциал, так как умножив производную на дифференциал аргумента получим дифференциал функции.

Например.

Y=x²e^x

Y’=2xe^x+x²e^x=e^x(2x+x²)

Dy=e^x(2x+x²)dx

Билет 20. Инвариантность формы дифференциала. Применение дифференцирования в приближённых вычислениях.

Под инвариантностью в математике понимают сохранение вида формул при различных преобразованиях. Рассмотрим у=f(x)=> dy=f’(x) dx . Рассмотрим у=f(u) , где u=u(x)

dy=fx’(u) dx=fu’(u)*ux dx= fu’(u) du

dy=fu’(u) du

Дифференциал сложной функции имеет такой же вид,какой он имел бы,если бы промежуточная переменная была бы независимой переменной.

Иначе,форма дифференциала не зависит от того,является ли аргумент функцией независимой переменной или промежуточной переменной.

Применение дифференциала в приближенных значениях:

F(x+∆x)=f(x)≈f(x) ∆x

F(x0+∆x)≈f(x0)+f’(x0) ∆x

Пример: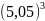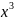

-?

У= , у’=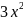

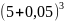, ∆x=0,05, x0=5

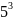F(5)= =125

F’(5)=75

= ≈125+75* 0,05=128,75

Билет 21 Производные и дифференциалы высшего порядка.

Пусть функция f(x) диф-ма на [a;b] ее производная f’(x) также функция зависящая от х. Диф-я ее мы получим также производную, которая будет являться 2-й производной по отношению к функции. производная от производной называется производной второго порядка и обозначается y”,f”(x),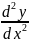

Диф-л функции y=f(x), dy=f’(x)dx в свою очередь является некоторой функцией зависящей причем от х зависит только f’(x) a dx приращение независимой переменной следовательно от х не зависит. Диф-л от диф-ла называется диф-ом второго порядка 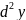Диф-ы порядка высшее первого свойством инвариантности не обладают.

Билет 22 Механический смысл второй производной. пусть s=f(t) путь пройденный телом за время t, v=ds/dt. Пусть в некоторый момент времени t v=f если движение не равномерное то за время ▲t, v изменится на величину ▲f.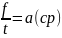

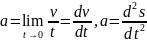, следовательно механический смысл второй производной это ускорение прямолинейного неравномерного движения.

Билет 23 Производная от функций заданных параметрически.

Пусть функция у зависит от х, но задана параметрически 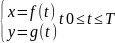пусть эти функции f и g имеют производные и пусть функция x=f(t) имеет обратную функцию t=v(x), которая так же имеет производную, тогда функция y=w(x) можно рассматривать как сложную функцию y=g(v(x)) . Y’x=Y’t*T’x=g’(t)*v’(x) на основании теоремы о диф-и обратной функции v’(x) = 1/f’(t) подставив его в формулу получим

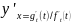
Билет 24 Теорема Ролля. если функция f(x) непрерывна на [a;b] и диф-а на (a;b)и на концах x=aи x=b функция f(x)обращается в ноль, то на (a;b) существует по крайней мере одна точка x=c(a<c<b) в которой производная равна нолю f’(c)=0 1) теорема справедлива если f(a)=f(b)≠0 2) если функция f(x) такова, что f’(x) существует не во всех точках [a;b] то теорема может быть и не верна.

Билет 25 Теорема о конечных приращениях или теорема Лагранжа. Если функция f(x) непрерывна нa [a’b]и диф-а на (a;b) то существует по крайней мере одна точка Cc(a;b) такая что f(b) – f(a)=f’(c)*(b-a)

Билет 26 Теорема о приращении двух функций или теорема Каши. Если функция f(x) и g(x) две функции непрерывных на [a;b]и диф-е на (a;b) причем g’(x)≠0 для любых Xc[a;b] то существует такая точка X=Cc(a;b) что

Билет 27 Предел отношений двух бесконечно малых величин или правило Лапиталя пусть f(x) и g(x) на [a;b] удовлетворяют условиям теоремы Каши и обращаются в 0 при x=a, тогда отношение f(x)/g(x) неопределенно при x=a но имеет вполне определенный смысл при х≠а следовательно может быть поставлен вопрос о разыскании предела этого отношения при x->a то есть вопрос о раскрытии неопределенности типа (0/0)

пусть f(x) и g(x) на [a;b] удовлетворяют условиям теоремы Каши и обращаются в 0 при x=а тогда если существует предел 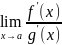то существует 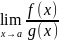причем эти пределы равны. 1) если в условиях теоремы А=∞ то теорема справедлива и в этом случае 2) если х->∞ то теорема верна и в этом случае 3) теорема верна и тогда когда f(x) и g(x) неопределенны при x=a но

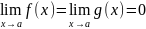. 4) если обе производные равны нолю и удовлетворяют тем же условиям что и сами функции то

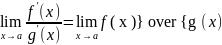
Билет 28 Предел отношений двух бесконечно больших величин. Пусть f(x) и g(x) непрерывны и диф-ы при всех х≠а в окрестности точки а причем g’(x)=0 и пусть 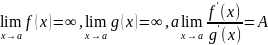то предел

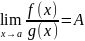
Билет 29 Возрастание и убывание функций. функция y=f(x) называется возрастающей на (a;b) если для любых х1,х2с(a;b) таких что х1<х2 следовательно f(x1)<f(x2) функция y=f(x) называется убывающей на (a;b) если для любых х1,х2с(a;b) таких что х1<х2 следовательно f(x1)>f(x2) Если функция f(x) имеющая производную на [a;b] возрастает на этом отрезке то ее производная на этом отрезке больше или равна нолю. Если функция непрерывна на [a;b] и диф-а (a;b) причем f’(x)>0 на этом интервале, то функция f(x) возрастает на [a;b] Док-во: 1) пусть f(x) возрастает на [a;b] дадим х приращение х и рассмотрим 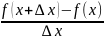так как функция возрастает то при x>0 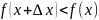при x<0 2) пусть f’(x)>0 для любых xc(a;b) рассмотрим x1,x2c(c,b) таких что x1<x2 по теореме Лагранжа f(x2)-f(x1)=f’(c)*(x2-x1) x1<c<x2 по условию теоремы f’(с)>0 тогда f(x2)-f(x1)>0, f(x2)>f(x1) следовательно f(x) возрастает [a;b].

Билет 30 Максимум и минимум. Определение : Функция имеет максимум в х1, если F(x+∆x)<f(х1) для любых ∆х достаточно малых по абсолютной величине.

Функция имеет минимум в х2, если F(x+∆x)>f(х2) для любых ∆х достаточно малых по абсолютной величине.

Особенности понятия:

1. Функция f(x) может иметь максимум или минимум только внутри отрезка.

2. Максимум и минимум не равны наибольшему и наименьшему значениям функции

Понятия максимум и минимум имеют локальный характер

максимум и минимум функции называют – экстремумы функции

Теорема: Необходимые условия существования экстремума:

Если дифференциальная функция имеет в х=х1 экстремум,то производная в этой точке равна нулю.

Доказательство: Пусть в х1-максимум,то F(x+∆x)<f(х1), т.е.

F(x1+∆x)-f(x1)<0

[F(x1+∆x)-f(x1)]/ ∆x<0, при ∆х>0

[F(x1+∆x)-f(x1)]/ ∆x>0, при ∆х<0

F’(x)=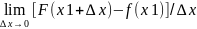

Если 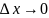, ∆х<0, то f’(x1)>=0

Если , ∆х>0, то f’(x1)<=0 , следовательно f’(x1)=0. Теорема доказана.

Пусть в х1-минимум. Доказать дома

Касательная проведенная к кривой точки экстремума параллельно к оси х.

Точки,в которых производная =0 или не существует называют критическими точками первого рода

Теорема Достаточное условие существования экстремума:

Пусть функция непрерывна в некотором интервале содержащим критическую точку х1 и дифференцируема во всех точках этого интервала,кроме быть может самой точки х1.

Если при переходе слева направо через х,производная меняет знак с + на - ,то в х1- максимум, если наоборот- минимум.

Доказательство. Пусть  при  и  при .

По теореме Лагранжа , где .Тогда если , то ; поэтому  и , следовательно, , или . Если же , то ; поэтому  и , следовательно,  или .

Таким образом доказано, что  в любых точках вблизи , т.е.  – точка максимума функции .

Доказательство теоремы для точки минимума проводится аналогично. Теорема доказана.

Билет 31 .Исследование функции на экстремум с помощью второй производной.

Пусть в точке x1 первая производная равна нулю f ’1(x1)=0 и вторая производная f ’’2(x) cсуществует и непрерывна в некоторой окрестности точки x1,тогда справедлива следующая теорема.

Теорема. Пусть f ‘(x1)=0, тогда при x=x1, функция в точке x1 имеет max f ‘’(x1)<0

min f ‘’(x2)>0

Доказательство.

А)Пусть f ‘(x1)=0 и f ‘’(x1) <0 , т.к.f’’(x1) по условию теоремы непрерывно в некоторой окрестности:

Точки x1, то существует маленький отрезок окружности

Точки x1,такой что во всех точках отрезка

f ‘’(x1)<0

f ‘’(x)= (f ‘(x))’<0 f ‘(x) убывает, но f ‘(x1)=0, значит что ,

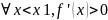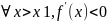
т.е. при переходе через точку x1 f ‘(x) сменила знак с +на -, значит в точке x1 функция f(x) имеет max.

Б)Пусть f ‘(x2)=0 и f ‘’(x2)>0, т.к. f’’(x2) по условию теоремы непрерывно в некоторой окрестности:

Точки x2, то существует маленький отрезок окружности

Точки x2,такой что во всех точках отрезка

f ‘’(x2)>0

f ‘’(x)= (f ‘(x))’>0 f ‘(x) возрастает, но f ‘(x2)=0, значит что ,

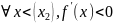
т.е. при переходе через точку x2 f ‘(x) сменила знак с -на +, значит в точке x2 функция f(x) имеет min.

Билет 32.Наибольшее и наименьшее значение функции на отрезке.

1.найти все критические точки на этом отрезке(принадлежащем ему)

2.Вычислить значение функции в этих точках и на концах отрезка

3. выбрать наибольшее и наименьшее значение.

П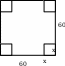 ример. Сделать коробку без крышки, 60*60см из квадратного листа картона, наибольшего объёма.

V=S0*h=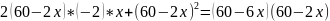

V’=0

60-2x=0, x1=30

60-6x=0, x2=10

V(10)=1600

V(0)=0

V(30)=0

Билет 33.Выпуклости и вогнутости кривой. Точки перегиба.

Кривая называется выпуклой на интервале, если все её точки лежат ниже любой касательной на этом интервале.

К ривая называется вогнутой на интервале, если все её точки лежат выше любой касательной на этом интервале.

Теорема1. Если во всех точках (а:b) f ‘’(x)<0(отриц.), то кривая 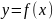выпуклая на этом интервале.

Доказательство.

X0 €(a;b).Теорема будет доказана, если мы установим, что все точки кривой лежат под касательной, т.е. ординаты точек кривой, меньше ординаты точек касания.

(1)

(2)

Вычтем из (1) (2)

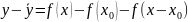
применим т. Лагранже

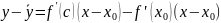, где с лежит между x и

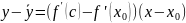
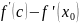применим т.Лагранже

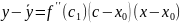3,где С1 лежит между

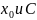
1.Случай. x> 2.Случай. x<

<C1<C<x <C1<C<

C- >0 , x- >0 C- <0 , x- <0

f’’(C1)<0 f’’(C1)<0

Таким образом точки кривой лежат под касательной, ч.т.д.

Теорема2.Если в любых точках (b;c), f’’(x)>0, то кривая на этом интервале вогнутая.

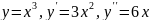
y’’>0

Точки перегиба - точка, отделяющая выпуклую часть кривой от вогнутой.Очевидно, что в точках перегиба, касательные пересекают прямую, т.к. с одной стороны кривая должна лежать под касательной, а с другой над касательной.

Установим достаточное условие существования точек перегиба.

Теорема. Пусть кривая определяется уравнением , если f’’(a)=0 или не существует и при переходе через точку x=a f’’(x) меняет знак, тогда точка с координатами (a;f(a)), является точка перегиба.

Доказательство.

1часть: Пусть f’’(x)<0 и кривая выпуклая

f’’(x)>0 и кривая вогнутая.

2.часть. Пусть f’’(x)>0 и кривая вогнутая

f’’(x)<0 и кривая выпуклая; следовательно x точка перегиба.

Пример.

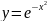кривая Гаусса

+ - +

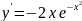
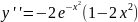
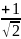
Y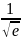пер( )= , Yпер( )=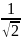

План нахождения точек перегиба и интервал выпуклости и вогнутости:

1.находим критические точки второго рода, т.е. точки в которых вторая производная равна нулю или не существует.

2.разбиваем этими точками D(y) на интервале

3. определяем знак второй производной на каждом из полученных интервалов

5.определяем точки перегиба.

Билет 35. Асимптоты кривой

Часто приходится исследовать форму кривой при неограниченном возрастании по абсолютной величине, абсциссы или ординаты точки кривой при этом важен случай, когда кривая при удалении её переменных точек в бесконечность, неограниченно приближалась к некоторой прямой.

О пределение. Прямая называется асимптотой кривой, если расстояние δ от переменной точки кривой М до этой прямой стремящейся к 0, при м стремящейся к бесконечности.

δ

Асимптоты делятся на вертикальные и горизонтальные.

1.Вертикальные асимптоты, ес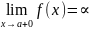ли

или

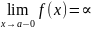
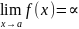,то прямая x=a является вертикальной асимптотой,a=0.

Для опускания вертикальных асимптот, нужно найти такие значения x=a, при приближении к которой y стремится к бесконечности, это точки разрыва функции и точки лежащие на границах области определения функции.

2.Наклонные асимптоты.

П усть кривая , имеет наклонную асимптоту, y=kx+b, найдём k и b.

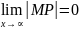
Рассмотрим 𝞓MNP:

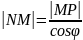
Т.к. φ=const, тогда

*

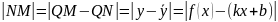
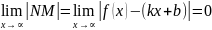Следовательно

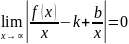
Т.к.b=const, ,

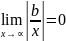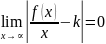
k= , подставив в *, b=

Билет 35.Полное исследование функции.

I.Исследование функции по виду.

1.найти D(y)

2.чётность, нечётность. Периодичность.

3.нули функции

4.промежутки знака постоянства функции

II.Исследование с помощью пределов.

1.исследовать на непрерывность в точке разрыва.

2.односторонние пределы в точках разрыва и на границах D(y).

3.вертикальные асимптоты.

4.наклонные асимптоты.

III.Исследование с помощью первой производной.

1.найти первую производную

2. критические точки 1ого рода.

3.промежутки монотонности.

4.точки экстремума.

IV. Исследовать с помощью второй производной.

1.найти вторую производную.

2. критические точки второго рода.

3.промежутки выпуклости и вогнутости.

4. точки перегиба.

V. Построить график.

Билет 36.Первообразная и неопределённый интеграл

Основная задача диф.счисления, отыскание производной данной функции.

Основная задача интегрир.счисления, отыскание функции по её данной производной.

Определение.

1.Функция F(x) называется первообразной от функцииf(x) на [a;b], если во всех точках этого отрезка,F’(x)=f(x).

Легко заметить, что если для функции существует первообразная, то она не единственная.

,

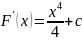,где с постоянная.

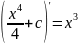
C другой стороны докажем что функция 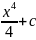исчерпывает все первообразные от функции f(x) на [a;b], то разность между ними равна const числу.

Доказательство.

Из определения1 следует

F1’(x)=f(x)

F2’(x)=f(x),(1) при всех x€[a;b].

Обозначим разность между

F1’(x)- F2’(x)=φ(x) (2)

Тогда из первого равенства следует

F1’(x)- F2’(x)=0

или φ’(x)= F1’(x)- F2’(x)=0, для всех x€[a;b].

φ(x)=const.

Действ. Применив т.Лагранже, функция φ(x) на этом отрезке непрерывна и диф. для всех x€[a;b].

φ(x)- φ(a)=(x-a)φ’(ξ)

a< ξ<x, φ’(ξ)=0, φ(x)=φ(a)

F1’(x)- F2’(x)=const.ч.т.д.

Следствие.

Если функция F(x) какая нибудь первообразная от функции f(x), то любая другая первообразная имеет вид F(x)+c.

Определение2.Если функция F(x), является первообразной от функции f(x),то выражение F(x)+c называется неопределённым интегралом от функции f(x) и обозначается таким образом.

интеграл, = F(x)+c, если F’(x)=f(x)

f(x)-подынтегральная функция

f(x)dx- подынтегральное выражение

∫-знак интеграла.

Таким образом. Неопределённый интеграл это семейство функций.

Теорема. Если функция f(x) непрерывна на [a;b], то для неё существует первообразная, а значит и неопределённый интеграл.

Нахождение первообразной для данной функции называется интегрированием данной функции.

Билет 37.Свойства неопределённого интеграла

1.производная от неопределённого интеграла равна подынтегральной функции, т.е. если F’(x)=f(x), (

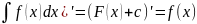
2.дифференциал

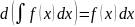
3. =F(x)+c

4.f[ f1(x)+f2(x)]dx=∫f1(x)dx+∫f2(x)dx

5.∫af(x)dx=a∫f(x)dx, a=const.

Доказывается, дифференцированием обеих частей равенства.

Справедливость всех формул доказывается диф.,т.е. показывают, что производная от правой части, равна подынтегральной функции.Кроме того при интегрировании некоторой функции бывает полезным следующие правила:

1.Если ∫f(x)dx=F(x)+c, то∫f(ax)dx= 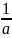F(ax)+c

2.Если ∫f(x)dx=F(x)+c, то ∫f(x+b)dx= F(x+b)+c

3. Если ∫f(x)dx=F(x)+c, то ∫f(ax+b)dx= F(ax+b)+c

Билет 38.Интегрирование методом замены переменной или способ подстановки.

Пусть требуется найти ∫f(x)dx, причём непосредственно подобрать F(x) мы не можем, но она существует, сделаем замену переменной подынтегрального выражения, положив x=φ(t) (1), где φ(t) непрерывная функция с непрерывной производной, имеющей обратную функцию dx= φ’(t)dt (2)

Для этого продиф. Обе части равенства по x:

1. (∫f(x)dx)’=f(x)

2. (∫f(φ(t))φ’(t)dt)’=(∫f(φ(t)φ’(t)dt)’ 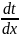= =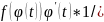f(φ(t))=f(x)

Равенство 2 доказано.

Замечание, иногда целесообразно подбирать замену переменных в виде t=φ(x), тогда φ’(x)dx=dt

Пример :

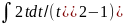= = 2∫dt/( 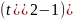=2*(1/2)ln 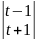+c.

Билет 39.Интегралы от некоторых функций содержащих квадратный трёхчлен.

,

)=

1. = = = ( + = +

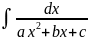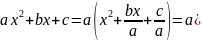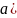
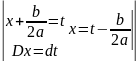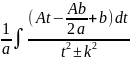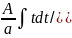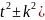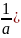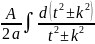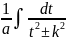
Билет 40. Интегрирование по частям.

Пусть u и v –две дифференцированных функции зависящие от х.

D(uv)=u dv+v du

∫d(uv)=∫u dv+∫v du

Uv= ∫u dv+ ∫v du

∫u dv= uv-

∫v du

Пример:

∫хcosx dx= 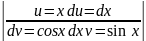=x sinx-∫sinx dx= x sinx+ cosx+c

Билет 41. Простейшие рациональные дроби и их интегрирование

Существуют такие классы функций, интегрирование от которых, выражается через элементарные функции. Простейший из таких классов – рациональный. Всякую рациональную функцию R(x) можно представить в виде рациональной дроби:

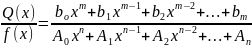
Если степень числителя меньше степени знаменателя – дробь правильная, если больше или равна – неправильная.

Неправильная дробь	Целая часть	Правильная дробь

Т.к. интегрирование многочленов не представляет трудностей, то выясним как интегрировать правильные дроби.

Простейшими дробями называются правильные рациональные дроби следующих типов:

	= = +…
	Интегрирование по частям

Билет 42. Интегрирование рациональных дробей

Покажем что любую правильную дробь можно разложить на простейшую. Пусть предположим что коэффициенты входящих в нее многочленов - действительных чисел и эта дробь несократима, т.е. числитель и знаменатель не имеют общих корней.

Пусть x=a корень знаменателя кратности k, т.е. f(x)=(x-a)^k*f₁(x), где f1(x)≠0, тогда

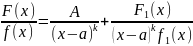, A≠0, A – const,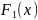 - многочлен, степень которого ниже степени знаменателя.

Пример №1:

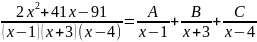
2x²+41x-91=A(x+3)(x-4)+B(x-1)(x-4)+C(x-1)(x+3)

2x²+41x-91= A(x²-x-12)+B(x²-5x+4)+C(x²+2x-3)

2x²+41x-91= A x²- Ax- A*12+ Bx²- B*5x+4* B+ Cx²+ C*2x - 3* C

2x²+41x-91=(A+B+C)*x²+(-A-5B+2C)x+(-12A+4B-3C)

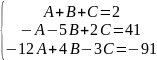решаем систему методом Гаусса/Крамера/и т.п.

Частный случай:

2x²+41x-91=A(x+3)(x-4)+B(x-1)(x-4)+C(x-1)(x+3)

x=1:

2*1+41*1-91= A(1+3)(1-4)+B(1-1)(1-4)+C(1-1)(1+3) → -48=-12А → А=4

x=-3

2*9+41*(-3)-91=A(-3+3)( -3-4)+B(-3-1)( -3-4)+C(-3-1)( -3+3) → -196=28B → B=-7

x=4

2*16+41*4-91=A(4+3)( 4-4)+B(4-1)( 4-4)+C(4-1)( 4+3) → 105=21C → C=5

Интегрируем:

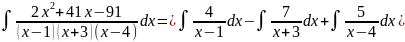
Пример №2:

x² - 3x+2=A(x+1)²+B(x)(x+1)+C(x) Далее аналогично предыдущему.

Пример №3:

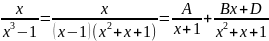
x=A(x²+x+1) +(Bx+D)(x-1) Далее аналогично предыдущему.

Пример №4:

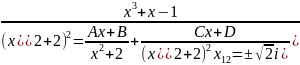
x³+x-1=(Ax+b)(x²+2)+Cx+D

x³+x-1=Ax³+Bx²+2Ax+2B+Cx+D

x³+x-1=Ax³+Bx²+(2A+C)x+(2B +D)

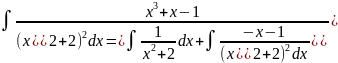
Пример №5:

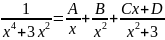
1=Ax(x²+3)+B(x²+3)+(Cx+D)*x²

1=Ax³+3Ax+Bx²+3B+C x³+Dx²

1=(A+C)x³+(B+D)x²+3Ax+3B

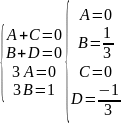
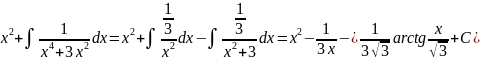
Билет 43. Интегрирование некоторых классов тригонометрических функций

1класс:	m и n целые положительные числа
2 класс:
3 класс:
4 класс:

1 правило

Интеграл от четных степеней синусов или косинусов, можно найти путем понижения степени:

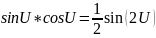
2 правило

Интеграл от нечетных синусов или косинусов, находится путем отделения от него одного множителя и заменой ко-функцией для новой переменной

3 правило

Интегралы класса 2 можно найти по 1 правилу, если обе степени (m и n) – четные, и по 2 правилу если хоть одна из этих степеней нечетная.

4 правило

Интегралы 3-его класса можно вычислить с помощью замены: tg(x)=t или ctg(x)=t

5 правило

Интегралы 4-ого типа можно вычислить с помощью формул:

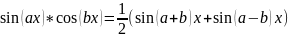
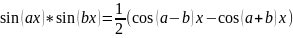
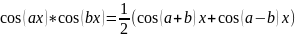
Пример №1:

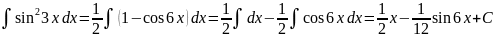
Пример №2:

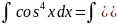
Пример №3:

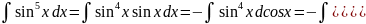
Пример №4:

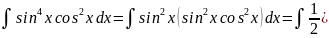
Пример №5:

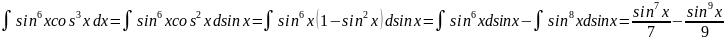
Пример №6:

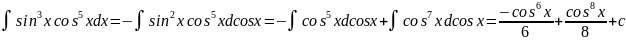
Пример №7:

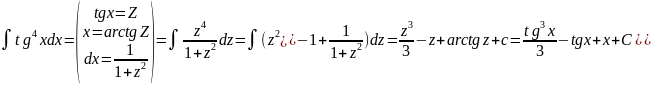
Пример №8:

Билет 44. Универсальная тригонометрическая подстановка

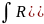
Выводы:

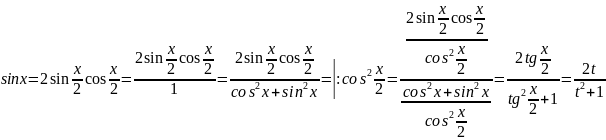
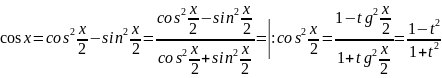
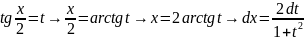
Пример №1:

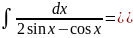
Билет 45. Интегрирование иррациональных функций

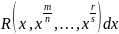1. т.е. R – иррациональная функция от иррациональных аргументов.

Пусть k – общий знаменатель для 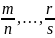, тогда делается замена x=t^k, при такой подстановке каждая дробная степень x, выразится через дробную степень t, т.е. подынтегральная функция станет рациональной функцией зависящей от t.

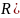2. . тут так же общий знаменатель k. Делаем замену

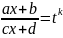
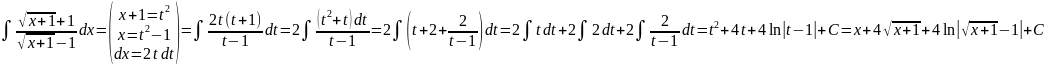
Билет 46. Определенный интеграл. Теорема о существовании

О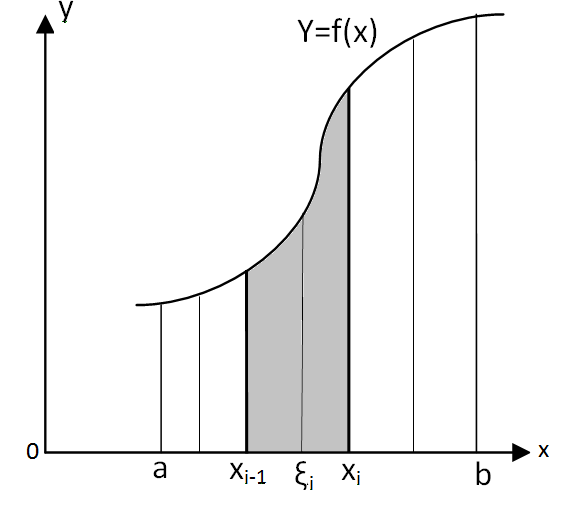 пределение: Фигура ограниченная снизу осью x, сверху кривой y=f(x) и с боков кривыми x=a и x=b, называется криволинейной трапецией.

1. a=x₀; x₁; x₂;…;x_i;x_i+1;…x_n=b

2. ∆x_i=x_i-x_i-1 (i=1,…,n)

3. ξiϵ(x_i-1;x_i)

4. ∆Si≈∆xi*f(ξi)

5. 

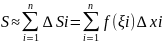
y=f(x)на отрезке [a,b]. Разобьем отрезок [a,b] на n частей точками (пунтк 1). Длину каждого участка разбиения обозначим как ∆xi (пункт 2). На каждом из участков разбиения выбираем точку ξi (пункт 3). Для каждого i составим произведение (пункт 4) b получаем интегральную сумму (пункт 5).

Теперь переходим к пределу:

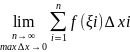
Если этот предел не зависит от способа разбиения отрезка [a,b] на части и выбора точки ξ на каждом из участков, то его называют определенным интеграломи обозначают:

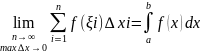(*) , где

a – нижний предел интегрирования

b – верхний предел интегрирования

x – переменная интегрирования

[a,b] – отрезок интегрирования

Если для функции предел (*) существует, то функция называется интегрируемой на отрезке [a,b].

Теорема существования:

Если функция f(x) непрерывна на отрезке [a,b], то она интегрируема на этом отрезке.

Билет 47. Основные свойства определенных интегралов.

1. Определенный интеграл не зависит от обозначение переменной интегрирования

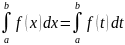
Док-во: величина определенного интеграла есть число равное площади криволинейное трапеции которая не зависит от названия оси абсцисс.

2. При перестановке границ интегрирования между собой, знак интегрирования меняется на противоположный

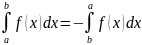
3. Интеграл от а до а, равен 0

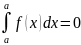
Док-во: при b→a, S=0

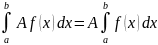4. , где A=const

Док-во:

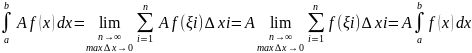
5. Интеграл суммы, равен сумме интегралов

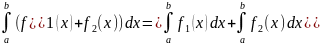
Док-во:

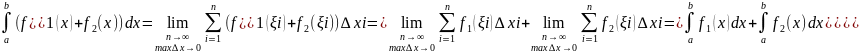
Аналогичные теоремы распростроняются на любое конечное число слагаемых

6. Если на [a,b] (где a<b), f(x)≤φ(x) то

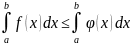
Док-во:

Рассмотрим разность

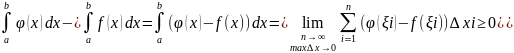
(т.к. )

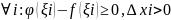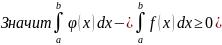
7. Если m и M наименьшее и наибольшее значение функции на отрезке [a,b] и a≤b то

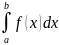m(b-a) ≤ ≤ M(b-a)

Док-во:

По условию m≤f(x) ≤M , 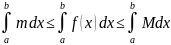, значит m(b-a) ≤ ≤M(b-a)

8. Теорема о среднем

Функция f(x)непрерывна на [a,b] то на этом отрезке найдется такая точка ξ что справедливо равенство:

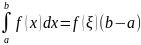
Док-во:

Пусть M и m наибольшее и наименьшее значения f(x) на промежутке [a, b]. Составим для f(x) какую-нибудь интегральную сумму

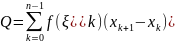
Так как при всех k будет m ≤ f(ξk) ≤ M, а xk+1 > xk, то m(xk+1 - xk) ≤ M(xk+1 - xk). Складывая такие неравенства и замечая, что

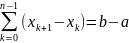
получим:

m(b - a) ≤ Q ≤ M(b - a).

Переходя в этом неравенстве к пределу при λ → 0, приходим после деления на b - a к новому неравенству

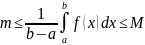
Таким образом, частное

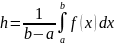
есть число, лежащее между наибольшим и наименьшим значениями непрерывной функции. Как известно, тогда и само это число должно являться одним из значений той же функции. Поэтому в [a, b] обязательно существует такая точка ξ, что h = f(ξ), а это равносильно равенству

9. Для любых a,b,c справедливо

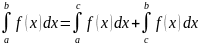
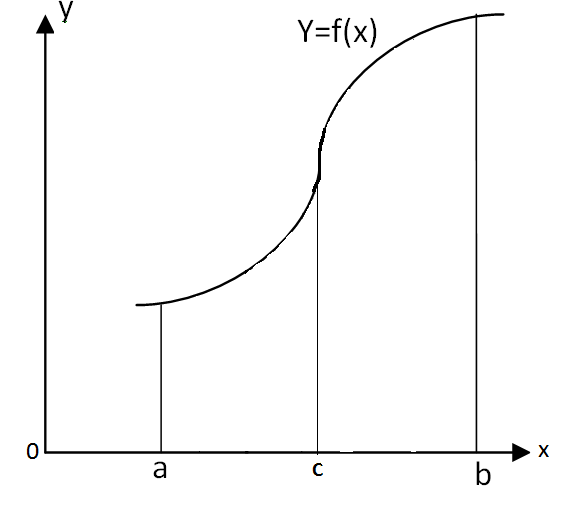
Только если все 3 интеграла существуют

Док-во:

Пусть a<c<b. Составим интегральную сумму для функции f(x) на [a,b]

Т.к. Предел интегрирования суммы не зависит от способа разбиения [a,b] на части, то будем [a,b] разбивать так, что с :

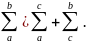
Значит при a<c<b

Билет 48. Интеграл с переменным верхним пределом

Пусть в определенном интеграле нижний предел а, зафиксирован и верхний предел b меняется, тогда будет меняться и значение Ф(х)= .

Пусть f(x) - непрерывная функция, заданная на промежутке [a, b]. Тогда она будет непрерывной и на всяком частичном промежутке [a, x], и можем рассмотреть интеграл

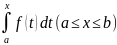
являющийся функцией аргумента x (как указывалось раньше, обозначение переменной интегрирования не существенно, чтобы не путать эту переменную с пределом интегрирования, обозначаем ее через t).

Теорема. Производная определенного интеграла от непрерывной функции, рассматриваемого как функция его верхнего предела, существует и равна значению подинтегральной функции в точке дифференцирования.

В виде формулы высказанное утверждение выглядит так:

Если же положить

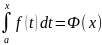
т о формулированную теорему можно будет записать равенством

Ф’(x)=f(x)

Дадим х приращение ∆х тогда

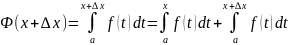
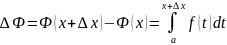
К последнему применяем теорему о среднем

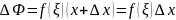
ξ – расположена между х и ∆х+х

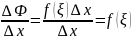
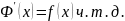
Билет 49. Формула Ньютона-Лейбница

Если функция F(x) есть первообразная от непрерывной функции f(x) то

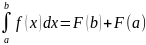
Док-во:

Пусть F(x) первообразная для f(x), тогда из 47 билета (см. выше) 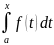так же является первообразной для f(x). Тогда (2)

Найдем 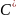при котором (2) станет тождественным. Положим в этом равенстве х=а

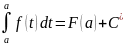
Значит

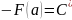
(2) →

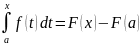
В полученном равенстве, положим х=b

Билет 50.Замена переменной в определенном интеграле

Пусть дан , где f(x)-непрерывная на [a,b] функция, выделим переменную t по формуле x= (t),если , 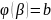. (t) и ’(t) непрерывна на [a,b]. f( (t)) определенна и непрерывна на ,

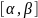То 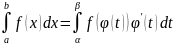(1)

Доказательство:

Если F(x) первообразная для f(x),то 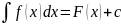(2), то (3).

Справедливость (3) формулы легко проверить продеференциировав по t.

(2) =>

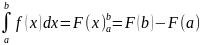
(3)=>

Не возвращаясь к старой переменной

Ч.т.д.

Билет 51. Интегрирование определенного интеграла по частям.

Пусть u и v функции зависящие от x,тогда (u*v)’=u’v+uv’.

Тогда:

Пример:

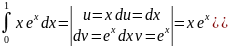
Билет 52. Несобственные интегралы с бесконечным пределом интегрирования.

Пусть f(x) определенна и непрерывна на [a;+ ).

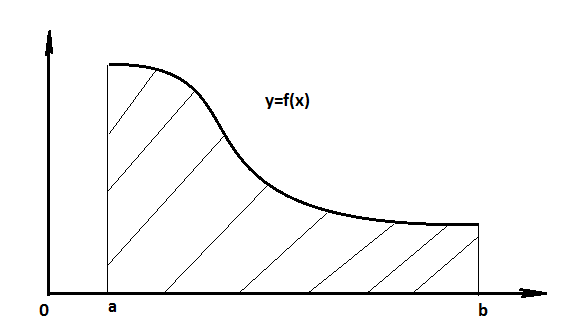
Рассмотрим , интеграл имеет смысл при b>a,если b изменяется, то изменяется и весь интеграл. Тоесть интеграл есть непрерывная функция зависящая от b.

Рассмотрим поведение интеграла при b стремящемуся в бесконечность.

Определение:

Если существует 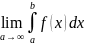,то его называют несобственным интегралом от f(x) на [a;+ ).

Если 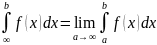то в этом случаи интеграл сходится.

Если нет конечного предела, то интеграл не существует.

Интеграл расходится ,если хотя бы один предел не существует.

Пример:

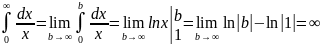
Во многих случаях достаточно установить сходится интеграл или расходится и оценить его значение, для полезны следующие теоремы:

1)Если x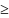 a выполняется 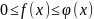и если 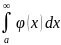cходится ,то 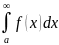тоже сходится, причем выполняется

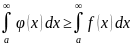
2) Если x a выполняется и если расходится ,то тоже расходится.

Билет 53.Интегралы от разрывных функций

Пусть функция определенна и непрерывна на [a,c) и при x=c функция любо неопределенна либо терпит разрыв. В этом случаи говорить о интеграле как определенном нельзя. Т.к. предел может не существовать.

Если существует-сходится. Не существует-расходится.

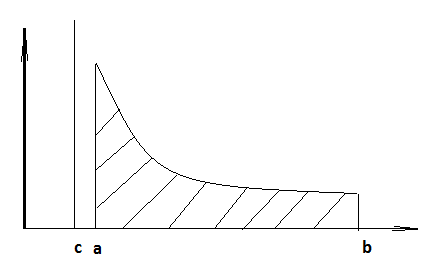
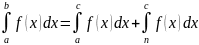
Билет 54. Геометрические приложения определенного интеграла(площади плоских фигур в прямоугольных координатах).

a

b

S=

Н аходится через предел.

a

b

S=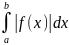

a

b

S=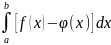

Билет 55. Площадь криволинейного сектора в полярных координатах

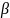
Для вычисления площади криволинейного сектора разобьем отрезок [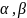 ] вектором произвольным образом.

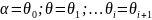
1)Разобьем отрезок

2)Выберем производным образом точку

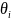
3)Посчитаем значение функции в этой точке

4)Предположим, что на каждом из отрезков значение постоянно и равно значению выбранной точки.

5)Получаем N круговых секторов.

6)

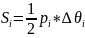
S=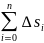

7)Перейдем к пределу 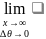и максимально получим значение площади.

Билет 56.Длина дуги в прямоугольных координатах, полярных и функции, заданной параметрически.

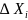
Y=f(x)

A

B

a

b

Билет 60.Вычисление работы с помощью опред. интеграла.

F-сила, М- материальная точка,движущаяся от а до б.

1)F=const, A=F(b-a)

2)F=F(S). Разобъем [a,b] на n частей произвольным образом,получим ∆S1….∆Sn.

£ [xi,x(i+1)]. Считаем F в этой точке и предполагаем ,что на каждом ∆Si, F-постоянно равно F в выбранной точке, тогда A=

Координаты центра тяжести.

Пусть на плоскости дана система материальных точек P1(x1,y1),….Pn(xn,yn)

И m1,m2….mn

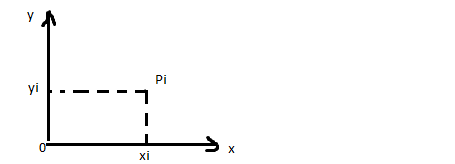
Xi*mi-статистический момент массы относительно Оу.

Yi*mi-относительно Ох

Координаты центра тяжести:

Xi=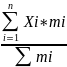

yi=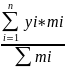

Билет 61. Центр тяжести плоской линии.

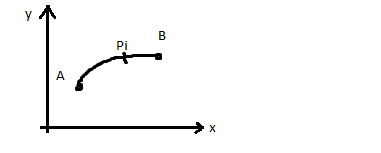
Пусть дана дуга (А,В) уравнением у=f(х), х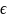 [a,b] и пусть эта дуга-материальная линия; линейная плотность-ɣ=const. Разобъем дугу (А,В) на n частей произвольным образом и получим ∆S1, ∆S2,… ∆Sn. ∆m= ɣ∆Si. Возьмем на каждом из участков £i [xi,x(i-1)], f(£i), Pi= (£I, f(£i)) предположим,что ∆mi расположена в Pi, тогда Х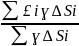i≈ , yi≈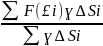 . Перейдем к интегралу в каждом случае, получим Х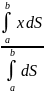i= , Yi=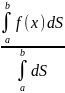 , где dS=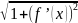

Билет 62. Центр тяжести плоской фигуры.

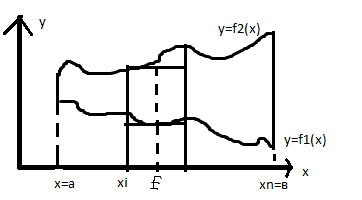
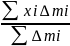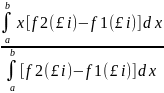Плоская фигура,ограниченная [а,в], поверхностная плотность ɣ=const. Выберем £i, так что £i= (х(i+1)+ хi)/2, а , f(£i)= ( f2(£i)+ f1(£i))/2. ∆mi= ɣ[f2(£i)-f1(£i)] ∆хi, т.к. хi= , y= , при подстановке ∆mi получим х= , у=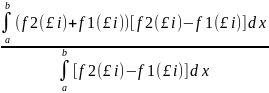
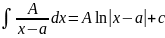
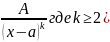
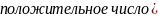
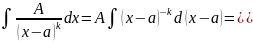
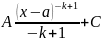
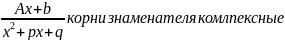
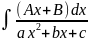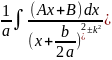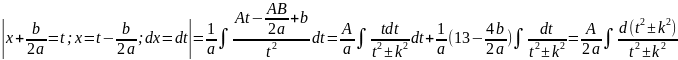