Билет 1

А)Решение системы линейных уравнений по формулам Крамера

Теорема Крамера. Система n линейных уравнений с n неизвестными имеет единственное решение, если определитель системы не равен 0, и это решение находится по формуле Крамера:

Б)Исследование функции на возрастание, убывание

Билет 2

А)Определители. Их свойства. Решение линейных уравнений методом Гаусса

Простейший определитель состоит из 4 чисел, называемых элементами и расположенных в виде 2-х строк и 2-х столбцов. О таком определителе говорят, что он 2-го порядка. Например, таков определитель

Определитель 3-го порядка состоит из 9 элементов, расположенных в виде 3-х строк и 3-х столбцов. В общем случае определитель n-го порядка состоит из n2 элементов, и обычно его записывают как

Свойства определителя.

Среди наиболее важных свойств определителя назовем следующие.

(i) Если все элементы любой строки (или любого столбца) равны нулю, то и значение определителя равно нулю:

(ii) Если элементы двух строк (или двух столбцов) равны или пропорциональны, то значение определителя равно нулю:

(iii) Значение определителя не изменится, если все его строки и столбцы поменять местами, т.е. записать первую строку в виде первого столбца, вторую строку – в виде второго столбца и т.д. (такая операция называется транспонированием). Например,

(iv) Значение определителя не изменится, если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на произвольный множитель. В следующем примере элементы второй строки умножаются на –2 и прибавляются к элементам первой строки:

(v) Если поменять местами две строки (или два столбца), то определитель изменит знак:

(vi) Если все элементы одной строки (или одного столбца) содержат общий множитель, то этот множитель можно вынести за знак определителя:

метод гаусса Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменны

Б)Исследование функции на выпуклость, вогнутость

Нахождение интервалов выпуклости и вогнутости. Это делается с помощью исследования знака второй производной f (x). Найти точки перегиба на стыках интервалов выпуклости и вогнутости. Вычислить значение функции в точках перегиба. Если функция имеет другие точки непрерывности (кроме точек перегиба), в которых вторая производная равна 0 либо не существует, то в этих точках также полезно вычислить значение функции. Найдя f (x) , мы решаем неравенство f (x) 0. На каждом из интервалов решения функция будет выпуклой вниз. Решая обратное неравенство f (x) 0, мы находим интервалы, на которых функция выпукла вверх (то есть вогнута). Определяем точки перегиба как те точки, в которых функция меняет направление выпуклости (и непрерывна).

Билет 3

А)Матрица. Действия с ними

Матрицей размера n * x называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Операция сложения матриц вводится только для матриц одинакового размера, т. е. дляматриц, у которых число строк и столбцов соответственно равно. Суммой матриц А и В, называется матрица С, элементы которой равны сумме соответствующих элементов.

Аналогично определяется разность матриц.

Умножение матрицы на число:

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число. Произведением матрицы А на число k называется матрица В, такая что bij = k × aij.

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы Аm×n на матрицу Вn×p, называется матрица Сm×p такая, что сik = ai1 × b1k + ai2 × b2k + ... + ain × bnk, т. е. находиться сумма произведений элементов i - ой строки матрицы А на соответствующие элементы j - ого столбца матрицы В. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А × Е = Е × А = А, где А квадратная матрица, Е - единичная матрица того же размера.

Б)Дифференциал. Применение дифференциала в приближенных вычислениях

Билет 4

А)Вектор. Действия с ними. (длина, компланарность , коллениарность)

Понятие вектора

Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Направление вектора (от начала к концу) на рисунках отмечается стрелкой. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления. Нулевой вектор обозначается символом 

Длиной ненулевого вектора   называется длина отрезка AB. Длина вектора  (вектора  ) обозначается так:    . Длина нулевого вектора считается равной нулю:  . Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой ил на параллельных прямых. Если два ненулевых вектора   и   коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы   и   называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы   и   называются противоположно направленными. Нулевой вектор принято считать сонаправленным с любим вектором.

Векторы называются компланарными, если имеются равные им вектора, параллельные одной плоскости.

Б)Первый замечательный предел (вывод)

Первый замечательный предел. Так называют легко выводимую в курсе математического анализа формулу

,

где аргумент х измеряется в радианах

Из первого замечательного предела следует эквивалентность при х →0 следующих бесконечно малых величин: ах, sinax; tgax; arcsinax; arctgax. Это означает, что предел отношения двух любых из этих функций при х →0 равен 1.

Следствия

Билет 5

А)Скалярное произведение векторов

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

Скалярное произведение векторов  ,   обозначается символом   (порядок записи сомножителей безразличен, то есть  ).

Если угол между векторами  ,   обозначить через  , то их скалярное произведение можно выразить формулой

 (1)

Скалярное произведение векторов  ,   можно выразить также формулой

, или  .

Б)Предел функции. Теоремы пределов (свойства)

Предел функции — одно из основных понятий математического анализа. Функция f(x) имеет предел L в точке x₀, если для всех значений x, достаточно близких к x₀, значение f(x) близко к L.

Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине).

Обозначение предела функции

Предел функции обозначается как

или через символ предела функции:

Если при прочтении данного материала у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме, также на форуме Вам помогут решить задачи по математике,геометрии, химии, теории вероятности и многим другим предметам.

Свойства пределов функции

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

Аналогично предел разности двух функций равен разности пределов этих функций.

Расширенное свойство предела суммы:

Предел суммы нескольких функций равен сумме пределов этих функций:

Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

Расширенное свойство предела произведения

Предел произведения нескольких функций равен произведению пределов этих функций:

5) Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

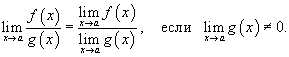
Билет 6

А)Векторное произв. Векторным произведением векторов   и   называется вектор  , который определяется следующими условиями:

1) Его модуль равен   где   - угол между векторами   и  .

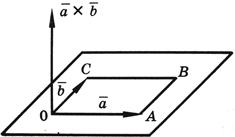
2) Вектор   перпендикулярен к плоскости, определяемой перемножаемыми векторами   и  .

3) Вектор   направлен так, что наблюдателю, смотрящему с его конца на перемножаемые векторы   и  , кажется, что для кратчайшего совмещения первого сомножителя со вторым первый сомножитель нужно вращать против часовой стрелки (см. рисунок).

Векторное произведение векторов   и   обозначается символом  :

     (25)

или

     (26)

Б)Бесконечно малые и бесконечно большие

Бесконечно малые.

Переменная   называется бесконечно малой, если для любого   существует такое значение   , что каждое следующии за ним значение   будет по абсолютной величине меньше   .

Если   - бесконечно малая то говорят, что   стремится к нулю, и пишут:   .

Бесконечно большие.

Переменная x называется бесконечно большой, если для всякого положительного числа cсуществует такое значение   , что каждое следующее за ним x будет по абсолютной величине больше   . Пишут: 

Величина, обратная к бесконечно большой, есть величина бесконечно малая, и обратно. 

Билет 7

А)Прямая на плоскости (общее уравнение прямой, уравнение прямой проходящей через данную точку и параллельная данной прямой)

Общее уравнение прямой линии на плоскости в декартовых координатах:

где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B)называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.

При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде :

. Уравнение прямой, проходящей через данную точку A(x₁, y₁) в данном направлении, определяемом угловым коэффициентом k,

y - y₁ = k(x - x₁).     (1)

Б)Функции. Способы их задания. (свойства)

Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.

При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.

Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.

Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.

Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.

Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.

Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.

Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.

Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.

Функция может быть определена разными формулами на разных участках области своего задания.

Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.

Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.

Билет 8