7.5. Основне рівняння динаміки обертального руху

Тіло, що обертається навколо осі z (рис. 7.7), розіб'ємо умовно на N елементарних об'ємів масами Δm_i. Складова моменту імпульсу -го елементарного об'єму, паралельна осі z, дорівнює

Розкривши подвійний добуток знаходимо, що . Тоді:

(7.25)

Складова моменту імпульсу всього тіла, паралельна осі z, дорівнює сумі складових моментів імпульсу відносно цієї осі всіх N елементарних об'ємів:

(7.26)

Величину

(7.27)

Рис. 7.7 називають моментом інерції тіла відносно осі обертан-

ня z. Таким чином, складова моменту імпульсу тіла паралельна осі обертання, дорівнює добутку моменту інерції цього тіла відносно тієї ж осі на кутову швидкість:

(7.28)

Продиференціюємо це рівняння за часом і врахуємо рівняння (7.24):

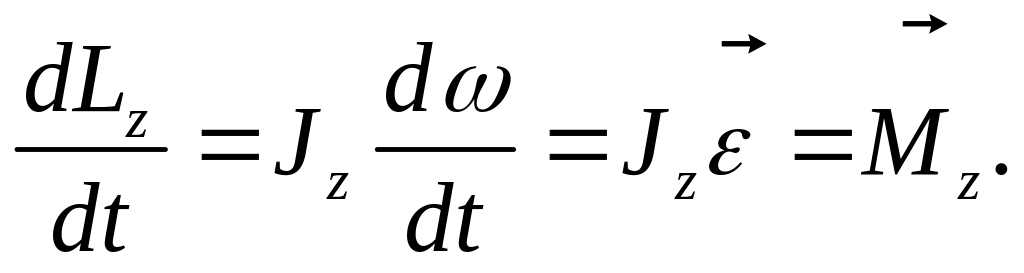(7.29) Це і є основне рівняння динаміки обертального руху твердого тіла. За фор-мою воно подібне до рівняння, що виражає другий закон Ньютона – основний закон динаміки поступального руху.

Оскільки для замкненої системи тіл

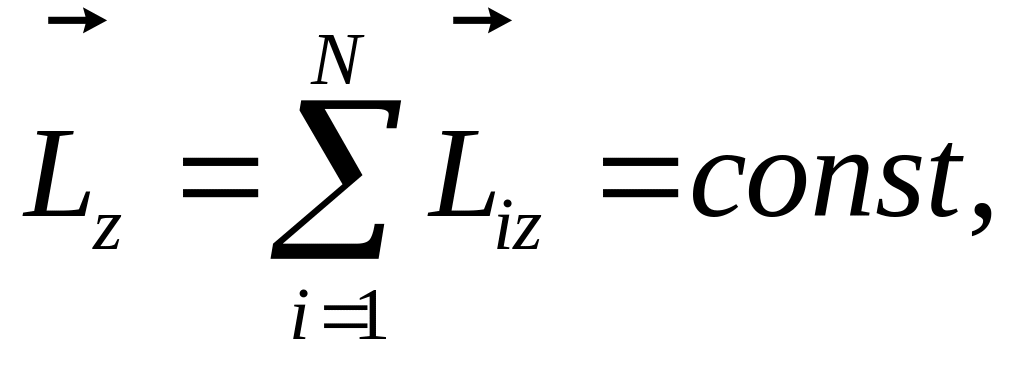
то для такої системи отримаємо:

(7.30)

звідки випливає вже відоме положення про те, що якщо на тіло не діє сумарна обертальна сила, то воно обертається без прискорення.

Розглядаючи момент імпульсу відносно осі як проекцію його складової на вісь обертання, рівняння (7.18), (7.24) – (7.29) варто записати в скалярній формі.

7.6. Вільні осі. Головні осі інерції. Моменти інерції різних тіл

При обертанні тіла навколо довільно обраної осі в загальному випад-ку вісь обертання або повертається, або переміщується відносно умовно не-рухомої системи відліку. Для того, щоб така вісь обертання залишалася в незмінному положенні, до неї необхідно прикласти певні зовнішні сили.

При обертанні однорідного симетричного тіла вісь обертання збері-гала б своє положення в просторі без впливу на неї ззовні. Вісь обертання тіла, положення якої в просторі зберігається без дії на неї будь-яких сил ззовні, називають вільною віссю тіла.

Для тіла будь-якої форми і з будь-яким розподілом маси існує три вза-ємно перпендикулярні осі, що проходять через центр інерції тіла, які мо-жуть служити вільними осями – їх називають головними осями інерції. У загальному випадку головні осі інерції тіла можуть бути обрані не в будь-якому довільному напрямку, а лише в певному, тобто вони фіксовані. В од-норідного тіла із площинною симетрією (наприклад, паралелепіпеда) фіксо-вані дві головні осі інерції. В однорідного тіла з осьовою симетрією (напри-клад, циліндра) фіксована лише одна з головних осей інерції (вісь цилінд-ра). В однорідного тіла із центральною симетрією (кулі) жодна з головних осей інерції не фіксована.

Моменти інерції відносно головних осей називають головними мо-ментами інерції тіла . У загальному випадку ці моменти різні:

Для тіла з осьовою симетрією два головні моменти інерції мають однакову величину, а третій відмінний від них: . Для тіла із цен-тральною симетрією всі три головні моменти інерції однакові:

Момент інерції тіла описується рівнянням (7.26). Масу речовини Δm_i можна виразити через густину речовини ρ і об'єм . Густина речовини в будь-якій точці виражається співвідношенням:

(7.31)

Тут вираз ΔV→0 означає, що об'єм стягується до тієї точки тіла, де визначається густина ρ, але ΔV≠0, а обмежується деяким мінімальним об'ємом, у межах якого можна говорити про густину речовини. Таким чи-ном, враховуючи (7.31), величину моменту інерції можна виразити рів-нянням:

(7.32)

Сума (7.32) тим точніша, чим менші ΔV_i. Отже, завдання знаходження мо-ментів інерції зводиться до обчислення інтеграла виду:

(7.33)

Для однорідних за густиною тіл

Р озглянемо кілька окремих прикладів роз-рахунку моментів інерції однорідних симетричних тіл.

7.6.1. Момент інерції циліндра. Відносно головної осі інерції ОО (рис.7.8) момент інерції

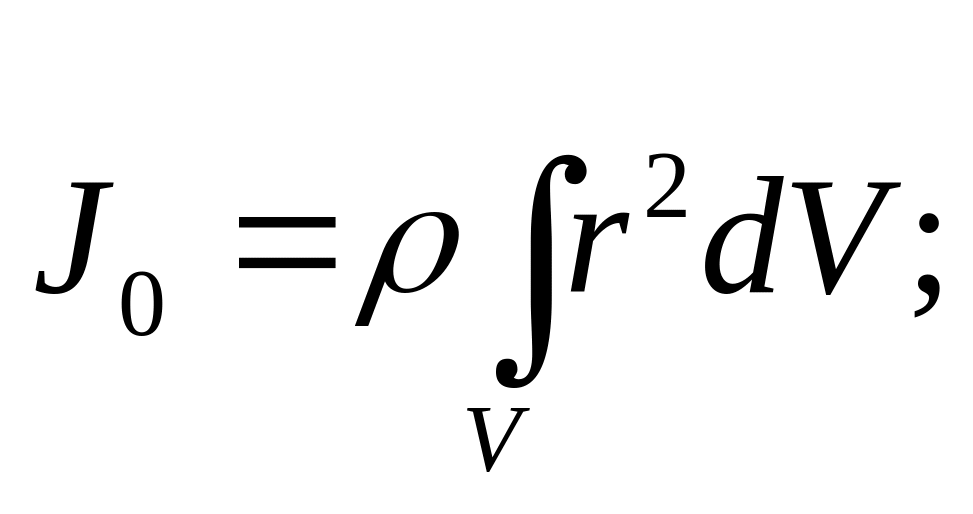
Рис.7.8 Для визначення моменту інерції відносно осі

z' скористаємося теоремою Штейнера: момент інерції відносно довіль-ної осі z, паралельної головній осі інерції, дорівнює сумі головного моменту інерції й добутку маси тіла т на квадрат відстані між осями:

(7.34)

(З доведенням теореми Штейнера можна ознайомитись за посібником [1]).

Вісь z' відстоїть від осі ОО на відстані . Тоді момент інерції циліндра відносно осі z' дорівнює:

.

7.6.2. Момент інерції товстостінного циліндра з порожниною відносно головної осі інерції.

Тут R₁ й R₂ – внутрішній і зовнішній радіуси циліндра відповідно:

– об’єм пустотілого циліндра.

Тоді:

7.6.3. Головний момент інерції тонкостінного циліндра. Для тонкостінного циліндра можна прийняти, що і , і

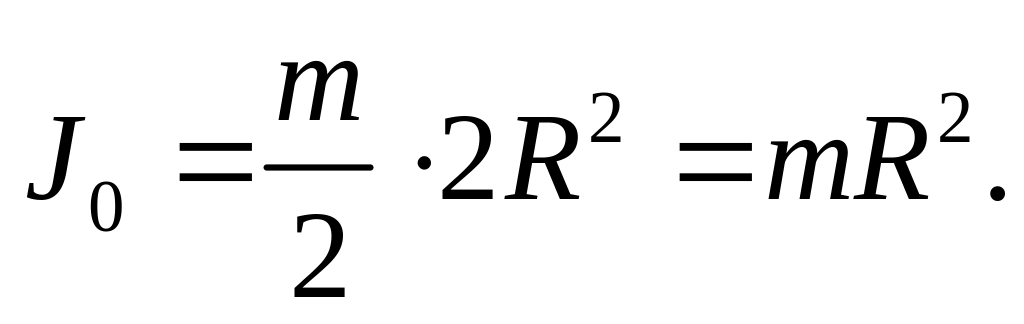
7.6.4. Момент інерції матеріальної точки m відносно довільної осі обертання z, що відстоїть на відстані від точки згідно з рівняннями (7.27) і (7.34) дорівнює: .

7 .6.5. Момент інерції тонкого довго-го стержня з постійним перетином S будь-якої форми. Елемент об'єму dV стержня при обертанні його навколо головної осі інерції ОО (рис. 7.9) дорівнює . Тоді

Рис.7.9

Тут L – довжина стержня. Згідно з теоремою Штейнера момент інерції стержня відносно осі z дорівнює:

7.6.6. Момент інерції тонкого диска відносно осі, що співпадає з діаметром диска. Елементарний момент інерції

(рис.7.10). За умови, що товщина диска , момент інерції диска від-носно осі Z знайдемо за рівнянням:

7.6.7. Головний момент інерції кулі. Для однорідної кулі . Елементарний момент інерції (рис. 7.11). Згідно з теоремою Піфагора . Сферична система симетрична, і середні значення

Рис. 7.10 Рис. 7.11

. Прийнявши, що , знаходимо:

.

І для диска, і для кулі – маса однорідного тіла, ρ – густина речовини.