7.3 Способы решения задач теории пластичности
Решение задач теории пластичности отдельно для напряжений и скоростей в общем случае невозможно, т.к. для 6 компонент тензора напряжений имеется только 3 статических уравнения. Поскольку ни статические, ни кинематические граничные условия в ОМД не бывают известны полностью, то приходится использовать смешанные граничные условия. Это приводит к необходимости совместного решения всех уравнений, входящих в системы типа (7.1). Поскольку все они включают дифференциальные уравнения в частных производных, а также нелинейные уравнения пластичности, то получение точных решений «в квадратурах», т.е. в виде формул, состоящих из различных функций, не представляется возможным. Поэтому разработаны разнообразные приближенные методы, которые можно условно разделить на три класса:
1.Численные методы;
2.Прямые методы получения решений на основе экстремальных принципов мсс;
3.Уменьшения числа независимых переменных и искомых функций.
Условность подобной классификации в том, что во всех методах используются приемы других методов. Например, в прямых методах может уменьшаться число искомых функций и могут применяться численные методы и т.п.
В настоящее время самыми популярными численными методами
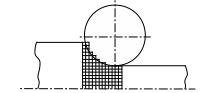
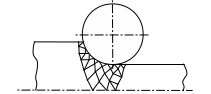
в практике инженерных расчетов являются метод конечных разностей (МКР), метод конечных элементов (МКЭ) и метод граничных элементов (МГЭ). Различие между ними наиболее ярко проявляется в способе дискретизации области, в которой ищется решение. В МКР область дискретизируется, как правило, посредством регулярной сетки, шаг которой постоянен или меняется по несложному закону. Форма ячеек предопределена выбором системы координат. Например, при т.н. «плоской» прокатке в декартовой системе координат дискретизация МКР будет иметь вид, показанный на рисунке 7.3а). Для той же задачи дискретизация МКЭ изображена на рисунке 7.3б), а МГЭ – на рисунке7.3в) (даны только верхние половины симметричных областей).
Очевидным недостатком МКР является то, что особенности геометрии исследуемой области могут быть учтены только в околограничных узлах. Уменьшение шага сетки с целью лучшей аппроксимации часто дает решение, не сходящееся к точному решению исходного дифференциального уравнения. Поэтому построение сходящейся разностной схемы - главная и наиболее сложная проблема МКР. В связи с тем, что в ОМД приходится исследовать области со сложными, криволинейными границами, МКР здесь не нашел широкого применения.
К сожалению МГЭ, весьма успешно применяющийся для решения задач теории упругости (см.п.5.12), мало пригоден для решения нелинейных задач теории пластичности. Известна возможность использования МГЭ к нелинейным задачам посредством итерационных процедур [38], однако решаемые задачи должны иметь достаточно слабую нелинейность. Поэтому в настоящее время самым эффективным методом решения пластических задач признан МКЭ.
Прямые методы подразделяются на вариационные и энергетичес-
а)
б)
в)
Рисунок 7.3 − Способы дискретизации области исследования
кие. Последние, в свою очередь, делятся на «метод работ» и метод верхней оценки (МВО).
Особенность всех прямых методов состоит в том, что решение задачи получают, минуя процедуру интегрирования системы дифференциальных уравнений, описывающих данную задачу. При этом вариационными методами получают функции, приближенно удовлетворяющие исходной системе уравнений, а энергетическими – только некоторые, важнейшие параметры решения (в основном – усилия деформирования).
Сущность вариационного метода состоит в замене исходной системы дифференциальных уравнений и граничных условий, описывающих данную задачу, эквивалентным функционалом. Исследуя этот функционал на экстремум, можно получить приближенное решение данной задачи [4].
Функционал – это числовая функция, ставящая в соответствие каждой функции из данного класса некоторое число [39]. Простейшим примером функционала является определенный интеграл с фиксиро-ванными пределами:
.
Например, в классе полиномов этот функционал будет иметь такие числовые значения:
и
т.д.
В соответствии с вариационными принципами МСС экстремальные значения у функционалов будут при подстановке в них тех функций, которые соответствуют действительным полям напряжений, скоростей и т.д. Отыскиваются эти функции методами вариационного исчисления, откуда и название метода.
Метод работ, называемый также методом баланса работ или мощностей, а также энергетическим методом, основан на законе сохранения энергии. Составляется уравнение равенства работ или мощностей внешних активных сил (деформирующих усилий), внешних сил трения и внутренних сил (напряжений). Затем, зная перемещение инструмента, находится деформирующее усилие. Этот метод является весьма приближенным, т.к.:
1) связь между напряжениями и деформациями берется по теории малых упруго-пластических деформаций;
2) напряжение трения τк никогда не бывает известным точно и его приходится принимать в соответствии с каким-либо законом трения;
3) для получения функций приращения перемещений (или скоростей) используют простейшие поля, разбивая очаг деформации на ряд областей, внутри которых деформация считается однородной. Для повыше-ния точности вводится работа сдвига на поверхностях разрывов.
Ясно, что результаты существенно зависят от того, насколько хорошо исследователь представляет картину течения металла в очаге деформации.
Метод верхней оценки (МВО) является модификацией энергетического метода. Очаг деформации разбивается на жесткие блоки, внутри которых деформация считается отсутствующей, а формоизменение осуществляется посредством относительного сдвига этих блоков.
Следовательно, действительное непрерывное поле скоростей заменяется достаточно произвольным разрывным кусочно-линейным. На основе закона сохранения энергии составляется уравнение баланса мощностей внешних и внутренних сил, из которого находится усилие деформирования. При этом считается, что полученная таким образом нагрузка является верхней оценкой этого параметра. Основанием для такой уверенности являются теорема о минимальных свойствах действительного поля скоростей (см. п.6.12).
Подробно вышеуказанные методы рассматриваются в курсе «Теория ОМД».