8.10 Определение величины и направления главных компонент тензора

Три главных значения тензора 2-го ранга являются тремя корнями характеристического уравнения (8.8). Следует по матрице а_ik вычислить I_i(а_ik ) и решить кубическое уравнение, все три корня которого в случае симметричного тензора будут действительными [11].

Для определения направления следует воспользоваться системой уравнений (8.6). Вектор считаем единичным, поэтому проекциями будут:

Следовательно:

(8.9)

Вместо одного из уравнений (8.9) можно использовать условие нормировки единичного вектора (уравнение Эйлера):

8.11 Скалярные, векторные и тензорные поля

В отличие от физических полей (электромагнитного и т.д.) в математике под полем понимают часть пространства, в каждой точке которого задана скалярная, векторная или тензорная величина. Соответ-ственно говорят о скалярных, векторных или тензорных полях, отвлекаясь от физической природы этих переменных величин.

Примеры: распределение температур в нагретом теле – скалярное поле, поскольку температура - скаляр; распределение скоростей частиц движущейся жидкости – векторное поле, поскольку скорость - вектор; распределение напряжений в деформируемом теле – тензорное поле, т.к. напряженное состояние является величиной тензорной.

Поля задаются функциями координат и времени. В этом случае они называются нестационарными:

Если поле не зависит от времени, то оно называется стационарным:

Поле также можно задавать радиус-вектором точек пространства:

8.12 Поверхности уровня и градиент скалярного поля

Геометрической характеристикой скалярного поля являются поверхности уровня [43].

Поверхность уровня - это геометрические места точек, в которых значения данной скалярной величины одинаковы:

f (x, y, z) = c (где с = соnst),

Например: изобары, изотермы (рис.8.4).

Задача: построить поверхности уровня плоского скалярного поля φ = =x² - y². Решение: x² - y² = с . При с = 0 получаем пару прямых:

у = х ; у = z . При с ≠ 0 получаем семейство гипербол (рис.8.4).

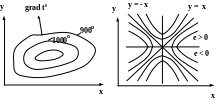
Рисунок 8.4 − Поверхности (линии) уровня

Градиент – вектор, проекциями которого являются частные производные данной скалярной функции:

Градиент направлен по нормали к поверхности уровня в сторону возрастания поля. Он показывает направление и величину наиболь-шего изменения скалярного поля в данной точке.

Пример: найти градиент поля в точке М (2;-5;1).

Решение:

В точке М: