КАФЕДРА ОБРОБКИ МЕТАЛІВ ТИСКОМ

І МЕТАЛОЗНАВТСВА

МЕТОДИЧНІ ВКАЗІВКИ

до виконання семестрового завдання по курсу:

«ТЕОРІЯ ПЛАСТИЧНОГО ПЛИНУ ТВЕРДИХ ТІЛ»

(для студентів за фахом 6.090 404)

Затверджено на засіданні

кафедри ОМТ і М

протокол № 7 від 14.03.2001

Затверджено на засіданні

Методичної Ради

Протокол № 4 від 19.01.20001

УДК 621.771.001 (075.8)

Методичні вказівки до виконання семестрового завдання по курсу «Теорія пластичного плину твердих тіл» (для студентів фаху 6.090 404 «Обробка металів тиском») / Укл. Данько В.М. – Алчевськ, ДГМІ, 2001. – 21 с.

Викладено основні теоретичні положення та послідовність дослідження напруженого стану в точці. Наведені приклади розрахунків на всіх етапах дослідження.

Укладач: В.М. Данько, доц..

Відп. за вип.. В.О. Луценко, доц..

Відповідальний редактор М.П. Козін, доц..

1. Опис напруженого стану в точці

Як відомо, напружений стан в точці – це сукупність напруг на всіляко орієнтованих площадках, що проходять через цю точку. Для визначення напруг на довільно орієнтованій площадці, як це було доведено ще О. Коші, потрібно знайти напруги на 3-х взаємно ортогональних площадках, що також проходять через цю точку.

Дев’ять проекцій цих 3-х так званих напруг на вісі системи координат називаються компонентами напруженого стану в точці. Отже напружений стан у точці не може бути описаний вектором, який має тільки три компоненти у трьохмірному просторі.

Для опису напруженого стану в точці використовується перемінна величина більш складної структури – тензор.

Тензор (2-го рангу) – це змінна величина, котра визначена в будь якій системі координат n² компонентами (де n – розмірність простору):

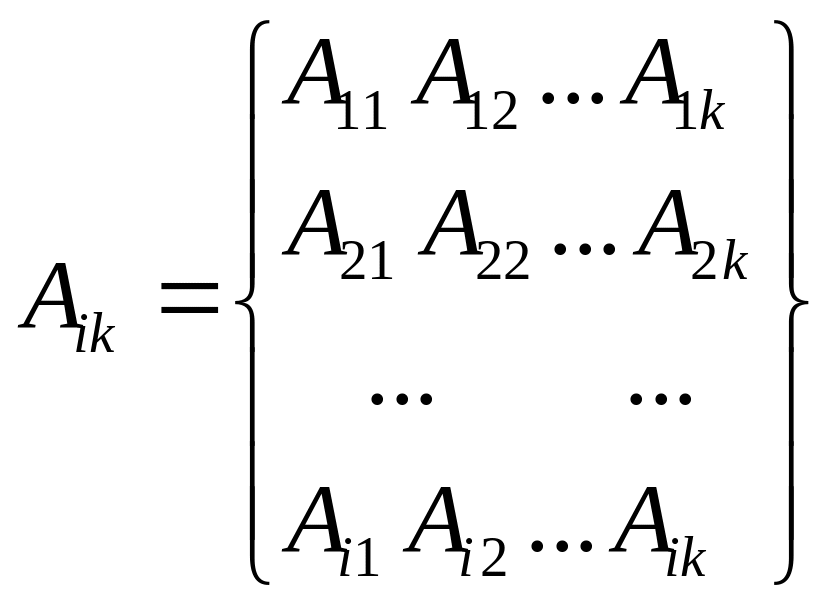, (1)

які при поворотах системи координат перетворюються по залежності:

(2)

де I, k, l, m = 1, 2 ... n

У (2) – направляючі косинуси переходу від старої системи координат до нової. [1]. Наприклад – це косинус кута α між другою віссю нової системи координат та третьої старої (рис. 1). За звичай вісі нової системи координат позначаються штрихами, а старої – без штрихів.

Тут. як і завжди в подальшому, мається на увазі прямокутна Декартові система координат.

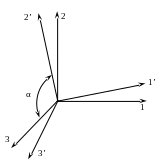
Рисунок 1.

Тензори другого рангу зображуються у вигляді матриці (1) або, в скороченому вигляді, як буква з двома індексами:

,

де розуміється зміна індексів від 1 до n.

Кількість компонент тензора залежить від розмірності простору n та рангу тензора p:

У скалярів: , тобто це тензори нульового рангу.

У векторів: , тобто це тензори першого рангу.

Тензори другого та більш високих рангів власних найменувань не мають. Оскільки компонентами напруженого стану в точці є нормальні σ_х, σ_y, σ_z та тангенційні τ_xy, τ_yz, τ_zx, τ_yx, τ_zy, τ_xz напруги, то тензор напруги має матрицю:

(3)

На гранях елементарного об’єму компоненти напруженого стану мають вигляд (рисунок 2).

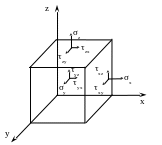
Рисунок 2

Компоненти напруженого стану залежать від вибору системи координат (який довільний) і змінюються при її зміні (2). Тому необхідно вміти визначити ці компоненти при переході від однієї системи координат до іншої.

2. Послідовність аналізу напруженого стану в точці

Для проведення цього аналізу треба мати тензор напруг.

Наприклад:

Крім того індивідуальне завдання передбачає три направляючих косинуса нової системи координат відносно старої, наприклад:

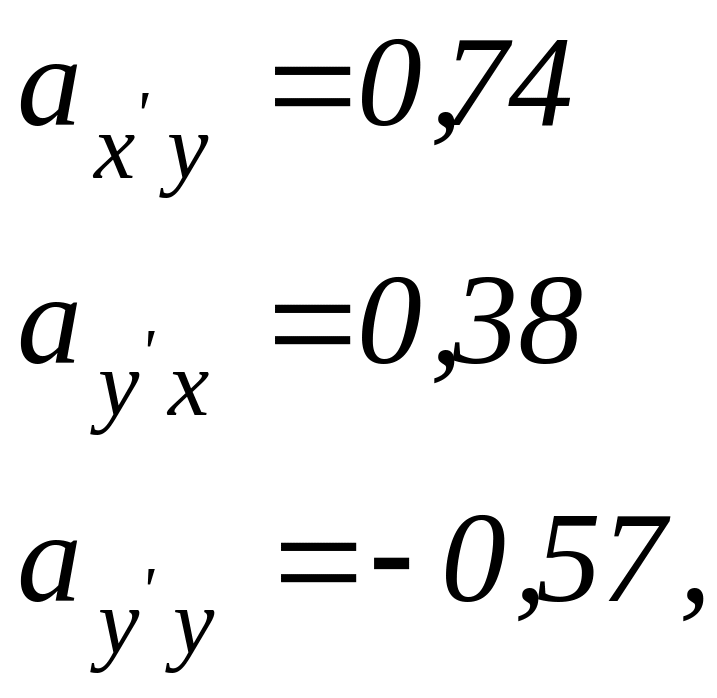
та три косинуса нормалі довільної площадки, на якій потрібно визначити напруги. Наприклад:

Спочатку треба визначити шість направляючих косинусів, яких не вистачає для розрахунку компонент тензора σ_ik у новій системі координат по (2).

Потім визначити ці компоненти, підставляючи у (2) значення старих компонент та направляючих косинусів. Для перевірки застосувати базисні інваріанти тензора напруги.

Розрахувати абсолютні величини головних напруг за допомогою характеристичного рівняння тензора σ_ik та визначити їх напрями.

Вирахувати максимальні тангенційні та октаедричні напруги, інтенсивності нормальних та тангенційних напруг.

Вирахувати повну напругу на довільно орієнтованій площадці та її нормальні і тангенціальні складові.