Библиографический список

1. Карасёв А.И. , Аксютина З.М. , Савельева Т.И. Курс высшей математики для экономических вузов. Ч.П.М.: Высшая школа , 1983.

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 1979.

3. Венецкий И.Г. , Венецкая В.И. Основные математико-статистические понятия и формулы в экономическом анализе: Справочник . М.: Статистика, 1979.

Приложение 1

Образец выполнения индивидуального задания

Методику построения интервального ряда распределения и вычисления его основных статистических характеристик рассмотрим на следующем примере.

Пример. Производительность труда на одного работающего (млн. руб.) по 50 предприятиям отрасли за некоторый период была следующей:

4,20	3,80	3,99	3,82	4,23	4,03	4,06	3,94	4,24	4,16
4,10	3,84	4,18	4,03	4,17	3,91	4,15	3,98	4,12	3,85
4,28	3,93	4,01	3,93	4,15	3,96	3,70	3,89	3,91	4,11
4,01	4,11	3,98	3,79	3,78	3,99	3,98	4,02	3,92	4,09
4,08	4,29	4,01	4,03	4,05	4,03	3,93	3,95	3,95	3,90

1. Построим интервальный ряд распределения с равными интервалами.

Определяем в ряду наблюдений минимальный и максимальный варианты:

x_min = 3,70; x_max = 4,29.

Определяем размах вариации R= x_max - x_min = 4,29-3,70= 0,59.

Используя формулу (1), найдём ширину интервала:

Устанавливаем полную шкалу интервалов:

a₁ = x_min - h/2 = 3,70 - 0,05 = 3,65

a₂ = a₁ + h = 3,65 + 0,1 = 3,75

a₃ = a₂ + h = 3,75 + 0,1 = 3,85 и т.д.

Таким образом, первый интервал будет [3,65; 3,75] , второй [3,75; 3,85] и т.д.

Верхние и нижние границы интервалов записываем в первую графу табл. 1 до тех пор, пока в последний (в данном случае - седьмой) интервал попадёт значение x_max = 4,29.

Производим группировку результатов наблюдений по интервалам, проставляя черточки в графе 2 таблицы 1 напротив соответствующих интервалов. Общее количество черточек, проставленных против интервала, даст его частоту (графа 3). В графе 4 (табл. 1) подсчитаем накопленные частоты.

Таблица 1

Интервалы	Подсчёт частот	Частоты	Накопленные частоты
3 ,65 - 3,75		1	1
3 ,75 - 3,85		6	7
3 ,85 - 3,95		11	18
3 ,95 - 4,05		15	33
4 ,05 - 4,15		9	42
4 ,15 - 4,25		6	48
4 ,25 - 4,35		2	50
		S = 50

2. Начертим графики полигона, гистограммы, кумуляты.

При изображении интервального вариационного ряда в виде полигона предполагается, что в пределах интервалов частоты распределены равномерно, поэтому их можно отнести к тому значению признака, которое находится в центре интервала:

Практически это означает, что полигон можно получить, соединяя отрезками прямых точки с координатами (x_i; m_i) (см. рис. 1).

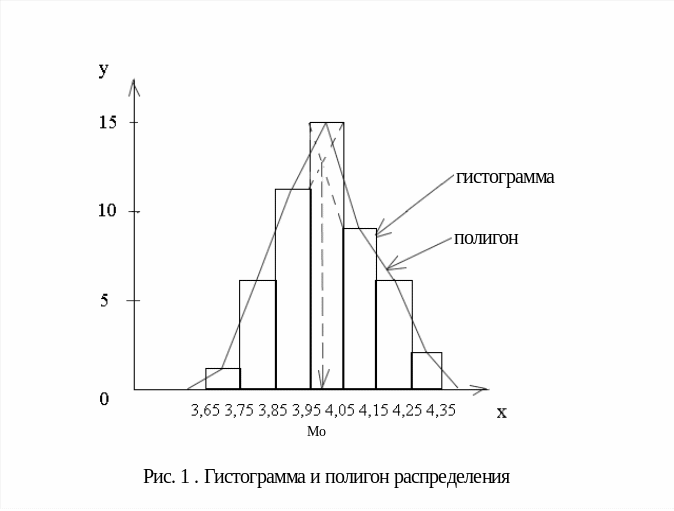
При построении гистограммы на оси абсцисс откладываются интервалы, а на оси ординат - частоты. Гистограмма состоит из прямоугольников с высотами m_i , основания которых соответствуют интервалам изменения признаков.

Для построения кумуляты используются накопленные частоты m_{i нак} (см. табл. 1). При этом на оси абсцисс откладываются значения признака, а на оси ординат - накопленные частоты, причём накопленная частота интервала относится к его верхней границе, а накопленная частота нижней границы первого интервала равна нулю (рис. 2).

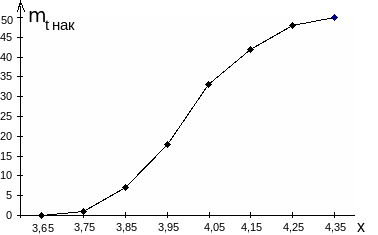
Рис. 2. Кумулятивная кривая

3. Для определения статистических характеристик исследуемого вариационного ряда удобно использовать данные расчетной таблицы 2.

Вычислим среднюю величину производительности труда на одного работающего по формуле (2):

млн. руб.

Правильность вычисления средней можно легко проверить:

å(x_i -`x ) m_i = - 2,666 + 2,666 = 0 (табл. 2 гр. 6 ).

Вычислим по формуле (6) и данным гр. 7 (табл. 2) дисперсию

(млн. руб.)²,

а также среднее квадратическое отклонение:

млн. руб.

Следует помнить, что должно иметь место соотношение: R>s. В нашем случае оно выполняется.

По формуле (9) определим коэффициент вариации (в процентах):

Vs=S/X×100%=0.138/4.002 * 100%=3.4%

Таблица 2

Интервалы	Частоты	Центры		Расчетные графы
ai - bi	mi	интервалов	miнак		ximi	(xi -`x) mi	(xi-`x)^2mi	(xi-`x)^3mi	(xi-`x)^4mi
		xi
3.65-3.75	1	3.7	1		3.7	-0.302	0.0912	-0.0275	0.0083
3.75-3.85	6	3.8	7		22.8	-1.212	0.2448	-0.0494	1.0100
3.85-3.95	11	3.9	18		42.9	-1.122	0.1144	-0.0117	0.0012
3.95-4.05	15	4.0	33		60.0	-0.030	0	0	0
4.05-4.15	9	4.1	42		36.9	0.882	0.0864	0.0085	0.0008
4.15-4.25	6	4.2	48		25.2	1.188	0.2352	0.0466	0.0092
4.25-4.35	2	4.3	50		8.6	0.596	0.1776	0.0529	0.0158
Итого	50	-----	-----		200.1	S=0	S=0.9496	0.0194	0.0453

Используя формулу (12) и графу 8 таблицы 2, определим величину асимметрии:

.

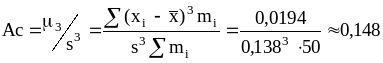С помощью формулы (13) и графы 8 таблицы 2 определим величину эксцесса:

.

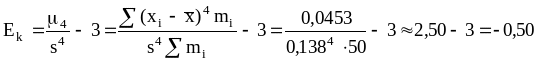Для определения моды найдем модальный интервал: [3.95; 4.05], так как ему соответствует наибольшая частота, равная 15. Подставим в формулу (4) aмo=3.95, h=0.1, mмo=15, mмo-1=11, mмo+1=9, получаем:

Мo=3.95+0.1(15-11)/(2*15-11-9)=3.95+0.4/10=3.99 млн.руб.

Для вычисления медианы воспользуемся формулой (3). По накопленным частотам mi определим первую накопленную частоту , равную или большую mi/2=50/2=25 . Она равна 33 . Следовательно , медианным является интервал [3.95;4.05] и aме=3.95 , h=0.1; mме=15, mме-1=18 .

Mе=3.95+0.1(25-18)/15=3.95+0.7/15=3.997 млн. руб.

4. Для исследуемого вариационного ряда Ас=+0.148>0, следовательно, имеет место небольшая правосторонняя асимметрия: слева от вершины (рис.1) расположена более короткая ветвь , т.е. в ряду преобладают варианты, большие .

Было доказано, что Ек=-0.5 , следовательно, данное распределение является плосковершинным: кривая распределения по сравнению с нормальной кривой является менее крутой.

Вычислим средние ошибки (D) асимметрии и эксцесса:

.

Наличие асимметрии и эксцесса можно считать статистически существенным, т.е. сформированным под воздействием не только случайных причин, но и какого-либо неслучайного фактора, если абсолютная величина каждого из них превышает абсолютную величину своей ошибки, по крайней мере, в три раза:

Ас/DAc > 3 ; Eк/ DEk > 3 .

В нашем случае:

;

Таким образом, практически с полной достоверностью (с доверительной вероятностью 0.9973) наблюдаемые правостороннюю асимметрию и плосковершинность распределения можно считать статистически несущественными, т.е. сдвиг вершины распределения вправо и вниз произошел под воздействием случайных факторов.

5. Укрупнить рисунок 1 и выполнить требования п.5 задания самостоятельно.

6. Очень часто на практике возникает необходимость оценки степени близости эмпирического распределения одному из теоретических законов распределения. При обработке экономических данных в качестве теоретического распределения чаще всего используется нормальный закон.

Критерий Пирсона или c² имеет наибольшее применение при проверке согласованности теоретической и эмпирической кривых распределения. Наблюдаемое значение критерия вычисляют по формуле:

, (14)

где m_эi - эмпирическая частота i-ого интервала ; m_тi- теоретическая частота i -ого интервала ; L - число интервалов .

c² - распределение зависит от числа степеней свободы:

n = L - r -1 , ( 15 )

где r - число параметров предполагаемого теоретического закона, оцениваемых по выборке.

Применение критерия Пирсона c² требует выполнения следующих условий :

1. объем выборки должен быть достаточно велик ( n³ 50) ;

2. сумма эмпирических частот должна быть равна сумме теоретических частот ;

3. интервалы должны быть заполнены ( в каждом интервале не менее 5-10 наблюдений) .

Теоретическое нормальное распределение определяется двумя параметрами: МХ - математическим ожиданием и s² - дисперсией, которые и определяют положение и форму кривой.

Для построения теоретической кривой распределения предположим , что `x » MX ,a S =s ,поэтому r = 2 и число степеней свободы равно n = L -3.

Вероятность попадания случайной величины Х в интервал (ai,bi) вычисляется по интегральной теореме Лапласа:

Pi = P(ai £ х £ bi ) =Ф(t2i)-Ф(t1i), (16)

где t_1i = (ai -`х) / s ; t<sub>2i</sub> = (bi -`х) / s ,

Ф(t) - функция Лапласа (Приложение 2).

При определении теоретических частот удобно пользоваться таблицей 3.

Таблица 3

Интервалы	mэi	t1i	t2i	Ф(t1i)	Ф(t2i)	Pi	n×Pi	mti
3.65-3.75	1	-2.65	-1.82	-0.4946	-0.4656	0.039	1.95	2
3.75-3.85	6	-1.82	-1.10	-0.4656	-0.3643	0.101	5.05	5
3.85-3.95	11	-1.10	-0.38	-0.3643	-0.1480	0.216	10.80	11
3.95-4.05	15	-0.38	0.35	-0.1480	0.1368	0.285	14.25	14
4.05-4.15	9	0.35	1.07	0.1368	0.3577	0.221	11.05	11
4.15-4.25	6	1.07	1.80	0.3577	0.4641	0.106	5.30	5
4.25-4.35	2	1,80	2.52	0.4641	0.4941	0.030	1.50	2
Итого	50	------	------	----------	---------	--------	49.9	50

На уровне значимости a =0.05 проверим гипотезу о нормальном законе распределения исследуемого вариационного ряда при помощи критерия c² (14). Расчет наблюдаемого значения c²_н приведен в таблице 4. Поскольку в первом и последнем интервалах число наблюдений меньше 5 , объединяем первые два и последние два интервала. Таким образом, число интервалов L становится равным 5.

Таблица 4

Интервалы	mэi	mтi	(mэi-mтi)^2	(mэi-mтi)^2 / mтi
3.65-3.75	1 ü	2 ü	0	0
	ý	ý
3.75-3.85	6 þ	5 þ
3.85-3.95	11	11	0	0
3.95-4.05	15	14	1	0.071
4.05-4.15	9	11	4	0.364
4.15-4.25	6 ü	5 ü
	ý	ý
4.25-4.35	2 þ	2 þ	1	0.143
Итого	50	50		0.578

По таблице c² - распределения (Приложение 3) на уровне значимости a=0.05 и числе степеней свободы n =L - 3= 5 - -3=2 определяем критическое значение критерия согласия c²_кр =5,991.Так как c²_н =0.578 <Хкр=5,9, нулевая гипотеза о случайном расхождении эмпирического и теоретического распределений не отвергается, т. е. производительность труда для данной совокупности предприятий подчиняется нормальному закону. Следовательно, можно считать, что колебания уровней производительности труда на предприятиях отрасли объясняются в основном случайными причинами.

Приложение 2

Таблица значений функции

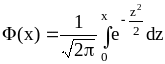
x	Ф(x)
0	0,000000
0,01	0,003989
0,02	0,007978
0,03	0,011967
0,04	0,015953
0,05	0,019939
0,06	0,023922
0,07	0,027903
0,08	0,031881
0,09	0,035856
0,1	0,039828
0,11	0,043795
0,12	0,047758
0,13	0,051717
0,14	0,055670
0,15	0,059618
0,16	0,063559
0,17	0,067495
0,18	0,071424
0,19	0,075345
0,2	0,079260
0,21	0,083166
0,22	0,087064
0,23	0,090954
0,24	0,094835
0,25	0,098706
0,26	0,102568
0,27	0,106420
x	Ф(x)
0,28	0,110261
0,29	0,114092
0,3	0,117911
0,31	0,121719
0,32	0,125516
0,33	0,129300
0,34	0,133072
0,35	0,136831
0,36	0,140576
0,37	0,144309
0,38	0,148027
0,39	0,151732
0,4	0,155422
0,41	0,159097
0,42	0,162757
0,43	0,166402
0,44	0,170031
0,45	0,173645
0,46	0,177242
0,47	0,180822
0,48	0,184386
0,49	0,187933
0,5	0,191462
0,51	0,194974
0,52	0,198468
0,53	0,201944
0,54	0,205402
0,55	0,208840
x	Ф(x)
0,56	0,212260
0,57	0,215661
0,58	0,219043
0,59	0,222405
0,6	0,225747
0,61	0,229069
0,62	0,232371
0,63	0,235653
0,64	0,238914
0,65	0,242154
0,66	0,245373
0,67	0,248571
0,68	0,251748
0,69	0,254903
0,7	0,258036
0,71	0,261148
0,72	0,264238
0,73	0,267305
0,74	0,270350
0,75	0,273373
0,76	0,276373
0,77	0,279350
0,78	0,282305
0,79	0,285236
0,8	0,288145
0,81	0,291030
0,82	0,293892
0,83	0,296731
0,84	0,299546
0,85	0,302338
0,86	0,305106
0,87	0,307850
0,88	0,310570
0,89	0,313267
0,9	0,315940
0,91	0,318589
0,92	0,321214
0,93	0,323814
0,94	0,326391
0,95	0,328944
0,96	0,331472
0,97	0,333977
0,98	0,336457
0,99	0,338913
1	0,341345
1,01	0,343752
1,02	0,346136
1,03	0,348495
1,04	0,350830
1,05	0,353141
1,06	0,355428
1,07	0,357690
1,08	0,359929
1,09	0,362143
1,1	0,364334
1,11	0,366500
1,12	0,368643
1,13	0,370762
1,14	0,372857
1,15	0,374928
1,16	0,376976
1,17	0,378999
1,18	0,381000
1,19	0,382977
1,2	0,384930
1,21	0,386860
1,22	0,388767
1,23	0,390651
1,24	0,392512
1,25	0,394350
1,26	0,396165
1,27	0,397958
1,28	0,399727
1,29	0,401475
1,3	0,403199
1,31	0,404902
1,32	0,406582
1,33	0,408241
1,34	0,409877
1,35	0,411492
1,36	0,413085
1,37	0,414656
1,38	0,416207
1,39	0,417736
1,4	0,419243
1,41	0,420730
1,42	0,422196
1,43	0,423641
1,44	0,425066
1,45	0,426471
1,46	0,427855
1,47	0,429219
1,48	0,430563
1,49	0,431888
1,5	0,433193
1,51	0,434478
1,52	0,435744
1,53	0,436992
1,54	0,438220
1,55	0,439429
1,56	0,440620
1,57	0,441792
1,58	0,442947
1,59	0,444083
1,6	0,445201
1,61	0,446301
1,62	0,447384
1,63	0,448449
1,64	0,449497
1,65	0,450529
1,66	0,451543
1,67	0,452540
1,68	0,453521
1,69	0,454486
1,7	0,455435
1,71	0,456367
1,72	0,457284
1,73	0,458185
1,74	0,459071
1,75	0,459941
1,76	0,460796
1,77	0,461636
1,78	0,462462
1,79	0,463273
1,8	0,464070
1,81	0,464852
1,82	0,465621
1,83	0,466375
1,84	0,467116
1,85	0,467843
1,86	0,468557
1,87	0,469258
1,88	0,469946
1,89	0,470621
1,9	0,471284
1,91	0,471933
1,92	0,472571
1,93	0,473197
1,94	0,473810
1,95	0,474412
1,96	0,475002
1,97	0,475581
1,98	0,476148
1,99	0,476705
2	0,477250
2,02	0,478308
2,04	0,479325
2,06	0,480301
2,08	0,481237
2,1	0,482136
2,12	0,482997
2,14	0,483823
2,16	0,484614
2,18	0,485371
2,2	0,486097
2,22	0,486791
2,24	0,487455
2,26	0,488089
2,28	0,488696
2,3	0,489276
2,32	0,489830
2,34	0,490358
2,36	0,490863
2,38	0,491344
2,4	0,491802
2,42	0,492240
2,44	0,492656
2,46	0,493053
2,48	0,493431
2,5	0,493790
2,52	0,494132
2,54	0,494457
2,56	0,494766
2,58	0,495060
2,6	0,495339
2,62	0,495603
2,64	0,495855
2,66	0,496093
2,68	0,496319
2,7	0,496533
2,72	0,496736
2,74	0,496928
2,76	0,497110
2,78	0,497282
2,8	0,497445
2,82	0,497599
2,84	0,497744
2,86	0,497882
2,88	0,498012
2,9	0,498134
2,92	0,498250
2,94	0,498359
2,96	0,498462
2,98	0,498559
3	0,498650
3,2	0,499313
3,4	0,499663
3,6	0,499841
3,8	0,499928
4	0,499968
4,5	0,499997
5	0,500000

Приложение 3.

Таблица c²-распределения.

Число степеней		Уровень значимости a
свободы n	0,010000		0,02	0,05
1	6,634891		5,411904	3,841455
2	9,210351		7,824071	5,991476
3	11,344882		9,837411	7,814725
4	13,276699		11,667844	9,487728
5	15,086317		13,388224	11,070483
6	16,811872		15,033197	12,591577
7	18,475324		16,622430	14,067127
8	20,090159		18,168201	15,507312
9	21,666048		19,678978	16,918960
10	23,209287		21,160752	18,307029
11	24,725022		22,617895	19,675153
12	26,216964		24,053935	21,026055
13	27,688184		25,471492	22,362027
14	29,141163		26,872730	23,684782
15	30,577951		28,259488	24,995797

Составитель

Виктор Борисович Королёв