Властивості скалярного добутку

1. Переставна властивість .

2. Розподільна властивість .

3. Сполучність відносно скалярного множника .

4. Необхідна і достатня умова ортогональності () двох векторів: два вектори і ортогональні тоді і тільки тоді, коли .

5. З формули (2.3) також випливає:, якщо 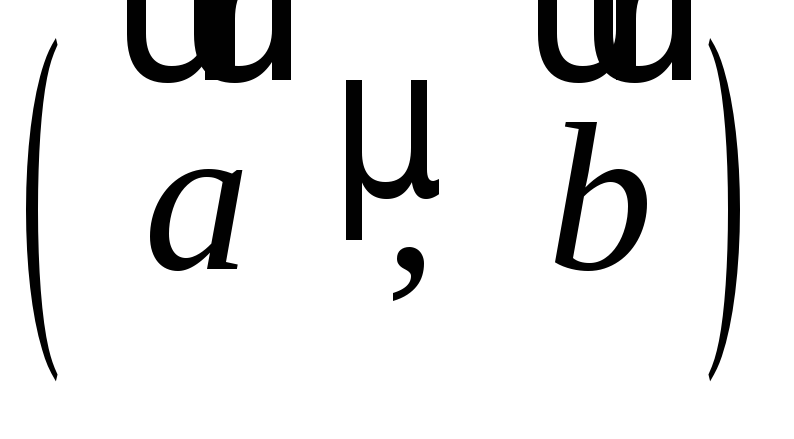гострий;, якщо тупий.

Теорема 2.14. Якщо два вектори і задані своїми прямокутними декартовими координатами , , то їх скалярний добуток обчислюється за формулою .

Наслідки теореми 2.14.

1. Довжину вектора можна обчислити за формулою .

2. Кут між векторами і обчислюється за допомогою рівності

. (2.6)

3. Напрямні косинуси вектора можна обчислити за формулами

, , .

З останнього твердження випливає рівність, яку називають характеристичною властивістю напрямних косинусів .

Приклад. Знайти кут між векторами та .

Розв’язання. Знайдемо скалярний добуток векторів

, а також їх модулі: , . Тоді (згідно з формулою (2.6)). Тоді .

§ 8. Векторний добуток

Векторним добутком двох векторів і називається вектор, який позначається символом і визначається трьома умовами:

1) вектор перпендикулярний кожному з векторів - співмножників

;

2) вектори утворюють праву трійку;

3) модуль вектора дорівнює площі паралелограма, побудованого на векторах і як на сторонах (рис. 2.7) .

Властивості векторного добутку

1. Антикомутативність .

2. Сполучність відносно скалярного множника

.

3. Розподільна властивість .

4. Необхідна і достатня умова колінеарності двох векторів: два вектори і колінеарні тоді і тільки тоді, коли .

Теорема 2.15. Якщо вектори і задано їх прямокутними декартовими координатами , , то їх векторний добуток можна обчислити за формулою

.

Доведення. Обчислимо спочатку векторні добутки векторів прямокутного декартового базису. За властивістю 4 векторного добутку, маємо

.

Розглянемо тепер добуток (рис.2.6). Його напрям співпадає з напрямом вектора (адже , , вектори утворюють праву трійку). Довжина вектора дорівнює площі побудованого на них як на сторонах квадрата, тобто 1. Отже . Тоді . Аналогічно доводиться, що

Перемножимо і як векторні суми, користуючись властивостями векторного добутку

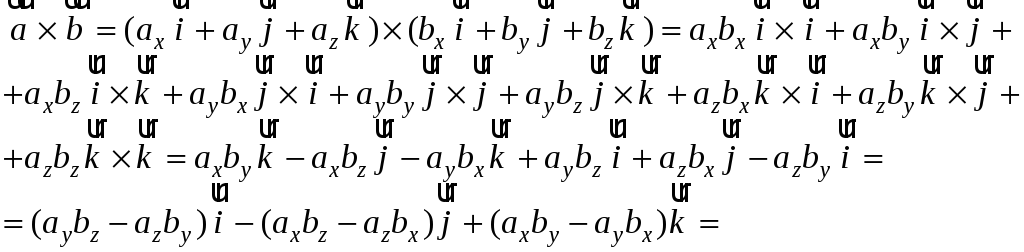
.Теорему доведено.

Приклад. Обчислити площу трикутника , якщо задано координати його вершин: .

Розв’язання. Будемо вважати, що трикутник побудовано на векторах і (рис. 2.8). Як бачимо, його площа дорівнює половині площі побудованого на цих же векторах паралелограма.

Знайдемо їх координати . Обчислимо їх векторний добуток і його довжину . Таким чином, (кв. од.).

§ 9. Мішаний добуток

Дано три вектори і . Знайдемо векторний добуток й отриманий вектор помножимо на скалярно. Добуток називають мішаним добутком векторів і .

Нехай вектори не компланарні й утворюють праву трійку (рис. 2.9). Тоді вектор напрямлений у той же бік відносно площини , що і вектор .

Знайдемо об’єм паралелепіпеда, побудованого на векторах і .

. Тоді

.

Якщо вектори і утворюють ліву трійку (наприклад, якщо на рисунку 2.9 вектор спрямувати в інший бік від площини ), то всі міркування залишаються такими ж, тільки , буде від’ємною, тобто, . Тому

(2.7)

(« + », якщо трійка векторів і - права, « - », якщо ліва). Таким чином, об’єм паралелепіпеда, побудованого на трьох не компланарних векторах, дорівнює модулю їх мішаного добутку. З теорем 2.14 та 2.15 випливає наступне твердження.

Теорема 2.16. Якщо вектори і задано їх прямокутними декартовими координатами , , , то їх мішаний добуток можна обчислити за формулою

.