Статистическая физика / Решение задач для практических занятий

Решение задач для практических занятий по курсу

«Статистическая физика»

Задача №1………………………………………………………………………….2

Задача №2…………………………………………………………………………3

Задача №3………………………………………………………………………….4

Задача №4………………………………………………………………………….6

Задача №5………………………………………………………………….………8

Задача №6………………………………………………………………………….9

Задача №7………………………………………………………………………...11

Задача №8………………………………………………………………………..13

Задача №9………………………………………………………………………..15

Задача №10…………………………………………………………………….…17

Задача №11……….………………………………………………………………19

Задача №12……………………………………………………………………….20

Задача №13……………………………………………………………………….22

Задача №14……………………………………………………………………….24

Задача №15…………………………………………………………………….…26

Задача №16…………………………………………………………………….…28

Задача №17…….…………………………………………………………………30

Задача №18……………………………………………………………………….33

Задача №19…………………………………………………………………….…36

Задача №20…………………………………………………………………….…38

Задача №21…………………………………………………………………….…40

Задача №22…………………………………………………………………….…42

Задача №23…………………………………………………………………….…44

1

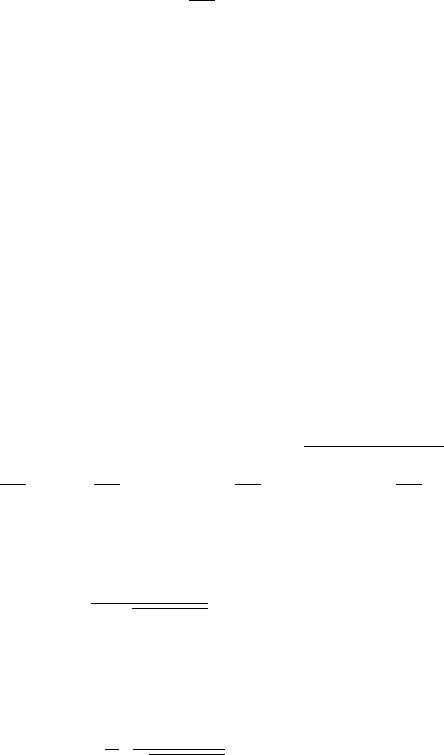
Задача № 1. Математический маятник совершает гармонические колебания по закону

где		– период колебаний маятника длиной	в поле
силы тяжести		с ускорением свободного падения	. Найти

вероятность того, что при случайном измерении отклонения

маятника на угол		это значение будет находиться в интервале
.
Решение:
Искомая	вероятность			,	где	–
время нахождения маятника в интервале углов						. Фактор
2 в определении		вероятности	связан с	тем,	что	период
колебаний	маятника определяется временем возвращения его в

начальное состояние.

Из закона колебаний следует, что

Следовательно,

Подставляя это выражение в определение искомой вероятности, находим

2

Задача № 2. Вероятность того, что для некоторой системы значения величин и лежат в интервале и , дается выражением

Считая, что	областями изменения переменных	и	являются
и	, найти нормировочную постоянную		, а также
найти вероятность того, что значение величины		будет находиться

в интервале	.
Решение:
Из условия нормировки вероятности		следует, что

Учтем далее значение интеграла

Следовательно,	. Поэтому вероятность			того,
что значение величины	будет находиться в интервале
равна

3

Задача № 3. При термоэлектронной эмиссии происходит вылет электронов с поверхности металла или полупроводника. Предполагая, что а) вылеты электронов являются статистически независимыми событиями и б) вероятность вылета одного

электрона за бесконечно малый промежуток времени								равна	,
где	– постоянная величина, определить вероятность вылета
электронов за время .
Решение:
Обозначим		через		искомую		вероятность вылета
электронов за время			, а через		– вероятность того, что за
время	не вылетит ни один электрон.
Пусть		–	вероятность		вылета	одного		электрона	за
бесконечно малое время , равная по условию б) задачи									.
Тогда вероятность того, что за малое время						электрон не вылетит,
равна	.
Таким образом, вылет				электронов за время				можно
рассматривать,		согласно		условию		а)	задачи,		как

последовательность двух возможных событий независимых

событий: вылет	электронов за время		с последующим
вылетом одного электрона за время		и вылет	электронов за

время с последующим не вылетом одного электрона за время :

С другой стороны, не вылет ни одного электрона за время соответствует тому, что не вылетает ни один электрон за

время с последующим не вылетом электрона за время :

Раскладываем теперь левые части полученных уравнений в ряд по степеням и устремляем . В результате получаем систему дифференциальных уравнений:

4

К полученной системе уравнений необходимо добавить начальные условия – вероятность вылета электронов в начальный момент времени равна нулю:

В этом случае решение полученной системы уравнений имеет вид распределения Пуассона

в чем нетрудно убедиться непосредственной подстановкой с учетом

.

5

Задача № 4. Предполагая, что в некоторой системе распределение числа частиц во времени имеет вид

где – неизвестная постоянная, определить среднеквадратичную флуктуацию числа частиц при условии, что среднее число частиц в единицу времени равно .

Решение:

По определению среднеквадратичная флуктуация числа

частиц есть	, где	, а средняя величина
равна:

Следовательно,

Учитывая, что

находим для заданного распределения

6

Учтем далее, что		поэтому из приведенных
соотношений следует

По условию задачи

, следовательно,

.

7

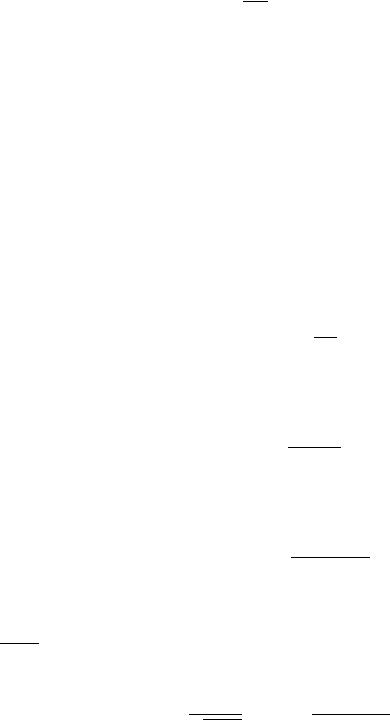
Задача № 5. Рассмотреть распределение Пуассона для числа частиц в предельном случае, когда .

Решение:

По определению распределение Пуассона для числа частиц

есть

Для случая используем формулу Стирлинга

. Следовательно,

Учтем далее, что

, поэтому

По условию задачи	, следовательно, учитывая, что при
малых значениях

находим с точностью до членов порядка

Отсюда

Теперь интегрируя эту вероятность

, находим

. В результате получаем распределение Гаусса:

8

Задача № 6. Найти уравнение состояния, внутреннюю энергию и теплоемкость квазиклассического идеального газа из частиц массы , используя каноническое распределение.

Решение:

Функция Гамильтона для идеального газа из частиц имеет

вид

Статистический интеграл по фазовому объему системы распадается на произведение интегралов по пространственным и импульсным переменным. Интеграл по координатам каждой

частицы дает объем	системы. Интеграл по импульсам
распадается на произведение	интегралов вида

Поэтому выражение для статистической суммы принимает вид

где – тепловая длина волны де Бройля. Свободная энергия системы определяется соотношением

Используя формулу Стирлинга				и выражение
для статистической суммы, находим

9

В константу объединены все члены, не зависящие от

и .

На основе термодинамического равенства

находим

Теплоемкость можно найти по формуле

Внутренняя (средняя) энергия может быть найдена с помощью любого из соотношений

10