ПОИТ Контрольная работа по высшей математике.№1

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет непрерывного и дистанционного обучения

Специальность: программное обеспечение информационных технологий

КОНТРОЛЬНАЯ РАБОТА

ПО ВЫСШЕЙ МАТЕМАТИКЕ №1

1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

1—10. Даны четыре вектора (а₁, а₂, а₃), (b₁, b₂, b₃),

(c₁, c₂, c₃) и (d₁, d₂, d₃) в некотором базисе. Показать, что векторы , , образуют базис, и найти координаты вектора в этом базисе.

(2,1,0), (4,3,-3), (-6,5,7), (34,5,-26).

Базисом в пространстве являются любые три некомпланарных вектора. Условием компланарности трех векторов является равенство их смешанного произведения нулю. Итак, находим

Значит, векторы некомпланарны и образуют базис. Составим систему уравнений (1.1) в координатном виде для нахождения координат вектора в этом базисе

Решим систему методом Крамера, для чего найдем . Определитель найден выше и = 62.

Имеем ; ; .

Следовательно .

11—20. Даны координаты вершин пирамиды A₁A₂A₃A₄. Найти: 1) длину ребра А₁А₂; 2) угол между ребрами А₁А₂ и А₁А₄; 3) угол между ребром А₁А₄ и гранью А₁А₂А₃; 4) площадь грани А₁А₂А₃; 5) объём пирамиды; 6) уравнения прямой А₁А₂; 7) уравнение плоскости А₁А₂А₃; 8) уравнения высоты, опущенной из вершины А₄ на грань А₁А₂А₃. Сделать чертёж.

А₁(6,6,2), А₂(5,4,7), А₃(2,4,7), А₄(7,3,0).

Находим координаты вектора

Длина ребра определяется как длина вектора

2. Угол  между ребрами и вычисляется по формуле

.

, ;

.

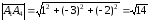Тогда ,

3. Угол  между ребром и плоскостью - это угол между вектором и его ортогональной проекцией на грань .

Из определения векторного произведения векторов следует, что вектор перпендикулярен грани :

А₁(6,6,2), А₂(5,4,7), А₃(2,4,7), А₄(7,3,0).

.

Как и в предыдущем пункте, находим

,

.

4. Площадь грани находим, используя геометрический смысл векторного произведения

.

5. Объем пирамиды 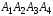численно равен одной шестой модуля смешанного произведения векторов , , (формула 1.4).

.

6. Составим уравнение прямой в пространстве, проходящей через две точки .

.

7. Для составления уравнения плоскости воспользуемся формулой (1.6), где - координаты , - координаты , - координаты .

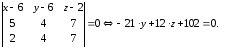
8. Искомые уравнения высоты получим из канонических уравнений прямой , где 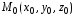- точка, лежащая на искомой прямой: - координаты вектора , параллельного искомой прямой. При этом в качестве точки возьмем точку , а в качестве вектора возьмем нормальный вектор плоскости , т.е. . Имеем .

А₁(6,6,2), А₂(5,4,7), А₃(2,4,7), .

9. Сделаем чертеж

30.Дано уравнение одной из сторон квадрата AB: x+3y-7=0 и точка пересечения его диагоналей P(0,-1). Найти уравнения трёх остальных сторон этого квадрата.

1) Найдем уравнение прямой, перпендикулярной прямой AB и проходящей через точку Р. Вектор нормали к прямой AB является направляющим для искомой прямой и имеет координаты . Следовательно каноническое уравнение прямой EF имеет вид:

2) Найдем точку E пересечения найденной прямой с прямой AB.

Координаты точки . Тогда координаты точки F исходя из того, что точка Р – середина отрезка EF: . Зная точку F найдем уравнение прямой CD, зная, что вектор нормали у прямых AB и CD совпадают по направлению.

Найдем уравнение прямой, проходящей через точку Р и параллельную прямой АВ:

Зная, что точки H1 и H2 лежат на этой прямой получим систему для нахождения координат точек, :

Получили две точки: . Эти точки принадлежат двум противоположным сторонам квадрата, параллельным прямой EF. Тогда уравнения этих сторон будут иметь вид:

0

Получили уравнения сторон:

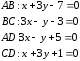
31—40. Построить на плоскости область решений системы линейных неравенств.

40.

при х=0 y=-6, а при y=2 x=2.

при x=-3 y=23, а при x=5 y=14

x=2 => y=2, x=13 => y=5

Решением системы является пересечение решений всех трех неравенств, т.е. треугольник АВС, включая его стороны.

Определим координаты точек треугольника:

50.Составить уравнение линии, каждая точка которой является основанием перпендикуляра, опущенного из начала координат на прямую, проходящую через точку A(2,0).

Обозначим произвольную точку искомой линии . Тогда координаты вектора нормали к прямой проходящей через точку А .

Извините, но дальше не понимаю как решать!!!

11