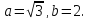Основы векторной алгебры и аналитической геометрии
.docxКонтрольная работа № 1. Основы векторной алгебры и аналитической геометрии
Вариант 7
Задача 1.
Даны
четыре вектора
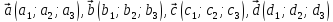 ,
и, заданные в прямоугольной декартовой
системе координат. Требуется: 1) вычислить
скалярное произведение
,
и, заданные в прямоугольной декартовой
системе координат. Требуется: 1) вычислить
скалярное произведение
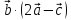 ;
2) вычислить векторное
произведение
;
2) вычислить векторное
произведение
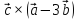 ;
3) показать, что векторы
;
3) показать, что векторы
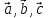 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
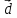 в этом базисе.
в этом базисе.
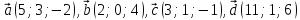
Решение
-
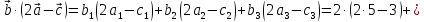
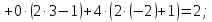
-
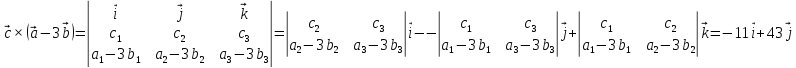 +10
+10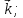
-
Чтобы показать, что векторы
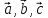 образуют базис необходимо показать,
что
образуют базис необходимо показать,
что

Для этого решим систему:
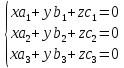
Покажем, что данная система имеет только тривиальное решение. Найдем определитель основной матрицы системы:

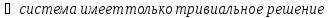 .
.
Найдем
теперь координаты вектора
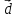 в базисе
в базисе
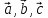 .
Для этого решим систему:
.
Для этого решим систему:

Воспользуемся методом Гаусса:

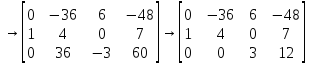
Из
последнего нетрудно видеть, что
 .
Значит, координаты вектора
.
Значит, координаты вектора
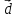 в базисе
в базисе
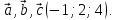
Задача 2.
Даны
координаты вершин пирамиды
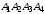 .
Найти: 1) длину ребра
.
Найти: 1) длину ребра
 ;
2) уравнение прямой
;
2) уравнение прямой
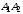 ;
3) угол между рёбрами
;
3) угол между рёбрами
 и
и
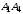 ;
4) уравнение плоскости
;
4) уравнение плоскости
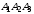 ;
5) угол между ребром
;
5) угол между ребром
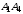 и гранью
и гранью
 ;
6) уравнение высоты,
опущенной из вершины
;
6) уравнение высоты,
опущенной из вершины
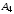 на грань
на грань
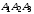 ;
7) площадь грани
;
7) площадь грани
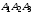 ;
8) объём пирамиды;
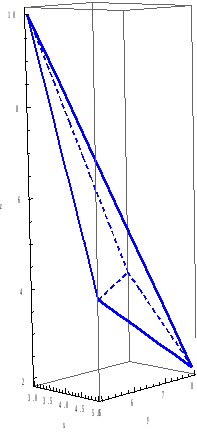
9) сделать чертёж.
;
8) объём пирамиды;
9) сделать чертёж.
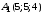 ;
; 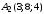 ;
; 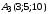 ;
;  .
.
Решение
-
Длина ребра
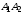 численно равна расстоянию между точками
численно равна расстоянию между точками
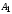 и
и
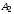 ,
которое в прямоугольной декартовой
системе координат вычисляется по
формуле
,
которое в прямоугольной декартовой
системе координат вычисляется по
формуле
 ,
,
где
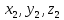 координаты точки
координаты точки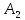 ,
,
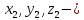 координаты
точки
координаты
точки .
.
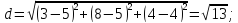
-
Для составления уравнений прямой
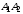 воспользуемся формулой:
воспользуемся формулой:
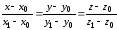 ,
где
,
где
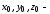 координаты точки
координаты точки
 ,
,
 координаты точки
координаты точки
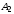 .
Тогда уравнение прямой
.
Тогда уравнение прямой
 имеет вид
имеет вид
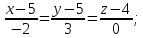
-
Угол
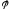 между ребрами
между ребрами
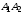 и
и
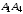 вычисляется по формуле
вычисляется по формуле
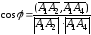 ,
где
,
где
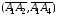 – скалярное произведения векторов
– скалярное произведения векторов
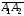 и
и
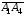 .
.

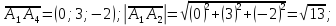
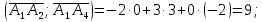
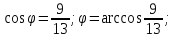
-
Для составления уравнения плоскости
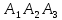 воспользуемся формулой
воспользуемся формулой
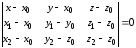
где
 координаты точки
координаты точки ,
,
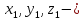 координаты точки
координаты точки
 ,
,
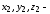 координаты точки
координаты точки
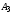 .
.

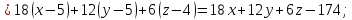
Уравнение
плоскости
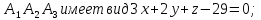
-
Угол
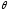 между ребром
между ребром
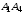 и плоскостью
и плоскостью
 определяется по формуле
определяется по формуле
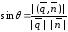 ,
,
где
 – направляющий вектор прямой
– направляющий вектор прямой
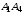 ,
то есть
,
то есть
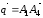 ,
а
,
а
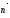 – нормальный вектор плоскости
– нормальный вектор плоскости
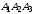 .
.
Из пункта
3
 Из пункта 4
Из пункта 4
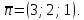
Тогда
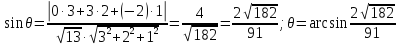
-
Искомое уравнение высоты получим из канонических уравнений прямой
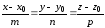 ,
где
,
где
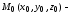 точка, лежащая на искомой прямой;
точка, лежащая на искомой прямой;
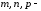 координаты направляющего вектора
координаты направляющего вектора
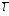 ,
параллельного искомой прямой. При этом
в качестве точки
,
параллельного искомой прямой. При этом
в качестве точки
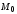 возьмем точку
возьмем точку
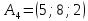 ,
из которой по условию задачи должна
быть опущена высота на плоскость
,
из которой по условию задачи должна
быть опущена высота на плоскость
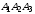 ,
а в качестве вектора
,
а в качестве вектора
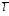 возьмем нормальный вектор плоскости
возьмем нормальный вектор плоскости
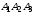 ,
т.е
,
т.е
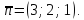 Имеем
Имеем
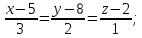
-
Площадь грани
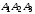 находим, используя геометрический
смысл векторного произведения:
находим, используя геометрический
смысл векторного произведения:
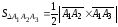 .
.
Находим
векторное произведение векторов
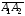 и
и
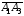 :
:

Т.о.

-
Объем пирамиды
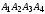 численно равен одной шестой модуля
смешанного произведения векторов
численно равен одной шестой модуля
смешанного произведения векторов
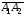 ,
,
 ,
,
 ,
которое находится по формуле
,
которое находится по формуле
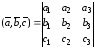 .
.
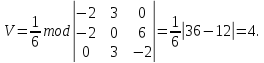
Задача 3.
Найти
координаты точки
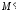 ,
симметричной точке
,
симметричной точке
 относительно прямой
относительно прямой
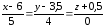 .
.
Решение
Составим
уравнение плоскости Р, проходящей через
точку перпендикулярно прямой L, т.е.
нормальный вектор Р есть

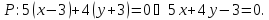
Теперь найдем центр симметрии – точку пересечения прямой L и плоскости Р. Для этого запишем уравнение прямой L в параметрическом виде:

Подставим эти уравнения в общее уравнение плоскости Р и получим:
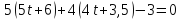
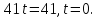
Подставив
полученное значение параметра
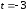 в параметрические уравнения прямой L,
получим координаты точки
в параметрические уравнения прямой L,
получим координаты точки
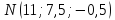 –
точки пересечения прямой L
с плоскостью Р. Но так как N
– середина отрезка
–
точки пересечения прямой L
с плоскостью Р. Но так как N
– середина отрезка
 ,
то
,
то
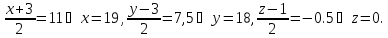
Таким
образом, точка М
имеет координаты
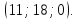
Задача 4.
Составить
уравнение линии, для каждой точки которой
расстояние до точки
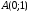 вдвое меньше расстояния до прямой
вдвое меньше расстояния до прямой
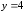 .
Привести полученное уравнение к
каноническому виду и указать тип линии,
описываемой этим уравнением.
.
Привести полученное уравнение к
каноническому виду и указать тип линии,
описываемой этим уравнением.
Решение
Обозначим
произвольную точку искомой линии как
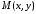 .
Найдем расстояния от точки
.
Найдем расстояния от точки
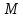 до прямой
до прямой
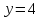 и до точки
и до точки
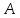 :
:
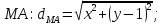

По
условию
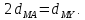 Отсюда имеем:
Отсюда имеем:
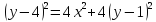
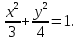
Это
каноническое уравнение эллипса с центром
в начале координат и полуосями