Контрольная работа2

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра программного обеспечения информационных технологий

Факультет ФНиДО

Специальность ПОИТ

Контрольная работа № 2

по дисциплине «ВЫСШАЯ МАТЕМАТИКА»

часть 1

Вариант № 6

Выполнил студент: Бондаренко С.В.

группа 191001

Зачетная книжка № 191001-6

Минск 2011

Основы линейной алгебры

46. Доказать совместность данной системы линейных уравнений и решить её тремя методами: 1) по формулам Крамера; 2) методом Гаусса; 3) средствами матричного исчисления (с помощью обратной матрицы).

Решение: Для определения совместности системы найдем определитель матрицы

Определитель не равен нулю, следовательно система уравнений является совместной.

1) Решим систему уравнений методом Крамера:

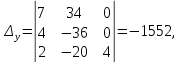
В результате получаем:

2) Решим систему уравнений методом Гаусса:

Умножим второе и третье уравнения на и соответственно, а затем вычтем из первого. Получаем:

В результате:

3) Решим систему уравнений средствами матричного исчисления (с помощью обратной матрицы):

Матрицу решений системы уравнений можно определить по формуле

Здесь – матрица свободных членов.

Обратная матрица определяется по формуле

где – определитель матрицы, - союзная матрица, состоящая из алгебраических дополнений к элементам матрицы А.

56. Найти общее решение системы линейных уравнений.

Решение: Запишем матрицу системы и преобразуем ее к треугольному виду:

Полагаем тогда:

В результате, получаем общее решение системы уравнений

66. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей:

Решение: Составляем характеристическое уравнение и находим его решение:

Решая полученное уравнение, находим собственные значения:

Найдем собственные вектора:

Собственные вектора:

76. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка и построить её в декартовой системе координат:

Решение: Cоставим характеристическое уравнение:

Таким образом, можно записать:

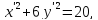
Полученное уравнение является уравнением эллипса.