
Контрольная № 2
.docЗадача 44:

Доказать совместность данной системы линейных уравнений и решить её тремя методами: 1) по формулам Крамера; 2) методом Гаусса; 3) средствами матричного исчисления (с помощью обратной матрицы).
Решение:
1) Решить систему уравнений по формулам Крамера:
Составим матрицу коэффициентов (основную матрицу системы) и найдём её определитель:

Так как определитель отличен от нуля, то система совместна и имеет единственное решение. Вычисляем определители
 ,
,
 ,
,
 ,
которые составляем из матрицы коэффициентов
путём поочерёдной замены каждого из
столбцов на столбец правой части системы.
,
которые составляем из матрицы коэффициентов
путём поочерёдной замены каждого из
столбцов на столбец правой части системы.
Далее по формулам Крамера вычисляем:
![]()
![]() ;
;
![]() .
.
Таким образом, система имеет единственное решение x1 = -4, x2 = -2, x3 = 2.
2) При решении системы линейных уравнений методом Гаусса действия производятся над расширенной матрицей. Запишем матрицу коэффициентов системы А и расширенную матрицу системы В:

Вертикальной чертой мы отделили элементы матрицы системы от свободных членов системы. Определим ранги матрицы А и В.
Для этого проведём преобразования матрицы В:
-
Отнимем от элементов второй строки элементы третьей строки,
-
Первую строку умножим на (-1) и прибавим третью строку;
-
Вторую строку сложим с первой строкой, умноженной на (-2);
Третью строку сложим с первой строкой, умноженной на (-3);
-
Третью строку умножаем на 3, прибавляем к ней вторую.

Отсюда следует, что r(В)=3, минор третьего порядка матрицы А

Следовательно, r(B) = r(A) = 3, т.е. данная система совместна.
Но последняя преобразованная матрица В
 -
это расширенная матрица системы
-
это расширенная матрица системы .
.
"Обратным ходом" метода Гаусса из последнего уравнения системы находим х3 = 2; из второго х2 = – 2; из первого х1 = – 4.
Ответ:

3) Решение матричным методом:
Прежде всего, найдём матрицу А-1, обратную матрице А.
Определитель основной матрицы системы:
 .
.
Алгебраические дополнения всех элементов:

Отсюда

Тогда
Х
=
![]() =
=

 ,
и, следовательно х1=-4;
х2=-2;
х3=2.
,
и, следовательно х1=-4;
х2=-2;
х3=2.
Задача 54:

Найти общее решение системы линейных уравнений.
Решение:
Для исследования совместности применим критерий Кронекера-Капелли. Для этого составим расширенную матрицу системы для определения её ранга и ранга матрицы коэффициентов:
|
|
|
|
Применяя к расширенной матрице, последовательность элементарных операций стремимся, чтобы каждая строка, кроме, быть может, первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей.
|
Вычтем из строки 2 строку 1 умноженную на a2,1= |
2 |
Вычитаемая строка :
|
|
|
|
Модифицированная матрица :
|
|
Вычтем из строки 3 строку 1 умноженную на a3,1= |
3 |
Вычитаемая строка :
|
|
|
|
Модифицированная матрица :
|
|
Вычтем из строки 3 строку 2 умноженную на a3,2= |
1 |
Вычитаемая строка :
|
|
|
|
Модифицированная матрица :
|
Заданная система уравнений не имеет решений (противоречива) т.к. 3-я строка приводит нас к уравнению:
|
0 = |
1 |
что невозможно.
Задача 64:
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.

Решение:
Пусть
 есть столбец координат неизвестного
собственного вектора, принадлежащего
собственному значению
есть столбец координат неизвестного
собственного вектора, принадлежащего
собственному значению
![]() .
.
![]() ,
т.е.
,
т.е.
 (1).
(1).
Эта
система имеет ненулевые решения только
при условии равенства нулю её определителя
![]() .
.
Составим характеристическое уравнение.
 =
=
 =
=
![]() ;
;
Решим
уравнение
![]() .
Откуда получим:
.
Откуда получим:
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() – собственные значение матрицы.
– собственные значение матрицы.
При
![]() система 1 примет вид.
система 1 примет вид.
 ,
,


Собственный
является любой вектор вида:
![]() ,
,
![]() .
.
При
![]() система 1 примет вид.
система 1 примет вид.
 ,
,


Собственный
является любой вектор вида:
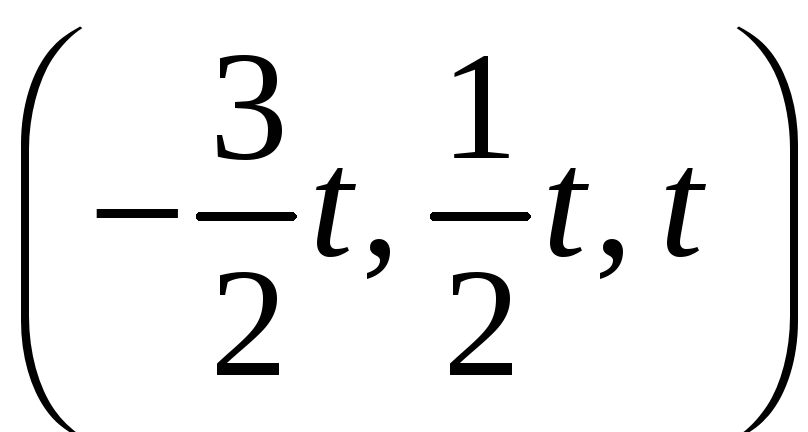 ,
,
![]() .
.
При
![]() система 1 примет вид.
система 1 примет вид.
 ,
,


Собственный
является любой вектор вида:
![]() ,
,
![]() .
.
Задача 74:![]() .
.
Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка и построить её в декартовой системе координат.
Решение.
Матрица квадратичной части многочлена второй степени равна
 .
.
Собственными числами данной матрицы будут
 .
.
Решим
уравнение
![]() =0
получим:
=0
получим:
![]() ,
,
![]() .
.
Вид квадратичной формы:
4x21
Исходное уравнение определяет параболу (λ2 = 0)
Находим главные оси квадратичной формы, то есть собственные векторы матрицы B.
λ1 = 4
-2x1-2y1 = 0
-2x1-2y1 = 0
или
-2x1-2y1 = 0
Собственный вектор, отвечающий числу λ1 = 4 при x1 = 1:
В качестве единичного собственного вектора принимаем вектор:
или
Координаты второго собственного вектора, соответствующего второму собственному числу λ2 = 0, находим из системы:
2x1-2y1 = 0
-2x1 + 2y1 = 0
или
2x1-2y1 = 0
или
Итак, имеем новый ортонормированный базис (i1, j1).
Переходим к новому базису:
или
Вносим выражения x и y в исходное уравнение 2x2 - 4xy + 2y2 - 8x + 8y + 1 и, после преобразований, получаем:

