
курс 1, КОНТРОЛЬНАЯ 1, Вариант № 5
.docУЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
БЕЛАРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Факультет заочного и дистанционного обучения
Специальность: Программное обеспечение информационных технологий
КОНТРОЛЬНАЯ РАБОТА
ПО ВЫСШЕЙ МАТЕМАТИКЕ № 1
Вариант № 5
ФИО
Группа
Зачетная книжка:
Электронный адрес:
Задача 5:
Даны четыре вектора
![]() ,
,
![]() ,
,
![]() и
и
![]() ,
заданные в декартовой системе координат.
Требуется: 1) вычислить скалярное
произведение
,
заданные в декартовой системе координат.
Требуется: 1) вычислить скалярное
произведение
![]() ;
2) вычислить векторное произведение
;
2) вычислить векторное произведение
![]() ;
3) показать, что векторы
;
3) показать, что векторы
![]() образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
![]() в этом базисе.
в этом базисе.
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
1) Найдем вектор
![]()
Так как скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат, то
![]()
2) По аналогии с
пунктом 1 найдем вектор
![]() .
Тогда векторное произведение
.
Тогда векторное произведение
![]() найдем по формуле
найдем по формуле

3) Базисом в
пространстве
![]() являются любые три некомпланарных
вектора. Условием компланарности трех
векторов, заданных в декартовой системе
координат, является равенство их
смешанного произведения нулю. Отсюда
находим:
являются любые три некомпланарных
вектора. Условием компланарности трех
векторов, заданных в декартовой системе
координат, является равенство их
смешанного произведения нулю. Отсюда
находим:
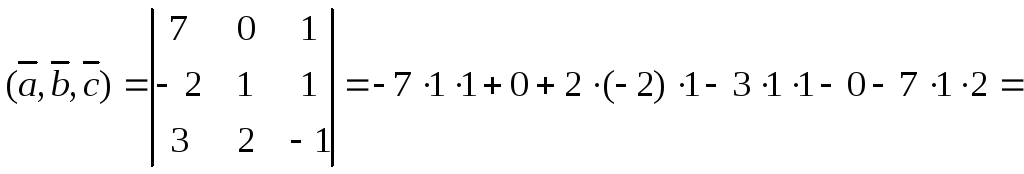
![]()
Значит, векторы
![]() некомпланарны и образуют базис. Составим
систему уравнений в координатном виде
некомпланарны и образуют базис. Составим
систему уравнений в координатном виде
 ,
где
,
где
![]() координаты вектора
координаты вектора
![]() в базисе
в базисе
![]()



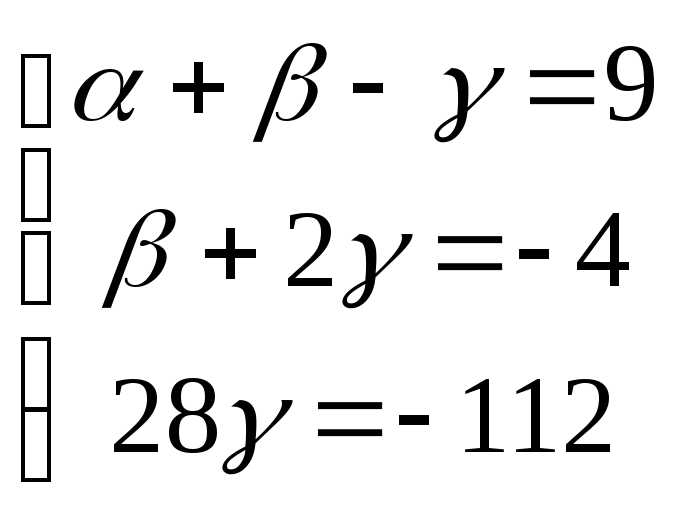

Значит,
![]() .
.
Задача 15: Даны
координаты вершин пирамиды
![]() .
Найти: 1) длину ребра
.
Найти: 1) длину ребра
![]() ;
2) уравнение прямой
;
2) уравнение прямой
![]() ;
3) угол между рёбрами
;
3) угол между рёбрами
![]() и
и
![]() ;
4) уравнение плоскости
;
4) уравнение плоскости
![]() ;
5) угол между ребром
;
5) угол между ребром
![]() и гранью
и гранью
![]() ;
6) уравнение высоты, опущенной из
вершины
;
6) уравнение высоты, опущенной из
вершины
![]() на грань
на грань
![]() ;
7) площадь грани
;
7) площадь грани
![]() ;
8) объём пирамиды; 9) сделать чертёж.
;
8) объём пирамиды; 9) сделать чертёж.
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
1) Длина ребра
![]() численно равна расстоянию между точками
численно равна расстоянию между точками
![]() и
и
![]() ,
которое в декартовой системе координат
вычисляется по формуле
,
которое в декартовой системе координат
вычисляется по формуле
![]() ,
,
где
![]() координаты точки
координаты точки
![]() ,
,
![]() координаты точки
координаты точки
![]() .
.
Таким образом, вычисляем:
![]() .
.
2) Для составления
уравнений прямой
![]() воспользуемся формулой:
воспользуемся формулой:
![]() ,
где
,
где
![]() координаты точки
координаты точки
![]() ,
,
![]() координаты точки
координаты точки
![]() .
Тогда
.
Тогда
![]() ;
;
![]() .
.
3) Угол
между ребрами
![]() и
и
![]() вычисляется по формуле
вычисляется по формуле
![]() из скалярного произведения векторов
из скалярного произведения векторов
![]() и
и
![]() .
.
Находим:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Поэтому
![]() ,
,
![]() .
.
4) Для составления
уравнения плоскости
![]() воспользуемся формулой
воспользуемся формулой
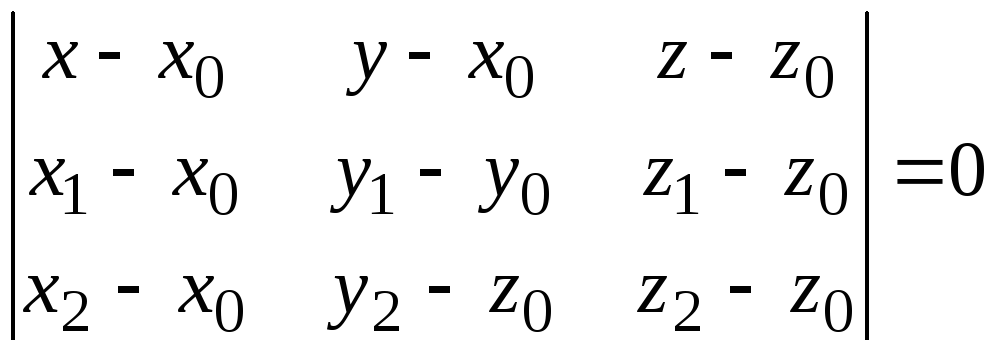 ,
где
,
где
![]() координаты точки
координаты точки
![]() ,
,
![]() координаты точки
координаты точки
![]() ,
,
![]() координаты точки
координаты точки
![]() .
.

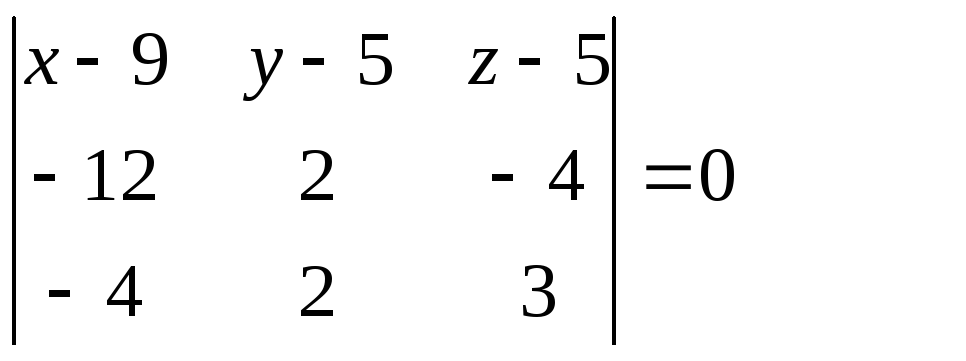
![]()
![]()
![]()
5) Найдем векторное
произведение векторов
![]() и
и
![]()

![]()
![]() .
.
Отсюда
получаем, что
![]()
6) Искомое уравнение
высоты получим из канонических уравнений
прямой
![]() ,
где
,
где
![]() точка, лежащая на искомой прямой;
точка, лежащая на искомой прямой;
![]() координаты вектора
координаты вектора
![]() ,
параллельного искомой прямой. При этом
в качестве точки
,
параллельного искомой прямой. При этом
в качестве точки
![]() возьмем точку
возьмем точку
![]() ,
а
,
а
![]() .
Имеем
.
Имеем
![]() .
.
7) Площадь грани
![]() находим, используя геометрический смысл
векторного произведения:
находим, используя геометрический смысл
векторного произведения:
![]() кв.ед.
кв.ед.
8) Объем пирамиды
![]() численно равен одной шестой модуля
смешанного произведения векторов
численно равен одной шестой модуля
смешанного произведения векторов
![]() ,
,
![]() ,
,
![]() .
.
Таким образом,
 куб.ед.
куб.ед.
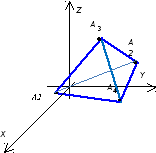
9) Сделаем чертёж:
Задача 25. Найти
координаты точки
![]() ,
симметричной точке
,
симметричной точке
![]() относительно прямой
относительно прямой
![]() .
.
Составим уравнение
плоскости Р, проходящей через точку
![]() перпендикулярно прямой L, т.е.
нормальный вектор Р есть
перпендикулярно прямой L, т.е.
нормальный вектор Р есть
![]() :
:
![]() .
.
Решив совместно уравнения L и Р, получим точку N пересечения L с Р:



![]() .
Но так как N –середина
отрезка
.
Но так как N –середина
отрезка
![]() ,
то
,
то
![]() .
.
Таким образом, точка
![]() имеет координаты
имеет координаты
![]() .
.
Задача 35. Составить
уравнение линии, для каждой точки которой
расстояние до точки
![]() вдвое больше, чем до прямой
вдвое больше, чем до прямой
![]() .
.
Обозначим произвольную
точку искомой линии как
![]() .
.
Расстояние
от М до
прямой
![]() :
:
![]()
Расстояние между
точками АМ:
![]()
Тогда по условию получаем:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Это каноническое уравнение гиперболы.
