
Контрольная работа №2
.docВАРИАНТ №3
Контрольная работа №2
Задание 1,2 – я решал и уверен, что решил неверно.
Задание 3
Даны два линейных преобразования.
Средствами исчисления найти преобразование,
выражающие
![]() через
через
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Решение:
Первое линейное преобразование
 имеет матрицу
имеет матрицу
![]()
![]()
 ,
,
а второе
 имеет
матрицу
имеет
матрицу
 .
.
Тогда произведение линейных преобразований имеет матрицу C=B▪A
C=B▪A=

Поэтому искомое линейное преобразование имеет вид

Задание 4.
Найти собственные значения и собственные векторы матрицы

Решение. Составляем характеристическое уравнение матрицы
Pn(λ)=
 = (-1- λ)((4- λ)(6-
λ)-3▪5)+2(0▪(6- λ)-3▪0)+12(0▪5-(4-
λ)▪0)=
= (-1- λ)((4- λ)(6-
λ)-3▪5)+2(0▪(6- λ)-3▪0)+12(0▪5-(4-
λ)▪0)=
=(-1- λ)(24-4λ-6λ+ λ2-15)=(-1- λ)( λ2-10λ+9)=0
-1- λ=0 λ2-10 λ+9=0
λ1=-1 D=b2-4ac=100-4▪9=64
λ2=![]() =
=
![]() =1
=1
λ3=![]() =
=![]() =9
=9
собственные значения данной матрицы λ1=-1, λ2=1, λ3=9.
Для λ1=-1 система имеет вид
(![]() -1+1)x1-5x2+12x3=0
-1+1)x1-5x2+12x3=0
(4+1)x2+3x3=0
5x2+(6+1)x3=0
-![]() 5x2+12x3=0
5x2+12x3=0
5x2+3x3=0
5x2+7x3=0
Для λ2=-1 система имеет вид
(![]() -1-1)x1-5x2+12x3=0
-1-1)x1-5x2+12x3=0
(4-1)x2+3x3=0
5![]() x2+(6-1)x3=0
x2+(6-1)x3=0
-2x1-5x2+12x3=0
3x2+3x3=0
5x2+5x3=0
x2=-x3
-2x1+5x3+12x3=0
x1=![]() x3
x3
Полагая x3=1 получаем собственный вектор
![]()
Д![]() ля
λ3=9
ля
λ3=9
(-1-9)x1-5x2+12x3=0
(4-9)x2+3x3=0
5![]() x2+(6-9)x3=0
x2+(6-9)x3=0
-10x1-5x2+12x3=0
-5x2+3x3=0
5x2-5x3=0
x2=x3
-10x1-5x3+12x3=0
x1=![]() x3
x3
Полагая x3=1 получая собственный вектор
![]()
Задание 5.
Привести к каноническому виду уравнение
линии второго порядка, используя теорию
квадратичных форм. 6x2+2![]() xy+2y2=21
xy+2y2=21
Решение.
Поскольку в данном случае a11=6
, a12=a21=![]() , a22=2 , то матрица A
этой квадратичной формы
, a22=2 , то матрица A
этой квадратичной формы
A=
![]() ,
,
![]() =0
=0
Решаем характеристическое уравнение
(6-λ)(2-λ)-5=0
12-6λ-2λ+λ2-5=0
λ2-8λ-7=0
Корни λ1=1, λ2=7
Для λ1=1 найдём собственный вектор, составим систему ур-ний
(![]() 6-1)x1+
6-1)x1+![]() x2=0
x2=0
![]() x1+(2-1)x2=0
x1+(2-1)x2=0
5![]() x1+
x1+![]() x2=0
x2=0
![]() x1+x2=0
x1+x2=0
x1=![]()
и для λ2=7
(![]() 6-7)x1+
6-7)x1+![]() x2=0
x2=0
![]() x1+(2-7)x2=0
x1+(2-7)x2=0
-![]() x1+
x1+![]() x2=0
x2=0
![]() x1-5x2=0
x1-5x2=0
x1=![]() x2
x2
Находим собственные векторы :
![]() ;
;
![]() где x2
где x2![]() 0
;
0
;
положив x2=![]() ,
получим
,
получим
![]() ;
;
![]()
нормируем собственные векторы
![]() ,
,
![]()
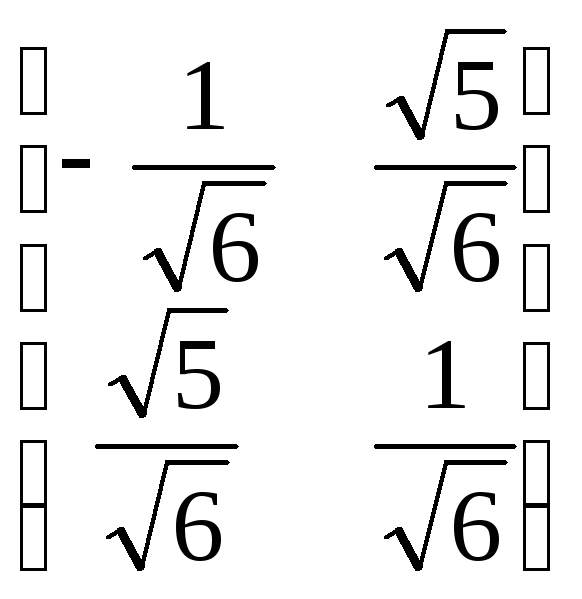
Составляем матрицу перехода от старого базиса к новому
T= ,
в которой координаты нормированных
собственных векторов записаны по
столбцам.
,
в которой координаты нормированных
собственных векторов записаны по
столбцам.
Выполняя преобразования
![]() =
T
=
T![]() =
=
![]()
![]()

![]() +
+![]()
![]()
![]()
![]() x=
x=![]() , y=
, y=
![]()
Значения x и y подставляем в исходное ур-ние и получаем :
![]()
![]()
 это каноническое ур-ние эллипса.
это каноническое ур-ние эллипса.
