Контрольная работа №2

Министерство образования Республики Беларусь

Учреждение образования «Белорусский государственный университет информатики и радиоэлектроники»

Факультет непрерывного и дистанционного обучения

Кафедра высшей математики

Контрольная работа № 2 по дисциплине

Высшая Математика

Вариант работы 8

Выполнил студент группы 00623-028 специальности I-53 01 02 АСОИ дистанционной формы обучения Соболевский Дмитрий Александрович

([e-mail])

Минск 2010

Контрольная работа №2.

Соболевский Д.А АСОИ гр00623-028 Вариант 8

Решение 048

Доказать совместность данной системы линейных уравнений и решить её тремя методами: 1) по формулам Крамера; 2) методом Гаусса; 3) средствами матричного исчисления (с помощью обратной матрицы).

x1 + x2 − x3 =1;

Задача 48: 8x1 + 3x2 − 6x3 = 2;

− 4x1 − x2 + 3x3 = −3.

Решение

Система, имеющая хотя бы одно решение, называется совместной. Необходимым и достаточным условием совместности системы линейных уравнений является

Критерий Кронекера– Капелли. Для того чтобы линейная система была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы. Если же эти ранги не равны, то система несовместна.

(В примере 2 приведено исследование на совместность по критерию Кронекера-Капелли.)

1). Решаем систему уравнений по формулам Крамера:

Составим матрицу коэффициентов (основную матрицу системы) и найдем её

определитель:
		1	1	-1
D =		8	3	-6		= -1¹ 0.
		-4	-1	3

Так как определитель отличен от нуля, то система совместна и имеет единственное решение. Вычисляем определители

	1	1	−1			1	1	−1				1	1	1
1 =	2	3	− 6	= 8 ;	2 =	8	2	− 6	= 4 ;	3 =		8	3	2	= 13 ,
	− 3 −1 3					− 4 − 3 3						− 4 −1 − 3

которые составляем из матрицы коэффициентов путем поочередной замены каждого из столбцов на столбец правой части системы.

Далее по формулам Крамера вычисляем:

x =	1 =	8	= −8; x =		2 =	4	= −4; x =		3 =	13	= −13.
1		−1		2		−1		3		−1
Таким образом, система имеет единственное решение x1									= −8 , x2 = −4 , x3 = −13 .

2). Решаем систему уравнений методом Гаусса:

При решении системы линейных уравнений методом Гаусса действия производятся над расширенной матрицей.

		1	1	− 1		1
~				− 6
Составим расширенную матрицу системы: A =		8	3			2	.
		− 4	− 1	3		− 3

Теперь приведём её путем элементарных преобразований к треугольному или трапециевидному виду. Для этого прибавим ко 2-й строке 1-ю, умноженную на

(−8),		к	3-й	строке прибавим 1-ю, умноженную на (4). Получим:
	1		1	- 1		1
A ~		0	- 5	2		- 6
							. Из 3-й строки вычтем 2-ю умноженную на (0,6) , получим
		0	3	- 1		1

	1 1		−1		1			1 1		−1		1
A ~	0	− 5	2		− 6		~	0	− 5	2		− 6
													.
	0	0	0,2		− 2,6			0	0	1		−13

Таким образом, ранги основной и расширенной матриц равны 3. Система совместна и имеет единственное решение. Она сводится к эквивалентной системе

	x		1	+ x	2	− x	3	= 1;
линейных уравнений		− 5 x 2 + 2 x					3	= −6 ;
								= −13 .
						x
							3

Отсюда, подставляя x3 = −13 во второе уравнение, получим x2 = −4 , а из первого уравнения x1 = − 8 . Итак, x1 = −8 , x2 = −4 , x3 = −13.

3). Решим методами матричного исчисления (с помощью обратной

матрицы):

		1	1	-1
Определитель основной матрицы системы D =		8	3	- 6	= -1 ¹ 0 , значит,
		- 4	-1	3

система совместна и для матрицы коэффициентов существует обратная матрица.

Находим решение по формуле X = A−1B или

												x1									A11				A21					A31
												x				=	1				× A				A					A		× B ,
														2
																	D					12	22							32
												x		3							A				A					A
																						13	23							33
		1
						ij																																	ij		матрицы А:
где B = 2					,	A − алгебраические дополнения элементов a
	− 3
A =				3		− 6		= 3;					A = −								1 −1								= −2;			A =			1 − 1											= −3;
11			− 1			3									21						−1		3									31			3					− 6
																						−1
A = -					8	- 6						= 0; A =								1					= −1;							A = -							1 -1								= -2;
12					- 4	3									22			− 4				3										32							8	- 6
				8		3														1			1										=				1 1						= -5.
A13 =										= 4; A23 = −																	= −3;					A33
			- 4			- 1															− 4	−1															8				3
Таким образом, обратная матрица к основной матрице системы имеет вид
																					3			− 2						− 3
																A−1 = − 0 −1														− 2
																									− 3					.
																					4									− 5

Проверим правильность вычисления обратной матрицы: исходя из определения обратной матрицы, находим

		3	- 2	- 3		1		1	-1		-1 0			0
	−1		-1		×								-1			= E.
A		A = - 0		- 2			8	3	- 6		= -	0		0
			- 3					-1 3				0	0
		4		- 5		- 4								-1

Значит, матричное решение системы имеет вид
x			2	- 2	- 3			1			- 8
1		= -		-1			×			=
x2			0		-14				2		- 4	.
				- 3	- 5
x3			4					- 3			-13
Отсюда следует, что x1	= − 8 ,			x 2 = −4 ,		x 3			= − 13 .

Решение 058

Найти общее решение системы линейных уравнений.

x		- 3x	2	+ x + 2x = 4;
	1			3	4
Задача 58: 2x1 - 5x2 + 4x3 + 3x5 = 7;
x		- 2x	2	+ 3x - 2x		4	+ 3x = 3.
	1			3			5

Решение

Для исследования совместности применим критерий Кронекера-Капелли. Для этого составим расширенную матрицу системы для определения её ранга и ранга матрицы коэффициентов:

		1	− 3	1	2	0		4
[ A |		] = 2 − 5		4 0 3				7
	b
			− 2		− 2
		1		3		3		3

За базисную переменную рекомендуется выбирать ту неизвестную, коэффициент при которой равен единице (во избежание дробных коэффициентов). Оставим без изменения первое уравнение (строку), а за базисную переменную примем x1. Воспользуемся элементарными преобразованиями, а именно: умножим первую строку на (-2) и сложим со второй, затем умножим первую же строку на (- 1) и сложим с третьей. Тогда x1 останется только в первом уравнении (строке):

				−3 1 2 0						−3 1 2 0					4					−3 1		2 0		4
			1				4		1										1
			2 −5		4 0 3		7	−2I ~	0			−4			−1				0		2 −4 3			−1
[A| b] ~										1	2		3					~		1
			1 −2 3 −2 3				3	−I	0	1	2	−4	3		−1		−II		0	0	0	0 0		0

Находим ранг r расширенной матрицы:

Отсюда r[ A | b] = r( A) = 2 .

Таким образом, в данной системе линейных уравнений 2 зависимых и n −r = 3 независимая переменные. Перенося слагаемые с х3,х4,х5 в правую часть (базисный минор образован коэффициентами при х1, х2 ), по последней матрице записываем систему:

x −3x + x +2x = 4;				x	= 4 +3x − x −2x ;
1	2 3	4		1	2 3	4
x2 +2x3 −4x4 +3x5 = −1;				x2	= −1−2x3 +4x4 −3x5 ;

x	=1−7x +10x −9x ;
1	3	4	5
x2	= −1−2x3 +4x4 −3x5 ;

Итак, общее решение неоднородной системы линейных уравнений.

В результате получаем систему с базисными переменными x1, x2 , x3 :

	x			1
		1			−1
	x2
	= x			=
x
		3
	x4
	x5

−7x3	10x4	−9x5				1			−7		10				−9
− 2x3		−3x5
	4x4					−1			− 2		4				−3
x3				=
						0		+ x3	1		+ x4	0		+ x5	0	,
	x4				0			0			1				0
						0			0			0			1
		x5

x3 R;x4 R;x5 R.

Частное решение, в котором все свободные переменные равны нулю, называют базисным решением:

x 3	=	0	x 1 − 3 x 2				= 4			x 1	= 1
x 4	= 0					− 5 x 2	=	7
			2 x		1					2 =	− 1
x 5	=	0		x 1		− 2 x 2	=	3	x

Решение 068
Задача 68
Найти собственные значения и собственные	векторы		линейного
−1		− 7	− 5
	−1	−1
преобразования, заданного в некотором базисе матрицей.			−1 .
	1	5	5

Решение

Составляем характеристическое уравнение матрицы А и находим его корни:

(−1 − λ )

− 7

− 5

| A − λE |=

− 1

(−1 − λ )

− 1

= λ3 − 3λ2 − 6λ + 8 = 0

1

5

(5 − λ )

λ3 − 3λ2

− 6λ + 8 = 0 (λ − 4)(λ2

+ λ − 2) = 0 λ

= 1; λ

2

= −2; λ

3

= 4.

1

+ bx + c = 0 x = − b ±

Так как

ax 2

D ; D = b 2

− 4 ac .

2 a

x 2 + x - 2 = 0 Û x = - 1 ± 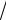9 ; D = 12 - 4 × (-2) = 9. 2

Так как все корни оказались действительными числами, то они являются собственными значениями матрицы А.

При λ = 1 система ( A − λE)x = 0 имеет вид:

− 2x1 −7x2 −5x3 = 0;						−2x −7x −5x = 0;
								1	2	3
							= −2x2		− x3 ;
− x1 − 2x2 − x3 = 0;						x1
		+5x2	+ 4x3 = 0;						+5x2	+ 4x3 = 0;
x1						−2x2 − x3
− 2x − 7x − 5x = 0;						− 2x1 − 7x2 − 5x3					= 0;	x1		= x3 ;
		1	2	3
	x = −2x − x ;					x = −2x − x ;
	1		2	3		1		2	3					= −x .
3x + 3x = 0;						3x + 3x = 0;						x
													2	3
		2	3				2	3

Значит, собственному значению λ1 = 1 соответствует собственный вектор

	x	1			x	3				1
					− x3			= x3
x1	= x	2		=						− 1
					x3					1
	x3

Здесь х3 – произвольное действительное число, не равное нулю. Положив его,

=(1

−1 1)T .

в частности, равным единице, получим собственный вектор в виде

x

1

Аналогично при λ = −2 система ( A − λE)

=

имеет вид:

x

0

x1 −7x2 −5x3 =0;

x −7x

2

−5x = 0;

x −7x

2

−5x = 0;

−x + x −x =0;

1

3

1

3

x1

= 2x2 ;

x = x

2

− x ;

1

2

3

x1 = x2 − x3 ;

1

3

x

= −x .

x +5x +7x =0;

x

− x +5x

+7x = 0;

x = −x ;

2

2

3

2

1

2

3

3

3

2

3

Значит, собственному значению λ2 = −2 соответствует собственный вектор

x1

2 x

2

2

x 2 = x

2

=

x 2

=

x 2 1 .

− 1

x

3

− x 2

Здесь

х2

–

произвольное

действительное

число,

не

равное

нулю.

Соответствующий собственный вектор имеет вид

= (2

1 −1)T .

x2

Аналогично при λ = 4 система ( A − λE)

=

имеет вид:

x

0

−5x −7x −5x =0;

−5x −7x −5x =0;

1

2

3

1

2

3

−x1

−5x2 −x3 =0;

−x1 −5x2 +x1 +5x2 =0;

+ x3 =0;

=−x1 −5x2;

x1 +5x2

x3

−5x1 −7x2 +5x1 +25x2 = 0;

x2

=0;

−5x2 − x3 = 0;

− x1

=−x1 ;

x =− x −5x ;

x3

3

1

2

Значит, собственному значению λ3

= 4 соответствует собственный вектор

x1

x1

1

x3 =

= x1

x2

= 0

0 .

− x1

x3

−1

=1, получим собственный вектор в виде

= (1

1

1)T .

Приняв x

x

1

3

Таким образом,

матрица А имеет три собственных значения λ1 =1,

λ2 = −2 ,

λ3

= 4 , а нормированные собственные векторы имеют вид

1

1 1

T

2

1

1 T

1

1 T

x =

0 −

x =

−

x =

−

1

2

6

3

2

2

3

3 3

6

6

Решение 078 Задача 78

Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка и построить её в декартовой системе координат: x2 + y2 − 4xy + 4x − 2 y +1 = 0 .

Решение

Составим матрицу данной квадратичной формы	1		− 2	и найдём её
	A =
		− 2
			1

собственные значения:

| A −λE |=		1−λ	−2				= (1				−λ)2								−4 = (1−λ −2)(1−λ +2) = (λ +1)(λ −3) = 0.
		−2	1−λ
Корнями характеристического уравнения являются числа λ1 = −1 и λ2 = 3 .
Им соответствуют собственные векторы																																			=(1 1)T																		=(−1 1)T .
																													u																и u
																											1																								2
Нормируя собственные векторы, получим
											1								1						T																				1								1						T
			a1				=																					и a								2 =					−																		.
											2								2																										2								2
Матрица перехода Т к новому базису имеет вид
																											1									1
																T =											2									2
																																										.
																								−			1									1
																											2									2
Вводим замену переменных
								1						′					1						′																1							′						1					′
			x =												+																					= −															+
							2					x							2						y ;							y									2					x							2						y .

Подставим эти выражения в исходное уравнение кривой:

1					1				2						1								1				2		1										1							1					1
				x′+				y′	+			−							x′+							y′		− 4								x′+							y′		−					x′+				y′	+
		2				2									2								2									2							2							2						2
										1							1												1								1
								+ 4						x′ +									y′			+ 2		−					x′ +								y′			+1		= 0 .
										2							2												2										2
После преобразования выражения получим

						3 x′2							x′			y′2		+		2						+ 1 = 0
								+			6	2		−									2 y ′						,
				2							2
													2									2
	(y′−			−	3(x′+						= −1				3(x′+								−	( y′−
		2)2					2)2												2)2								2)2		=1
или
	2			2													2					2

Введя замену y′′ = y′−2 , x′′= x′+2 , получим уравнение гиперболы

3	( x ′′ ) 2 −	1	( y ′′ ) 2 = 1
2
	2

в системе координат X ′′Y ′′ . График полученной гиперболы приведен на следующем рисунке.

	Y	Y
Y'		X' X

O = O' O

X