
К.р. №1. 9 вариант
.docxЗадача 9.
Даны
четыре вектора
 ,
,
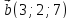 ,
,
 ,
,
 в векторном базисе. Показать, что векторы
в векторном базисе. Показать, что векторы
 ,
,
 ,
,
 образуют базис, и найти координаты
вектора
образуют базис, и найти координаты
вектора
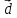 в этом базисе.
в этом базисе.
Вычисляем:


Следовательно,
векторы
 ,
,
 ,
,
 образуют базис, и вектор
образуют базис, и вектор
 линейно выражается через базисные
векторы:
линейно выражается через базисные
векторы:

Или в координатной форме:

Решим полученную систему при помощи формул Крамера:
 =
=







 ;
;
 ;
;

Поэтому

Ответ:

Задача 19.
Даны координаты вершин пирамиды A1A2A3A4. Найти: 1) длину ребра A1A2; 2) угол между ребрами A1A2 и A1A4; 3) угол между ребром A1A4 и гранью A1A2A3; 4) площадь грани A1A2A3; 5) объем пирамиды; 6) уравнение прямой A1A2; 7) уравнение плоскости A1A2A3; 8) уравнение высоты, опущенной из вершины A4 на грань A1A2A3. Сделать чертеж.
Координаты вершин пирамиды: A1 (7; 5; 3), A2 (9; 4; 4), A3 (4; 5; 7), A4 (7; 9; 6).
1) Длину ребра A1A2 находим по формуле расстояния между двумя точками:


2)
Угол между ребрами A1A2
и A1A4
найдем как угол между векторами
 и
и


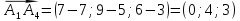
Косинус угла между векторами


3)
Угол между ребром и гранью определим
вычислив координаты нормального вектора
плоскости A1A2A3.
Он будет равен векторному произведению
векторов
 и
и

 ;
;

Векторное произведение

Нормальный
вектор

Синус угла

Угол
равен

4)
Площадь грани A1A2A3
равна половине векторного произведения


5)
Объем пирамиды равен шестой части
смешанного произведения векторов
 ,
,
 ,
,
 .
.
 ;
;
 ;
;

Смешанное произведение:

Объем пирамиды:

6) Уравнение прямой A1A2
Направляющим
вектором прямой является
 ,
кроме того прямая проходит через точку
A1
(7; 5; 3).
,
кроме того прямая проходит через точку
A1
(7; 5; 3).
Уравнение прямой:

7) Уравнение плоскости A1A2A3
Нормальный
вектор плоскости
 ,
кроме того плоскость проходит через
точку A1
(7; 5; 3).
,
кроме того плоскость проходит через
точку A1
(7; 5; 3).
Уравнение плоскости:


 -
уравнение
плоскости A1A2A3.
-
уравнение
плоскости A1A2A3.
8) Уравнение высоты, опущенной из вершины A4 на грань A1A2A3
Нормальный вектор A1A2A3 является направляющим вектором искомой высоты, кроме того высота проходит через точку A4 (7; 9; 6).
Уравнение высоты, опущенной из вершины A4 на грань A1A2A3:

Чертеж:

Задача 29.
Составить уравнение линии, каждая точка которой отстоит от точки A(4; 0) вдвое дальше, чем от прямой x=1.
Пусть искомой линии принадлежит точка M(x; y).
Тогда
расстояние от точки M
до точки A(4;
0) будет

Расстояние
от точки M
до прямой x=1

По
условию
 откуда
получим уравнение
откуда
получим уравнение

После преобразований получим
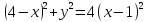



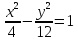
Ответ:

Задача 39.
Доказать совместность данной системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления:

Совместность матрицы докажем по теореме Кронекера-Капелли.
Найдем ранг матрицы данной системы А и ранг расширенной матрицы В.
 ;
;

Из второй строки вычитаем первую умноженную на 2 и из третьей строки вычитаем первую умноженную на 3. Затем вычтем из третьей строки вторую, умноженную на 4/7.

Следовательно
 ,
значит исходная система совместна и
имеет единственное решение.
,
значит исходная система совместна и
имеет единственное решение.
1) решим систему методом Гаусса.
Составим систему

Результат
 ,
,
 ,
,
 .
.
2) решим систему средствами матричного исчисления.
Решение
средствами матричного исчисления имеет
вид
 .
.
Сначала найдем обратную матрицу:

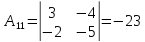 ;
;
 ;
;

 ;
;
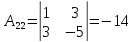 ;
;
 ;
;
 ;
;
 ;
;
 .
.


Следовательно,
 ,
,
 ,
,
 .
.
Ответ:
 ,
,
 ,
,
 .
.
Задача 49.
Найти размерность и базис пространства решений однородной системы линейных уравнений.

Сначала найдем ранг матрицы системы путем преобразований:
Поменяем местами первую строку с третьей, затем вычтем из второй строки первую, умноженную на три, и из третьей первую умноженную на семь. Потом вычтем из третьей строки вторую, умноженную на два.

Ранг матрицы равен r=2. Количество неизвестных n=4. Так как ранг системы меньше числа неизвестных, то система имеет ненулевые решения. Размерность пространства решений матрицы равна n-r=4-2=2.
Преобразованная система уравнений:

Эти формулы дают общее решение, т.к. придавая x3 и x4 произвольные значения, получим x1 и x2. Запишем решение в виде вектора-столбца и разложим его по фундаментальной системе решений

Полагаем
x3=C1
и x4=C2
где C1
и C2
произвольные постоянные, получаем общее
решение в виде
 ,
где
,
где

образуют базис пространства решений.
Ответ: размерность пространства решений матрицы равна n-r=2;
базис
пространства решений
 .
.
Задача 59.
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей:

Характеристическое
уравнение матриц имеет вид
 откуда характеристическое уравнение
данной матрицы имеет вид
откуда характеристическое уравнение
данной матрицы имеет вид




Получаем
собственные значения
 ,
,
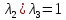 .
.
При
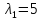 получаем систему
получаем систему

При
x1=1
получаем собственный вектор

При
 получаем систему
получаем систему

При
x3=1
получаем собственные векторы

Ответ:
собственные значения
 ,
,
 ;
;
собственные
векторы
 ,
,
 .
.
Задача 79.
Привести
к каноническому виду уравнение линии
второго порядка, используя теорию
квадратичных форм:
 .
.
Матрица
квадратичной формы
 имеет вид
имеет вид

Решим
характеристическое уравнение :




Собственные
значения матрицы А

Найдем собственные векторы из системы

Для

 ;
; 
Для

 ;
; 
Нормируем
собственные векторы

 ;
; 
Составим матрицу перехода от одного базиса к новому

и выполним преобразование



Из исходного уравнения кривой получим


После
преобразований получим

Приведем уравнение к каноническому виду
 – каноническое
уравнение элипса с полуосями
– каноническое
уравнение элипса с полуосями
 ;
;

Ответ:

