
К.р. №2 3 вариант
.doc
|
Искуственный |
|
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Факультет непрерывного и дистанционного обучения Специальность: Искусственный Интеллект
КОНТРОЛЬНАЯ РАБОТА № 2 ПО ВЫСШЕЙ МАТЕМАТИКЕ Вариант № 8
Ф.И.О. Группа Зачетная книжка Электронный адрес
|
Задание 48
Доказать совместность данной системы линейных уравнений и решить её тремя методами: 1) по формулам Крамера; 2) методом Гаусса; 3) средствами матричного исчисления (с помощью обратной матрицы).

Решение.
1) Система, имеющая хотя бы одно решение, называется совместной. Необходимым и достаточным условием совместности системы линейных уравнений является
Критерий Кронекера–Капелли. Для того чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу её основной матрицы. Если же эти ранги не равны, то система несовместна.
Для этого составим расширенную матрицу системы для определения её ранга и ранга матрицы коэффициентов:

Находим ранг r расширенной матрицы:
-
3-ю строку умножим на 2 и сложим со 2 строкой:

1.2. 1-ю строку умножаем на 4 и складываем с 3-ей строкой:

1.3. умножаем 2-ю строку на (-3) и складываем с 3-ей:

Отсюда r = r![]() = r(A) = 3.
= r(A) = 3.
Таким образом, в данной системе n = 3 линейных уравнений r = 3 зависимых переменных.
2) Решим систему уравнений по формулам Крамера, для этого составим матрицу коэффициентов (основную матрицу системы) и найдем её определитель:
 = 1*3*3+(-1)*8(-1)+1*(-6)*(-4) – (-1)*3*(-4) – 1*8*3 –
1*(-6)*(-1) = -1
= 1*3*3+(-1)*8(-1)+1*(-6)*(-4) – (-1)*3*(-4) – 1*8*3 –
1*(-6)*(-1) = -1![]() 0
0
Так как определитель отличен от нуля, то система совместна и имеет единственное решение. Вычисляем определители, заменяя поочередно столбцы основной матрицы свободными членами.
![]() 1
=
1
=  = 8
= 8
![]() 2
=
2
= 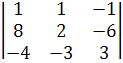 = 4
= 4
![]() 3
=
3
=  = 13
= 13
Далее по формулам Крамера вычисляем:
X1 = ![]() X2 =
X2 = ![]() X3 =
X3 = ![]()
Таким образом, система имеет единственное решение X1 = -8, X2 = -4, X3=-13.
3) Решим систему линейных уравнений методом Гаусса.
3.1. Составим расширенную матрицу системы:
![]() =
= 
3.2. Из пункта 1.3. она равнозначна матрице:
![]() =
= 
3.3.Таким образом, ранги основной и расширенной матриц равны 3. Система совместна и имеет единственное решение. Она сводится к эквивалентной системе линейных уравнений:
X 1
– X2 + X3
= 1
1
– X2 + X3
= 1
X2 = -4
-X3 = 13
Отсюда, подставляя X2 =-4 и X3=-13, в первое уравнение, получим X1 = -8, Итак, X1 =-8, X2 =-4 X3=-13.
4) Решим систему линейных уравнений матричным методом.
4.1. Определитель основной матрицы:
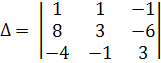 = 1*3*3+(-1)*8(-1)+1*(-6)*(-4)–(-1)*3*(-4)–1*8*3–1*(-6)* *(-1)
= -1
= 1*3*3+(-1)*8(-1)+1*(-6)*(-4)–(-1)*3*(-4)–1*8*3–1*(-6)* *(-1)
= -1![]() 0, значит, система совместна и для матрицы
коэффициентов существует обратная
матрица. Находим решение по формуле
0, значит, система совместна и для матрицы
коэффициентов существует обратная
матрица. Находим решение по формуле
![]() или
или
 ,
,
где
![]() алгебраические дополнения элементов
алгебраические дополнения элементов
![]() матрицы А:
матрицы А:
A = (-1)i+k M,
где М – минор элемента aik
А11
=
![]() =
3*3 – (-6)*(-1)=3;
А21
=
=
3*3 – (-6)*(-1)=3;
А21
=
![]() =-2;
А31
=
=-2;
А31
=
![]() =-3;
=-3;
А12
=
![]() =
0;
А22
=
=
0;
А22
=
![]() =
-1;
А32
=
=
-1;
А32
=
![]() =-2;
=-2;
А13
=
![]() =
4;
А23
=
=
4;
А23
=
![]() =-3;
А33
=
=-3;
А33
=
![]() =
-5.
=
-5.
Таким образом, обратная матрица к основной матрице системы имеет вид.
А-1
= -1
Значит, матричное решение системы имеет вид
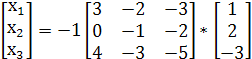
Отсюда следует, что х1 = 3*1 – 2*2 – 3*(-3) = -8
х2 = 0*1 – 1*2 – 2*(-3) =-4
х3 = 4*1 – 3*2 – 5*(-3) =-13
Ответ: х1 = -8; х2 =-4; х3 =-13.
Задание 58
Найти общее решение системы линейных уравнений.

Решение.
Для исследования совместности применим критерий Кронекера-Капелли – для того чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу её основной матрицы. Если же эти ранги не равны, то система несовместна.
Для этого составим расширенную матрицу системы для определения её ранга и ранга матрицы коэффициентов:

1. Найдем ранг r расширенной матрицы:
1.1. Сложим 2-ю строку умноженную на (-1) с 3-ей строкой:

1.2. 1-ю строку сложим с 3-ей строкой:

1.3. 1-ю строку умножим на (-2) и сложим со 2-ой строкой
![]()
1.4. Отсюда
r = r![]() =
r(А) =2
=
r(А) =2
Таким образом, в данной системе n = 5 линейных уравнений r = 2 зависимых и n – r = 3 независимых переменных. Перенося слагаемые с х3, х4, х5 в правую часть (базисный минор образован коэффициентами при х1, х2), по последней матрице записываем систему
х 1
– 3х2 = 4 – х3 – 2х4
1
– 3х2 = 4 – х3 – 2х4
х2 = -1 – 2х3 + 4х4 – 3х5
х 1
=3 – 3х3 +2х4 – 3х5
1
=3 – 3х3 +2х4 – 3х5
х2 = -1 – 2х3 + 4х4 – 3х5
Итак, общее решение неоднородной системы линейных уравнений
 =
= =
= +
+ +
+ ,
,
![]()
Отсюда следует, что вектора ![]() = (-3; -2; 1)Т, (2; 4; 1)Т, (-3; -3; 1)Т
являются решением однородной системы
= (-3; -2; 1)Т, (2; 4; 1)Т, (-3; -3; 1)Т
являются решением однородной системы
![]() ,
а вектор
,
а вектор ![]() = (3; -1; 0; 0; 0)Т есть частное решение
исходной системы
= (3; -1; 0; 0; 0)Т есть частное решение
исходной системы
![]() .
Обозначив произвольные константы х3,
х4, х5 через с, d,
k получим общее решение
системы в виде
.
Обозначив произвольные константы х3,
х4, х5 через с, d,
k получим общее решение
системы в виде![]() +c
+c![]() +d
+d![]()
Ответ: общее решение исходной
системы![]() +c
+c![]() +d
+d![]()
Задание 68
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.
 .
.
Решение.
1) Составляем характеристическое уравнение матрицы А и находим его корни:
![]() =
=  = (-1 –
= (-1 –![]() (-1 –
(-1 – ![]() +
+(-5)*(-1)*5 + (-7)*(-1)*1 – (-5)* (-1 –
+
+(-5)*(-1)*5 + (-7)*(-1)*1 – (-5)* (-1 –![]() - (-7)*(-1)*
- (-7)*(-1)*![]() - (-1 –
- (-1 –![]() *(-1)*5
=
*(-1)*5
=![]() 3
3![]()
2) Найдем корни характеристического уравнения.
![]() 3
3![]() = (
= (![]()
![]()
![]()
Так как все корни оказались действительными числами, то они являются собственными значениями матрицы А.
3) При ![]() система
система
![]() имеет вид:
имеет вид:
х
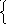 1
– 7х2 – 5х3 = 0 х1
= -2х3
1
– 7х2 – 5х3 = 0 х1
= -2х3
-х1+х2 – х3
= 0 ![]() х2 = -х3
х2 = -х3
х1+5х2+7х3 =0
Значит, собственному значению ![]() соответствует собственный вектор
соответствует собственный вектор
 =
=  =
= ![]() =
=![]()
Здесь х3 – произвольное действительное число, не равное нулю. Положив его, в частности, равным единице, получим собственный вектор в виде
![]() = (-2,-1,1)Т
= (-2,-1,1)Т
4) Аналогично при ![]() система
система
![]() имеет вид:
имеет вид:
-
 5х1
– 7х2 – 5х3 = 0 х1
= -х3
5х1
– 7х2 – 5х3 = 0 х1
= -х3
-х1 – 5х2 –
х3 = 0 ![]() х2 = 0
х2 = 0
х1+5х2+х3 =0
Значит, собственному
значению ![]() соответствует собственный вектор
соответствует собственный вектор
 =
=  =
= ![]() =
=![]()
Здесь х3 – произвольное
действительное число, не равное нулю.
Соответствующий собственный вектор
имеет вид ![]() = (-1,0,1)Т
= (-1,0,1)Т
5)Аналогично при ![]() система
система
![]() имеет вид:
имеет вид:
-
 2х1
– 7х2 – 5х3 = 0 х1
= -х2
2х1
– 7х2 – 5х3 = 0 х1
= -х2
-х1 –2х2 –
х3 = 0 ![]() х3 = -х2
х3 = -х2
х1+5х2+4х3 =0
Значит, собственному
значению ![]() соответствует собственный вектор
соответствует собственный вектор
 =
=  =
= ![]() =
=![]() .
.
Приняв х2 =1, получим собственный
вектор в виде ![]() = (-1,1,-1)Т
= (-1,1,-1)Т
Ответ: матрица А
имеет три собственных значения ![]() ,
,
![]() ,
,
![]() ,
а соответствующие им собственные векторы
имеют вид
,
а соответствующие им собственные векторы
имеют вид ![]() =
= =
= =
=
Задание 78
Используя теорию
квадратичных форм, привести к каноническому
виду уравнение линии второго порядка
и построить её в декартовой системе
координат.
![]() .
.
Решение.
1) В уравнении заданной кривой присутствует
квадратичная форма следующего вида:![]() .
Составим матрицу данной квадратичной
формы А =
.
Составим матрицу данной квадратичной
формы А = ![]() и найдём её собственные значения:
и найдём её собственные значения:
![]() =
=![]() =
(
=
(![]() *(–
2) = (
*(–
2) = (![]() 2
– 4 = (
2
– 4 = (![]() +1)*(
+1)*(![]() – 3) = 0
– 3) = 0
Корнями характеристического уравнения
являются числа
![]() и
и![]() .
Им соответствуют собственные векторы
.
Им соответствуют собственные векторы
![]() =(1;1)Т и
=(1;1)Т и ![]() =(-1;1)Т.
=(-1;1)Т.
2) Нормируем собственные векторы:
 ;
; .
.
Тогда нормируя собственные векторы, получим
![]() = (
= (![]() )Т
и
)Т
и ![]() = (
= (![]() )Т.
)Т.
Тогда
в базисе, ![]() искомое ортогональное преобразование
искомое ортогональное преобразование
![]() ,
приводящее эту КФ к каноническому виду,
имеет матрицу Т.
,
приводящее эту КФ к каноническому виду,
имеет матрицу Т.
Матрица перехода Т к новому базису имеет вид
Т =  .
.
3) В соответствии с соотношением
![]() вводим замену переменных
вводим замену переменных
![]()
4) Подставим эти выражения в исходное уравнение кривой:
![]()
![]() .
.
5) После преобразования выражения получим
![]() ,
,
или
![]() .
.
6)
Введя замену
![]() ,
,
![]() ,
получим уравнение гиперболы
,
получим уравнение гиперболы
3![]()
![]()
![]()
7)
В системе координат
![]() .
График полученной гиперболы приведен
на следующем рисунке.
.
График полученной гиперболы приведен
на следующем рисунке.

 У
У
 X’
y’
X’
y’

 X’’
y’’
X’’
y’’
 Х
Х

Литература
1. Высшая математика. Общий курс /Под общ. ред. С.А.Самаля. Мн.:Вышейш. Шк., 2000.
2. Кузнецов А.В. Сборник задач и упражнений по высшей математике. Общий курс: Учеб. пособие. Мн.:Вышейш. Шк., 1994
3. Минюк С.А., Самаль С.А., Шевченко Л.И. Высшая математика для экономистов. Мн.: ООО «Элайда», 2003.
4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. I, II – М.: Высш. шк., 1980.
