
К.р. №2 20 вариант
.docx
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра программного обеспечения информационных технологий
Факультет ФНиДО
Специальность ПОИТ
Контрольная работа № 2
по дисциплине «Высшая математика»
Вариант № 10
Выполнил студент: Ткаченко Дмитрий
группа 191003
Зачетная книжка 191003-20
Минск 2011
-
Доказать совместность данной системы линейных уравнений и решить ее тремя способами:
а) по формулам Крамера
б) методом Гаусса
в) средствами матричного исчисления

а) ∆= = 4(-10+18)+3(-4+15)+2(12-25)=32+33-26=39≠0
= 4(-10+18)+3(-4+15)+2(12-25)=32+33-26=39≠0
∆1= = 8(-10+18)+3(-22+39)+2(66-65)=64+51+2=117
= 8(-10+18)+3(-22+39)+2(66-65)=64+51+2=117
∆2= = 4(-22+39)-8(-4+15) +2(26-55) =68-88-58=-78
= 4(-22+39)-8(-4+15) +2(26-55) =68-88-58=-78
∆3 = = 4(65-66)+3(26-55)+8(12-25) =-4-87-104=-195
= 4(65-66)+3(26-55)+8(12-25) =-4-87-104=-195
x1= =
= =3;
x2=
=3;
x2= =
=
 = -2; x3 =
= -2; x3 =
 =
=
 = -5
= -5
x1=3; x2=-2; x3=-5
б)
 А=
А=

Для удобства вычислений поменяем строки местами:
Умножим 1-ую строку на (2). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
Умножим 2-ую строку на (5). Умножим 3-ую строку на (-4). Добавим 3-ую строку к 2-ой:
Умножим 1-ую строку на (3). Добавим 2-ую строку к 1-ой:
Из 1-ой строки выражаем x3
Из 2-ой строки выражаем x2
Из 3-ой строки выражаем x1
в) А= B=
B=

 =
=
X= ·
B=
·
B= ·
·
 =
=

Ответ: 3; -2; -5
-
Найти общее решение системы линейных уравнений

Сформируем расширенную матрицу

Применяя к расширенной матрице, последовательность элементарных операций стремимся, чтобы каждая строка, кроме, быть может, первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей.
Вычтем из строки 2 строку 1 умноженную на а2,1=2
Вычитаемая строка

Модифицированная матрица

Вычтем из строки 3 строку 1 у множенную на а3,1=1
Вычитаемая строка

Модифицированная матрица

Вычтем из строки 3 строку 2 у множенную на а3,2=1
Вычитаемая строка

Модифицированная матрица

Заданная система уравнений не имеет решений (противоречива), т.к. 3-я строка приводит нас к уравнению: 0=1, что невозможно.
-
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей

Pn (λ) =

Pn (λ) = - λ3+7 λ-6
- λ3+7 λ-6=0 или λ3-7 λ+6=0
λ3-7 λ+6=( λ-2)( λ-1)( λ+3)=0
λ1=-2; λ2=-1; λ3=3.
(4- λ)x1+7x2+x3=0
-x1+(-4-λ)x2-x3=0
-3x1-x2-(0-λ)x3=0



λ1=-2
(A-λE)X=0
 ~
~

 ~
~

x=
λ2=-1
(A-λE)X=0
 ~
~

 ~
~
x=

λ3=3
(A-λE)X=0
 ~
~
 ~
~


x=
-
Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка и построить её в декартовой системе координат.
3x2+3y2-4xy+4x+4y+1=0
f(x,y)=3x2-4xy+3y2; A=

f1(x’,y’)= λ1x’2+ λ2y’2;
C=
 =
0
=
0
( )2-4=0
)2-4=0
λ2-6λ+5=0
D=(-6)2-4·1·5= =4; λ1,2=
=4; λ1,2=

λ1=1; λ2=5 – корни характеристического уравнения матрицы А
x'2+5y’2+4x’+4y’+1=0
(x’2+2·2x+4)-4+5(y’2+ · 2y+
· 2y+ )
-
)
-
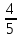 +1=0
+1=0
(x’+2)2+5(y’+ )2
= 4+
)2
= 4+ -1;
-1;
(x’+2)2+5(y’+ )2
=
)2
=
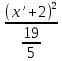 +
+
 = 1 – уравнение эллипса
= 1 – уравнение эллипса
Центр (-2;
 )
)
Малая полуось b
Большая полуось а
a≈1.9
b≈0.25

