Решение
Чтобы построить гистограмму относительных частот, нужно преобразовать на интервальное статистическое распределение относительных частот (эмпирических вероятностей) и найти плотность этих относительных частот. Для этого сначала определим объем выборки и эмпирические вероятности:
n=2+3+5+1+4+2+3=20,
Найдем длину частичных интервалов, частичные интервалы и плотность относительных частот. Частичные интервалы определим из условия, что заданные в дискретном статистическом распределении варианты должны быть серединами частичных интервалов.
Следовательно, длина частичных интевалов:
h = xi+1 - xi =2,
Искомое интервальное статистическое распределение эмпирических вероятностей имеет такой вид:
(хі; хi+1] |
(1;3] |
(3; 5] |
(5; 7] |
(7; 9] |
(9; 11] |
(11; 13] |
(13; 15] |
Wi |
0,1 |
0,15 |
0,25 |
0,05 |
0,2 |
0,1 |
0,15 |
Плотности емпирических вероятностей такие:
Теперь можно легко построить искомую гистограмму относительных частот.
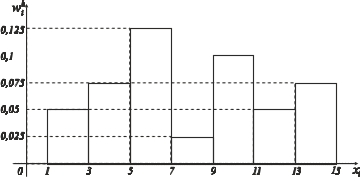
Пример 2. Исследователь, который определяет интенсивность труда рабочих механического цеха в отчетном году в процентах до прошлого года, получил таблицу частот :
Изделия, % |
80-90 |
90-100 |
100-110 |
110-120 |
Количество рабочих я |
1 |
2 |
5 |
2 |
Записать статистическое распределение.
Пусть случайная величина — интенсивность труда одного рабочего. Шаг таблицы частот h = 10, а ширина выборки — 40. Определим середины интервалов : х1 = 85; х2 = 95; х3 = 105; х4 = 115. Вычислим относительные частоты: (w1 = 0,1; w2 = 0,2; w3 = 0,5; w4= 0,2. Следовательно, статистическое распределение имеет вид:
х |
85 |
95 |
105 |
115 |
w |
0,1 |
0,2 |
0,5 |
0,2 |
Числовые характеристики выборки
Среднее
арифметическое значение выборки
называется выборочным средним
и вычисляется по формулам:
,
где xi — значение і-й варианты; ni — частота і-й варианты; n — объем выборки; k — количество вариант в выборке; wi — относительная частота і-й варианты.
Средний квадрат отклонения значений элементов выборки от выборочного среднего называется выборочной дисперсией D и вычисляется по формулам:
После преобразований, формулы, для нахождения выборочной дисперсии несколько упрощаются:
то есть выборочная дисперсия равняется разнице среднего квадрата элементов выборки и квадрата выборочного среднего.
Квадратный корень из выборочной дисперсии
называется средним квадратичным отклонением выборки.
Пример 1. Задано статистическое распределение выборки :
xi |
1 |
3 |
4 |
7 |
10 |
12 |
15 |
ni |
5 |
2 |
12 |
7 |
4 |
3 |
2 |
Найти выборочное среднее, выборочную дисперсию и среднее квадратичне отклонение выборки.