11) Закон распределения дискретной случайной величины(не эскалопский вариант)
Случайной величиной называют переменную величину, которая в зависимости от исходов испытания принимает значения, зависящие от случая. Случайная величина, при ни мающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, называется дискретной случайной величиной. Случайная величина, которая может принимать все значения из некоторого промежутка, называется неnpерывнои случаинои величинои . Случайные величины будем обозначать заглавными буквами латинского алфавита Х, У, Z ... , а их значения - строчными буквами с индексами, например, x1, х2, хз, .. .
Законом распределения дискретной случайной величины называется соответствие между значениями x1, х2, хз, ... этой величины и их вероятностями р1,р2,рз, ....
Закон распределения дискретной случайной величины может быть задан таблично или аналитически (т.е. с помощью формул).
Если дискретная случайная величина Х принимает конечное множество значений x1, х2, ... , хn соответственно с вероятностями p1, р2, ... , рn, то ее закон распределения определяется формулами P(X=xk)=pk (k=1,2, ... n), Этот закон можно задать и таблицей,где сумма вероятностей также равна единице р1 + р2 + .. . + рn = 1. События (Х = x k ), k = 1, 2, ... , n, образуют полную группу событий, поэтому выполняется равенство для наглядности закон распределения дискретной случайной величины изображают графически, для чего в прямоугольной декартовой системе координат строят точки (Xk, Pk) И соединяют их последовательно отрезками прямых. Получающаяся при этом ломаная линия называется многоугольником распределения случайной величины Х.
Если дискретная случайная величина Х принимает бесконечную последовательность значений x1, х2, хз. .. соответственно с вероятностями р1,р2,рз... , то ее закон распределения определяется формулами
P(X=xk)=pk
(k=I,2,З, ... ),
Этот закон распределения дискретной случайной величины Х, принимающей бесконечную последовательность значений x1, х2, хз, ... можно задать и таблицей. Ряд, составленный из чисел р1,р2,рз сходится и его сумма равна единице.
12) Функция распределения случайной величины и ее свойства.
Функцией расnределения случайной величины Х называется функция действительной переменной х, определяемая равенством F(x) = Р(Х < х)где Р(Х < х) - вероятность того, что случайная величина Х примет значение, меньшее х. Геометрически это означает следующее: F(x) - вероятность того, что случайная величина Х примет значение, которое изображается точкой на числовой прямой, расположенной слева от точки х. Случайная величина называется непрерывной, если ее функция распределения F(x) = Р(Х < х) является непрерывно дифференцируемой. Вероятность того, что случайная величина Х примет значение из полуинтервала [а, b), равна разности значений ее функции распределения F(x) на концах этого полуинтервала:
Функция
распределения F(x) случайной величины
Х имеет следующие свойства.
1
Все значения функции распределения
F(x) принадлежат отрезку [О, 1], т.е.
2. Функция распределения F(x) является неубывающей, т.е. если
Х1
< х2 , то
З.
Функция F(x) в точке ХО непрерывна
слева, Т.е.
4. Если все возможные значения случайной величины Х принадлежат интервалу (а, Ь), то для ее функции распределения F(x)
5. Если все возможные значения случайной величины Х принадлежат бесконечному интервалу ( -00, + 00 ), то
Если
Х - непрерывная случайная величина,
то вероятность того, чтоона примет
одно, заданное определенное значение,
равна нулю:
поэтому
выполняются равенства:
Функция распределения F(x) для дискретной случайной величиныХ, которая может принимать значения XI, Х2, Хn С соответствующими вероятностями, имеет вид
13) Плотность распределения случайной величины и ее свойства.
Плотностью
распределения вероятности случайной
величины Х в точке х –это предел
отношения вероятности попадания
значения этой величины в интервал (х;
х+∆х) к длине ∆х отрезка [х; х+∆x]
когда ∆х→0 p(x)=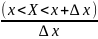
Cвойства :
1)Плотность распределения p(x) является неотрицательной функцией
P(x)≥0
2)В точках дифференцируемости функция распределения F(x), ее производная равна плотности распределения
P(x)=F`(х)
3)
Интеграл по бесконечному промежутку
(-∞ ; +∞), от плотности распределения
p(x)=1
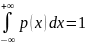
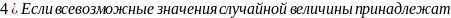
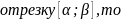
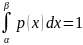
14) Математическое ожидание случайной величины.
Математическое ожидание дискретной случайно величины Х принимающей конечное множество значение с законом распределения:
P(X=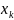
)=
,
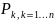
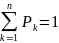называется сумма произведений ее
значений на их соответствующие
вероятности.
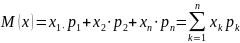
Математической ожидание дискретной случайной величины Х равно среднему арифметическому всех ее возможных значений , вследствие этого, математическое ожидание случайной величины называют средним значением.
Математическое ожидание дискретной случайной величины, принимающей бесконечную последовательность значений с законом распределения
P(X=
)=
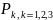, где сумма
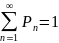определяется формулой
M(X)=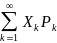
, если этот ряд сходится абсолютно.
Математическое
ожидание непрерывной случайной величины
Х , все значения которой принадлежат
отрезку (α;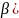
,
а p(x)
ее плотность вероятности , определяется
по формуле: M(X)=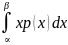
Если все значения непрерывной случайной величины Х принадлежат бесконечному промежутку (-∞;+∞), а p(x) ее плотность вероятности, то математическое ожидание определяется формулой :
M(X)=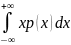
, если этот несобственный интеграл
сходится абсолютно.
Свойства Математического ожидания:
1)Значение
математического ожидания случайной
величины Х между ее наименьшим и
наибольшим значением: a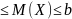
2)Математическое ожидание постоянной величины равно этой постоянной: M(C)=C
3) Постоянный множитель можно вынести за знак математического ожидания М(СХ)=СМ(Х)
4)Математическое ожидание суммы двух случайных величин , равно сумме их математических ожиданий: M(X+Y)=M(X)+M(Y)
5)Математическое ожидание разности двух случайных величин равно разности их математических ожиданий М(X-Y)=M(X)-M(Y)
6)Математическое
ожидание произведений двух независимых
случайных величин равно произведению
математических ожиданий этих величин.
M(XY)=M(X)
Распространяется на n независимых случайных величин.
15) Дисперсия случайной величины и ее свойства.
Дисперсией
случайной величины Х называется
математическое ожидание квадрата ее
отклонения : D(X)=M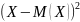
Из определения и свойств математического ожидания следует, что дисперсия любой случайной величины неотрицательна D(X)≥0
Для
вычисления дисперсии применяется
формула D(X)=M(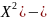
Свойства дисперсии:
Дисперсия постоянной величины равна 0.D(C)=0
Постоянный множитель можно вынести за знак дисперсии, при этом возведя его в квадрат D(CX)=
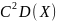
Дисперсия суммы двух независимых случайных величин D(X+Y)=D(X)+D(Y)
Дисперсия непрерывной случайной величиины Х, все значения которой принадлежат отрезку [α;β] определяется формулой :
D(X)=
Дисперсию можно вычислить по формуле D(X) =
Дисперсия непрерывной случайной величины X все значения которой принадлежат интервалу (-
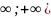вычисляется по формуле :
D(X)=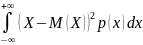
Если
этот несобственный интеграл сходится
абсолютно
Средним квадратическим отклонением случайной величины Х называют корень из ее дисперсии.
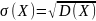
Среднее квадратическое отклонение
Разность X-M(X)называется отклонением случайной величины Х от ее математического ожидания M(X). Математическое ожидание отклонения равно 0.
M(X-M(X))=0
Средним квадратическим отклонение случайной величины Х называется корень из ее дисперсии:
Формула Бернули.
Производятся испытания в каждом из которых может появиться события А или событие не А, если вероятность события А в одном испытании не зависит от появления его в любом другом , то испытания называются независимыми относительно события А. Будем считать, что испытания происходят в одинаковых условиях, и вероятность появления события А в каждом испытании одна и та же.
Обозначим эту вероятность через p, а вероятность не А через q. P+q=1. Вероятность того, что в серии из n независимых испытаний события А появится ровно e раз и не появится
(n-k) раз обозначим через
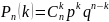-Формула
Бернули