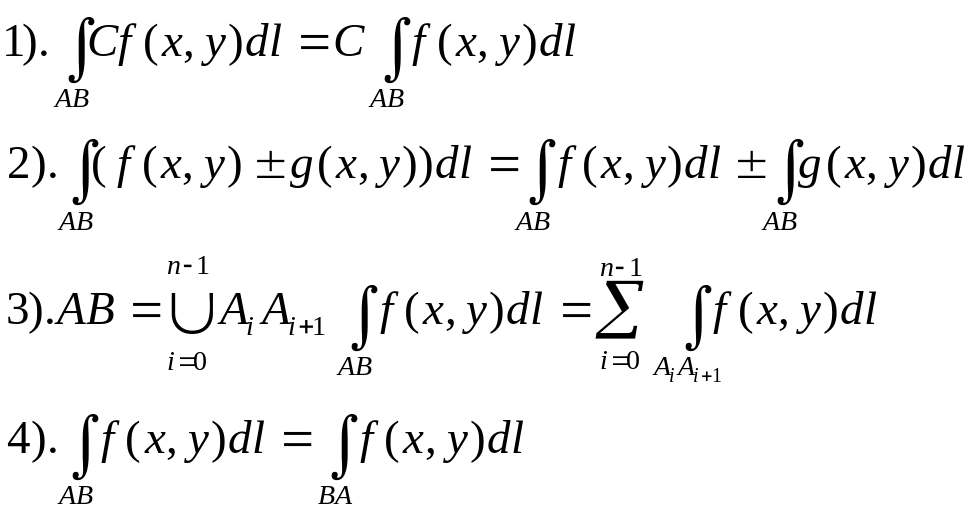8) Теорема про середнє значення для подвійного інтегралу.

Зауважимо, що якщо f(x,y) не від’ємне в області D, ця теорема, має слідуючи геометричну інтерпретацію. Об’єм циліндричного бруса обмеженого зверху поверхнею z=f(x,y) дорівнює об’єму циліндра, основою якого є область D, а вистою

Обчислення подвійного інтеграла

Припустимо f(x,y)є C(D) f(x,y)>=0 для довільного (x,y)єD. За геометричною інтерпритацією подвійного інтегралу:

Об′єм тіла обмеженого знизу обл D, з боків циліндричними поверхнями, твірні яких пар-ні oz а напрямною їх є границя обл D.

Припустимо, що

Перерізом даного тіла є криволінійна трапеція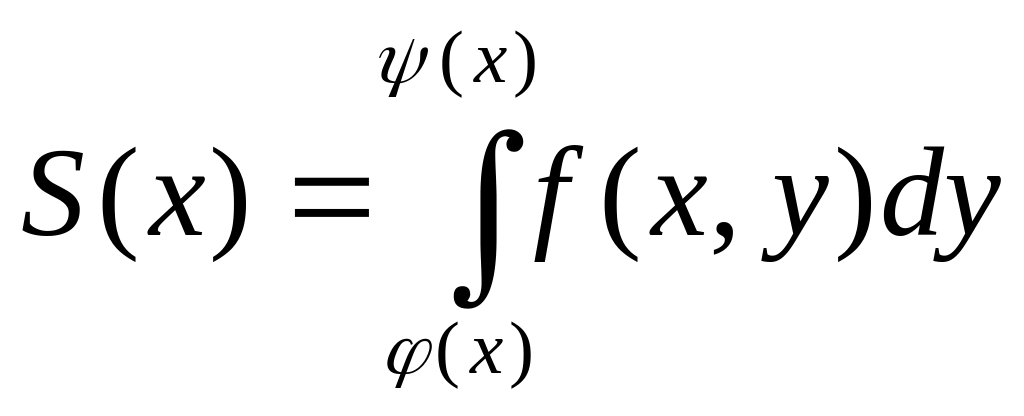

Відомо, що об′єм тіла довільної форми можна обчислити за доп визн інтегралу

Пі дставимо значення до першого виразу і маємо:

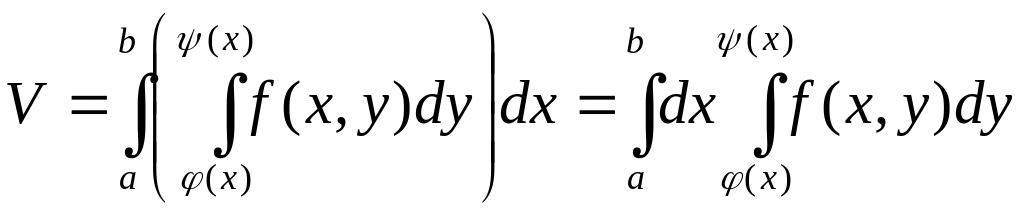
Одержаний інтеграл наз повторним інтегралом

Прирівнюючи вираз маємо:

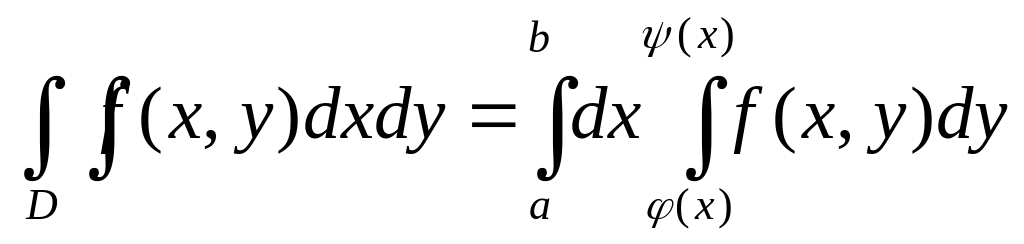
Зауважимо, що одержана формула має місце для дов області і довільної інтегровної ф-ї.

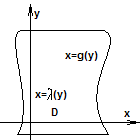
Зауважимо, якщо

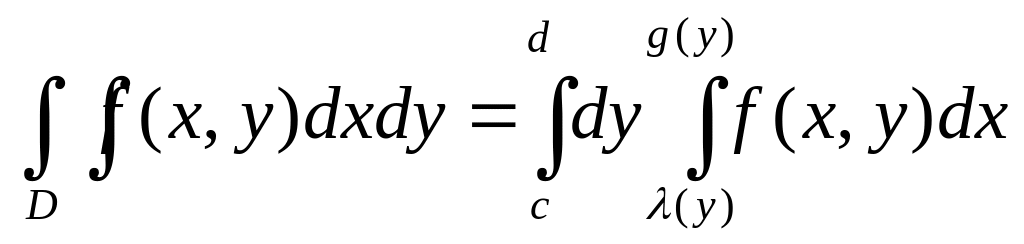
Якщо область не є елементарною ні відносно 0х ні 0у, тоді за допомогою прямих пар-х коорд осям, цю область розб на частини, кожна з яких є елементарною відносно ох або оу. Обчислюють інтеграл по кожній із областей і результати додають.

Заміна змінних у подвійному інтегралі.

П рипустимо задано обл D обмежена К.

Установлює взаємо-однозначну відповідність між областями D і Δ. М(х,у) ставить єдину точку N(U,V) у обл Δ. Припустимо, що ф-ї (1) неперервні і мають неперервні частинні похідні по кожній із змінних в Δ.

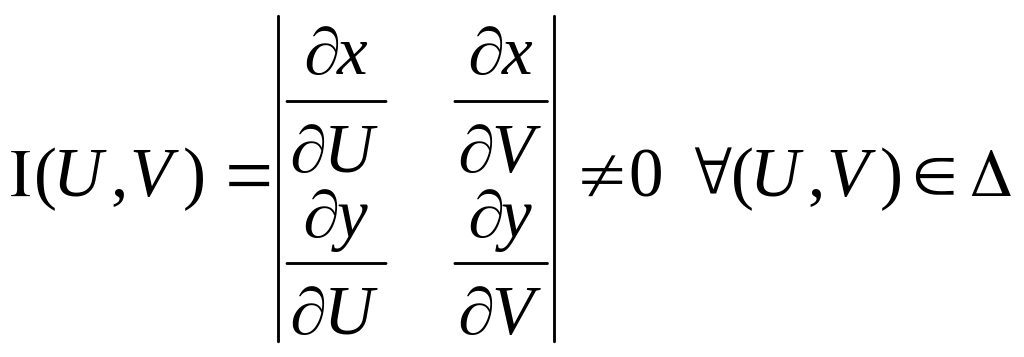
Визначник Якобі (Якобіан)

Т. Якщо f(x,y) є C(D), а система ф-й (1) задов всі вищеперелічені умови, тоді має місце слідуюча формула:

У частковому випадку коли в ролі зміннихU V виступають полярні координати (1) має вигляд:

Формула приймає вигляд:

Обчислення площі плоскої фігури

Якщо в обл D f(x,y)=1 для дов (x,y) є D тоді

Обчислення об’ємів тіл

Із геометричної інтерпретації подвійного інтегралу маємо, що об’єм тіла, обмеженого знизу обл. D пл. ХОУ, з боків – циліндричними поверхнями, твірні яких паралельні вісі OZ, а зверху – поверхнею z=f(x,y) обчисл. за формулою

Зауважемо, що якщо тіло у просторі обмежено знизу поверхнею z=f₁(x,y), зверху- z=f₂(x,y) і проекцією на ХОУ є обл. Д.

Обчислення площі кривої поверхні

Якщо поверхня S задана явним р-ням z=f(x,y) і проекцією поверхні S на пл. ХОУ є обл. D, тоді якщо f(x,y) має неперервні частинні похідні по кожній із змінних в обл. D, тоді:

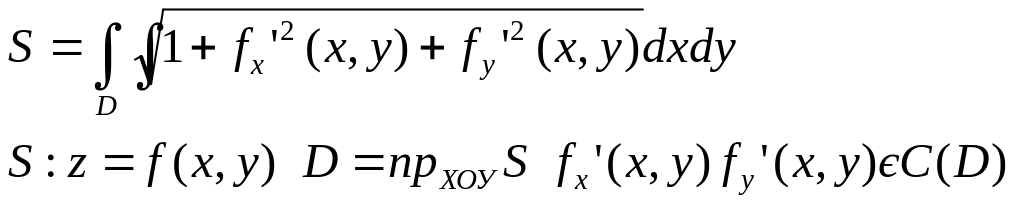
Фізичні застосування подвійного інтегралу

Припустимо, що на пл. ХОУ задана обл.Д, пл. якої і в обл.D зосереджена маса Δm, тоді

є середньою густиною розподілу маси обл.Д

Нехай M(x,y)єD

густина розподілу маси обл.D

Надалі будемо припускати, що густина розподілу маси в кожній т. обл.Д і є неперервною в обл.D ρ(x,y)єС(D)

Обчислення маси плоскої області

Нехай на пл.ХОУ задана обл.D В кожній точці обл.D густина розподілу маси відома: ρ(x,y)єС(D). Щоб знайти масу обл.Д

Довільним способом розбиваємо обл.Д

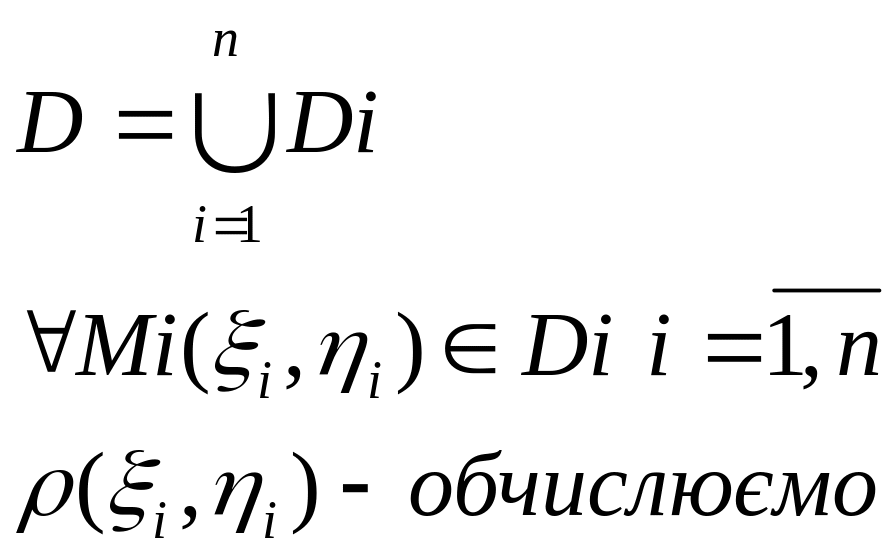
Далі припускаючи, що ρ в кожній точці обл.D одна і таж і дор. значенню ρ в т.Мі одержимо, що маса обл.Dі:

Обчислення статичних моментів плоскої обл.

Статичним моментом матеріальної т.М, в якій зосереджена маса m, відносно прямої l наз. добуток маси, зосередженої в т.М на відстань точки до даної прямої: m*d. У випадку системи мат. точок М1,...,Мn, в яких зосережені маси m1,...,mn, під статичним моментом розуміють суму:

Припустимо, що на пл.ХОУ задана обл.Д, в кожній т. якої відома ρ(x,y)єС(D)

Знайти статичні моменти обл.Д відносно координатних осей. З цією метою:

Припускаючи, що маса обл.Dі зосереджена в точці Аі одержемо, що статичний момент обл.Ді

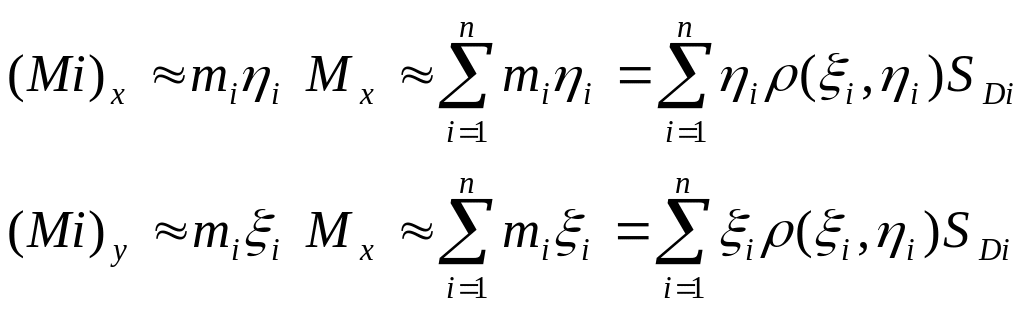
Точні означення статичних моментів плоскої обл.D одержимо, якщо в останніх двох співвідношеннях перейдемо до границі, коли махS_Di→0:

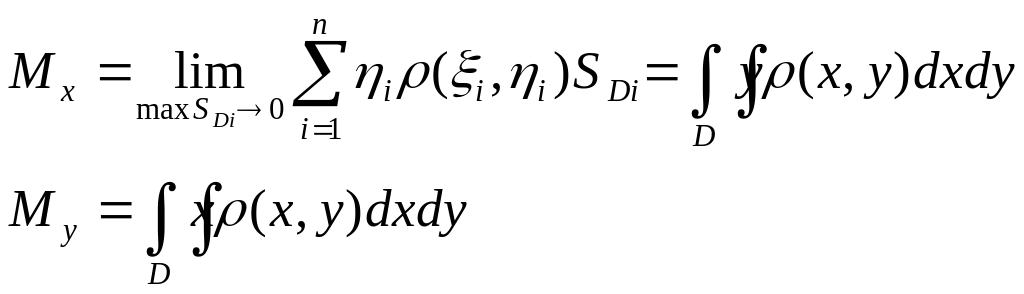
Обчислення координат центру мас плоскої області.

Центром мас плоскої області D наз. т.М з координатами (Хс,Ус), яка має слідуйчу властивість:

Якщо в т.М зосередити масу всієї обл.D, то статичні моменти цієї точки відносно координатних осей дор. Статичним моментам всієї обл.D відносно тих же осей.

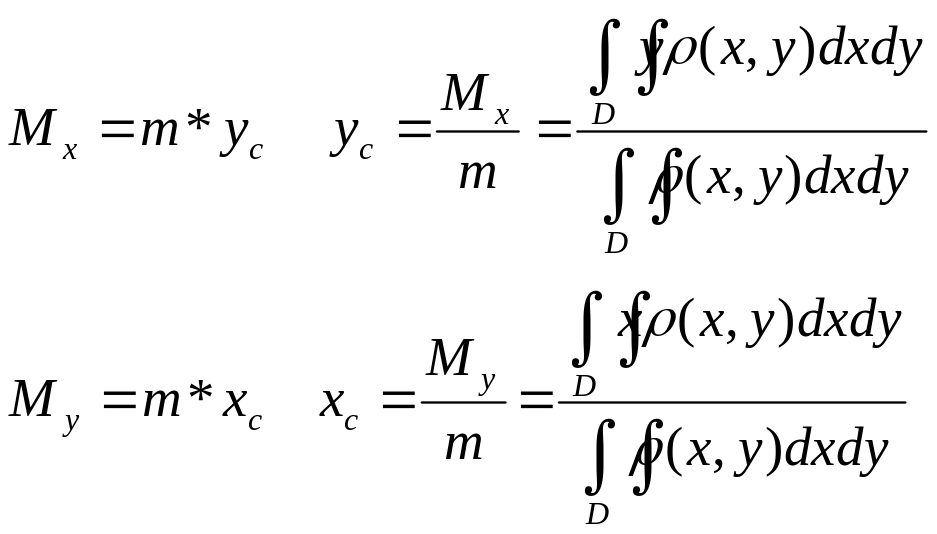
Обчислення моментів інерції плоскої області відносно координатних осей.

Моментом інерції мат. точки, масою m відносно деякої прямої наз. добутк m на квадрат відстані до данної т.

У випадку системи мат. точок, в яких зосереджені маси m₁,…,m_n під моментом інерції цих точок розуміють:

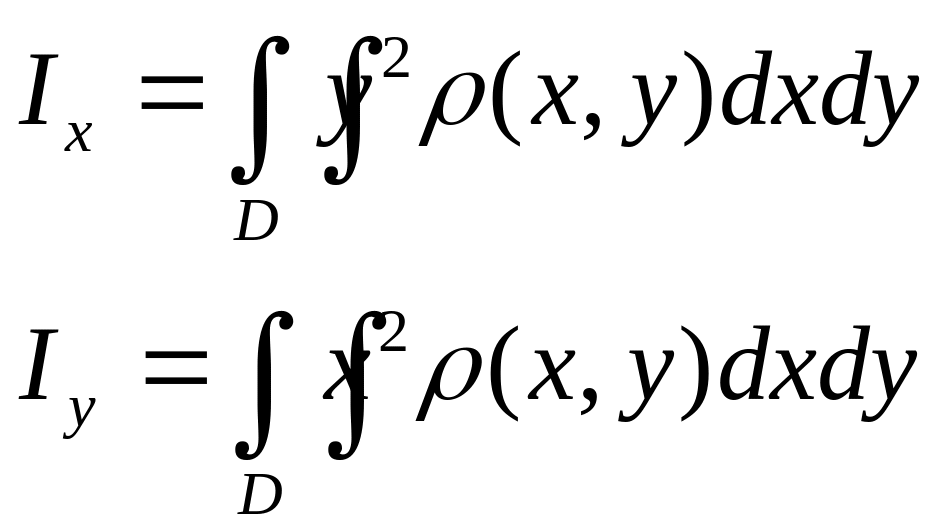
Під полярним моментом (моментом інерції відносно початку координатних осей) розуміють суму моментів інерції відносно координатних осей.

Потрійний інтеграл

Припустимо, що у 3-хмірному просторі задана область V, обмежена поверхнею S. В кожній точці f(x;y;z) зробимо слідуюче:

1) Довільним способом неперервними поверхнями область V розіб’ємо на V частин

- інтегральна сума Рімана для потрійного інтегралу від f(x;y;z) по області V. Значення цієї суми залежить від способу розбиття області V на часткові області Vi та від вибору точок Mi в кожній із часткових областей.

4)

при умові що вона не залежить від способу розбиття області V на часткові області Vi та від вибору точок Mi в кожній із часткових областей наз. ПОТРІЙНИМ ІНТЕГРАЛОМ від f(x;y;z).

По області Vi позн. так:

Обчислення потрійного інтегралу

Якщо Z1(x,y), Z2(x,y) неперервні в D, а f(x,y,z) є C(V), тоді:

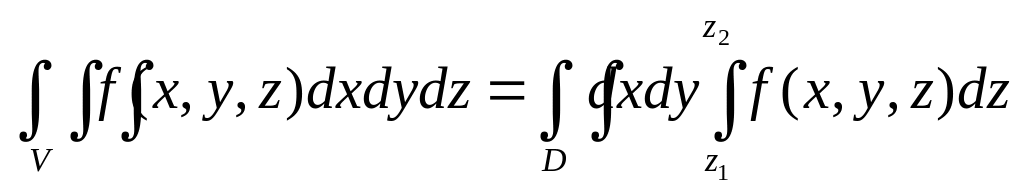
Якщо

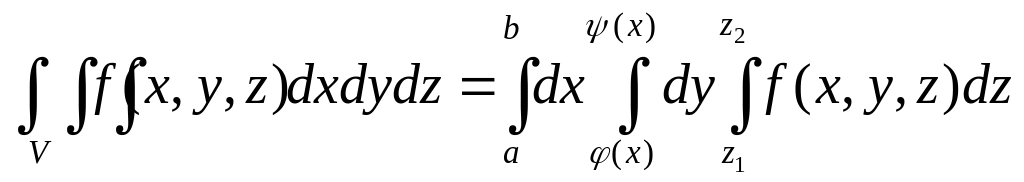
Заміна змінних у потрійному інтегралі

x=x(U,V,W), y=y(U,V,W), z=z(U,V,W)

(U,V,W)= (1)

(1) в кожному внутрішній точці області V ставлять у відповідність внутрішню точку області , а кожн. граничній точці області V (1) ставлять у відповідність граничну область . Припустимо, що функції системи (1) – неперервні і мають неперервні частинні похідні по кожн. із змінних в об-ті , при чому

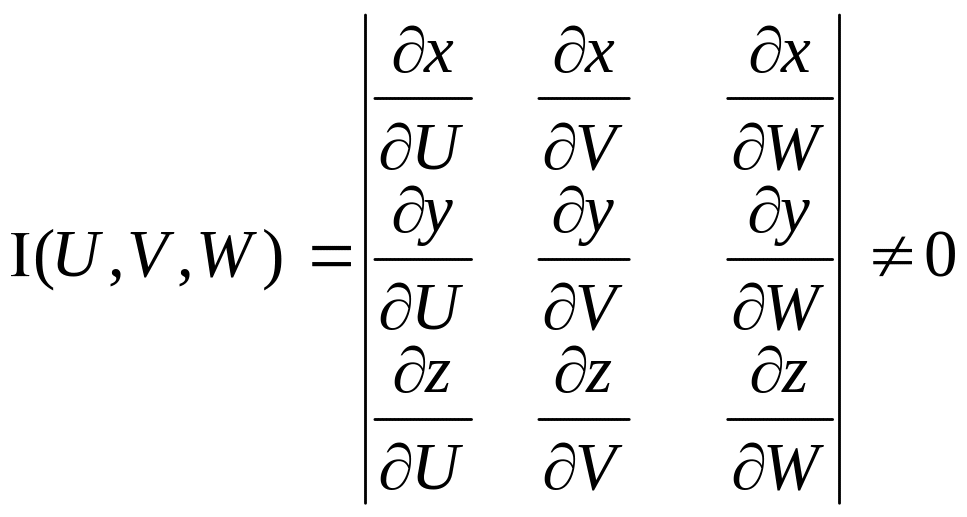
Теорема. Якщо f(x,y,z)єC(V), а система функцій (1) задовольняє всі вищезазнач. умови, тоді

модуль Якобіана

Циліндричні координати

Цил-ні коорд-ти – об’єднання координат на площині із звичайною декартовою апплікатою z. Формули переходу від декартових до циліндричних координат:

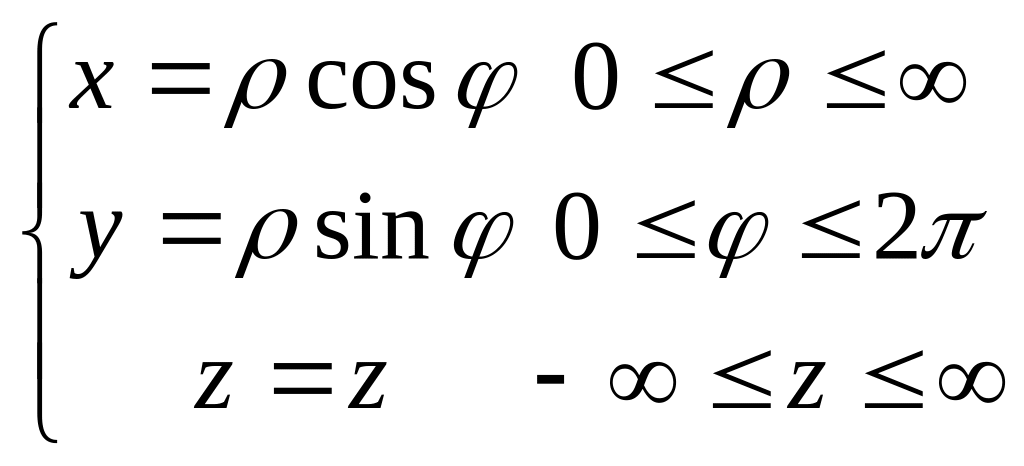
Знайд. Якобіан переходу від декарт. Координат до циліндричних:

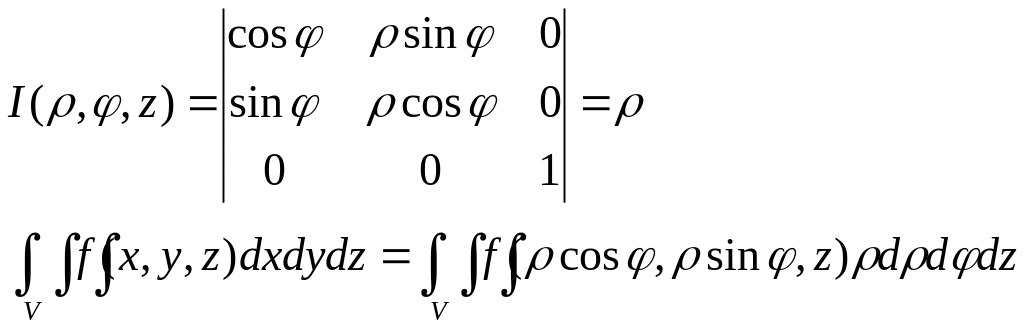
Сферичні координати

Сферичними координатами наз. Полярні координати у просторі

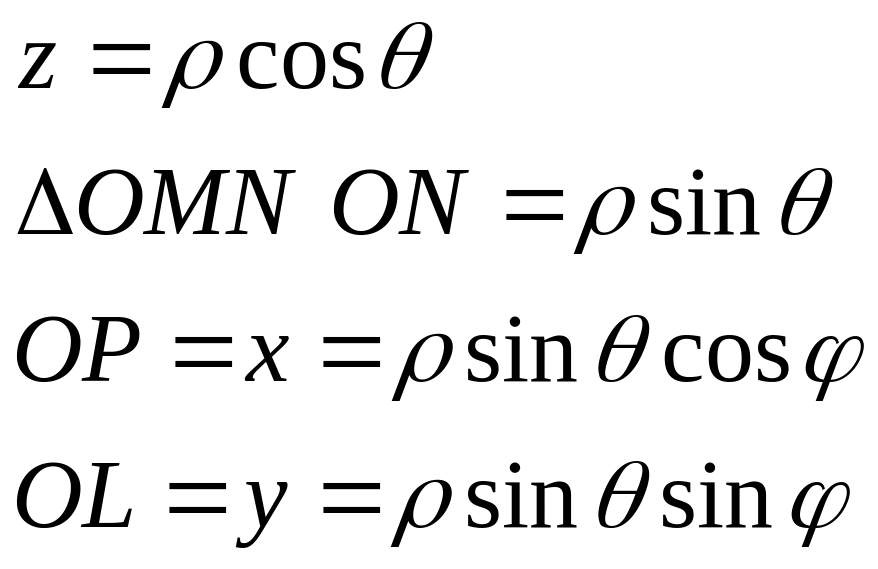
Ф-ла заміни змінних при переході від декартових до сферичних

Обчислення об’ємів тіл довільної форми

Фор-ли статичних моментів та координат центру мас

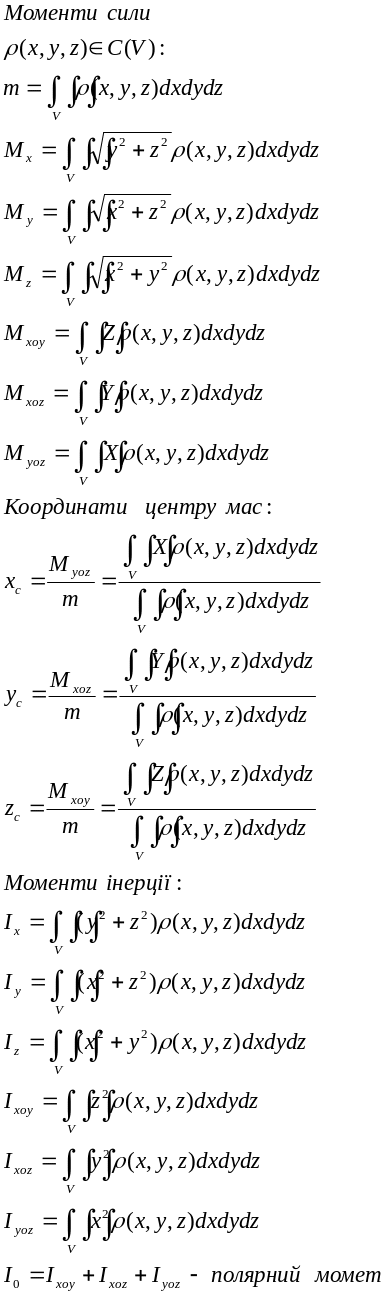
Криволінійні інтеграли першого роду

Прип, що на пл XOY задана напрямна крива AB, в кожній точці кривої задана ф-ція двох змінних f(x,y).

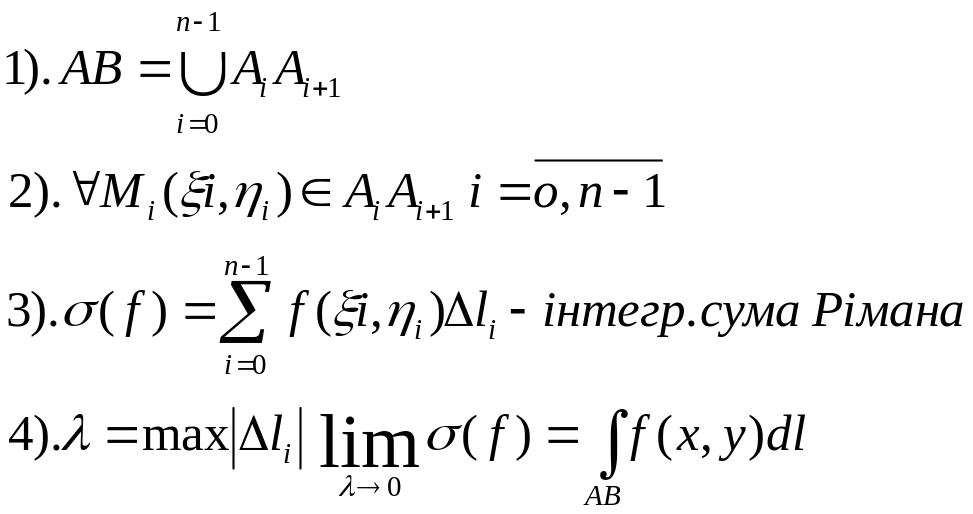
Властивості криволінійного інтегралу першого роду