Обчислення криволінійного інтегралу і роду

1) явне

АВ:у=у(х) хє[а,b] у(х)є[а,b]

2) якщо крива АВ задана параметричним рівнянням

3) якщо крива задана:

АВ:=() є[,]; ()єС[,] тоді якщо f(x,y)єС(AB):

4) Крива задана у просторі задана параметр-ичним рівнянням

де

f(x,y,z)єC(A,B) то:

Геометричні та фізичні застосування криволінійного інтегралу І роду:

Обчислення довжини дуги кривої

f(x,y)=1 для довілних (х,у)є(А,В) тоді

Переходячи в останній рівності до границі l0

Обчислення маси:

Якщо в кожній точці кривої АВ задана густина розподілу маси, яка (х,у)єС(АВ) тоді:

Статичні моменти плоскої кривої відносно координатних осей:

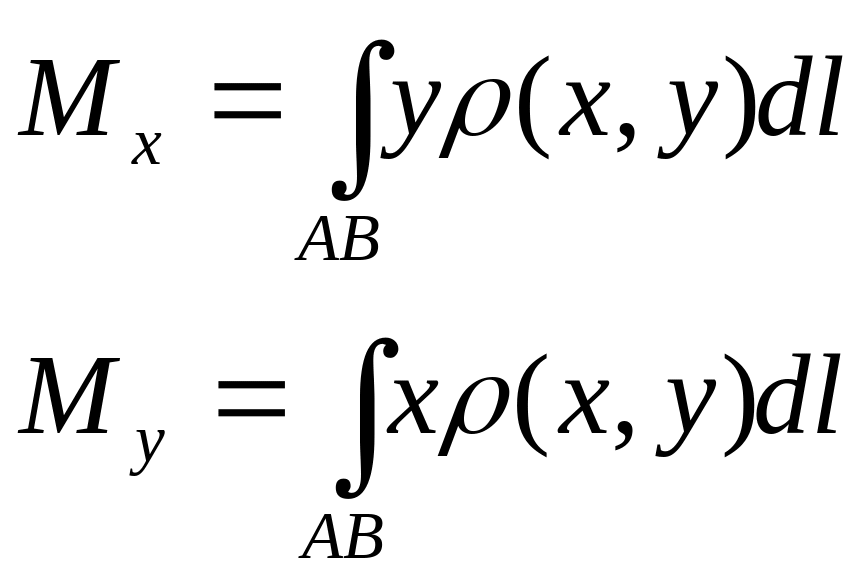
Обчислення статичний момент кривої у просторі відносно координатних осей:

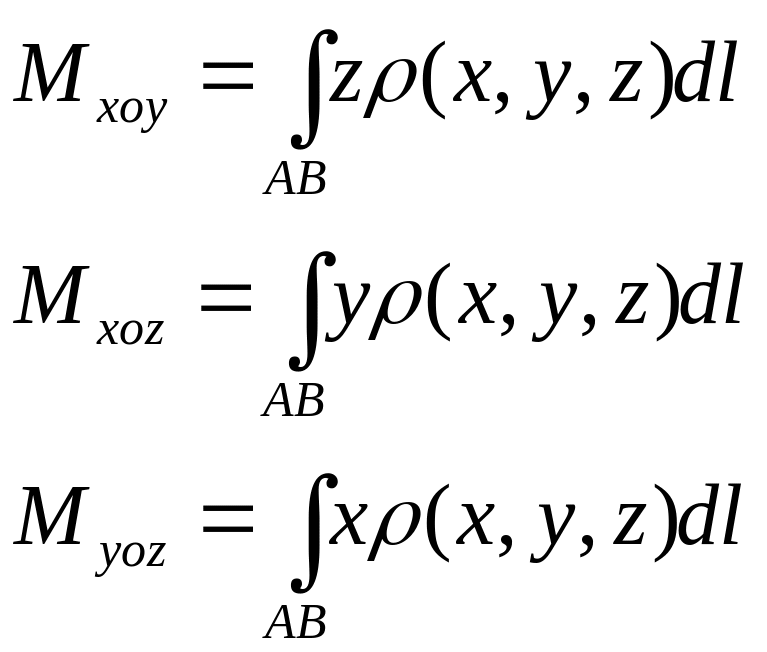
Координати центру мас плоскої кривої:

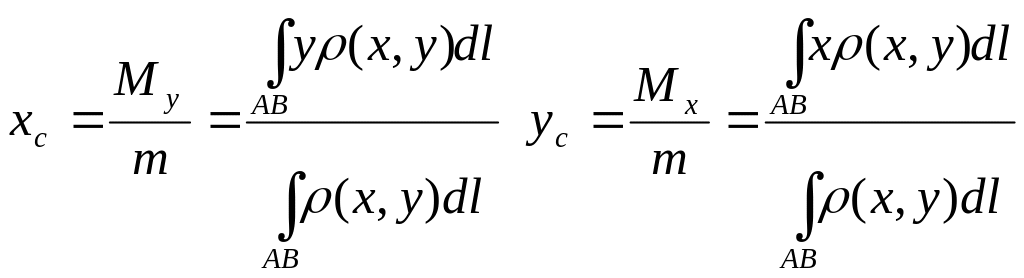
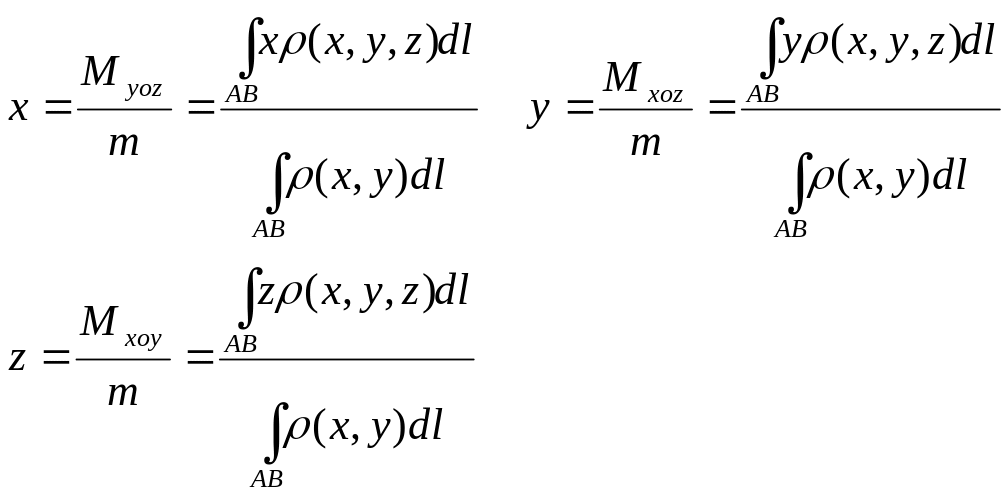
Криволінійний інтеграл ІІ роду

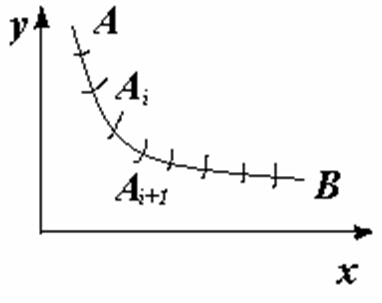
Формально:

Нехай A_i(x_i,y_i) A_i+1(x_i+1,y_i+1);

x_i=x_i-x_i+1 y_i=y_i-y_i+1

2) дов. M_i(_i,_i)єА_іА_і+1

побудуємо суми :

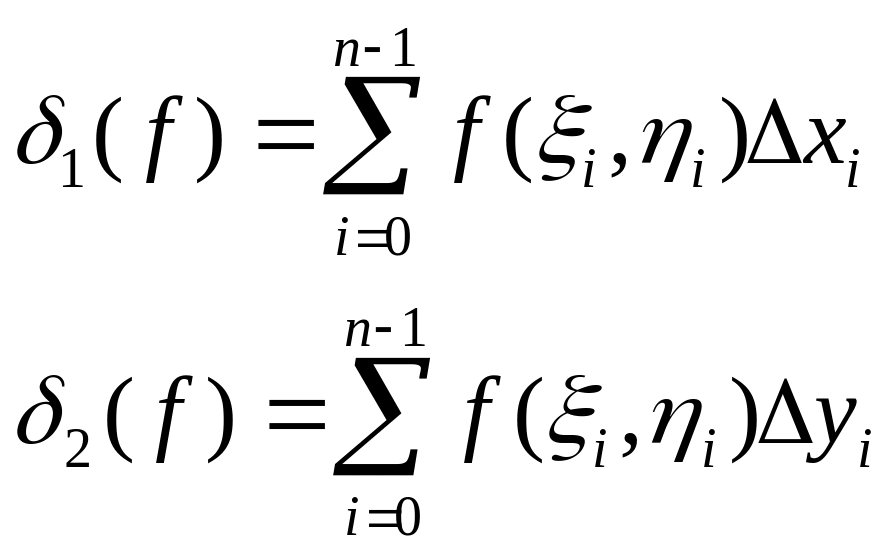
Ці суми наз. інтегральними сумами Рімана для криволінійного інтегралу ІІ роду по кривій АВ від функції f(x,y), значення цих сум залежить від способу розбиття кривої АВ на часткові криві й A_iA_i+1 та від вибору точок М_і на кожній із часткових прямих.

4) =maxl_i

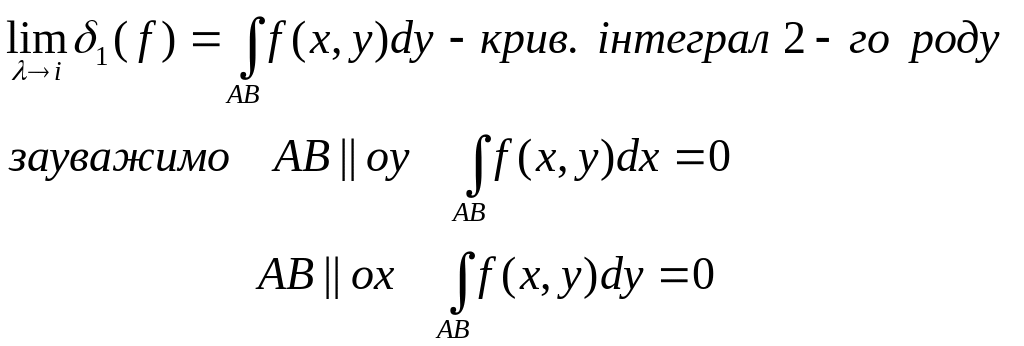
Припустимо, що Р(х,у) та Q(x,y)-задані дві функції при чому:

Сума цих двох криволінійних інтегралів

наз. криволінійним інтегралом ІІ роду загального типу

У ПРОСТОРІ

Аналогічно АВ:f(x,y,z) то

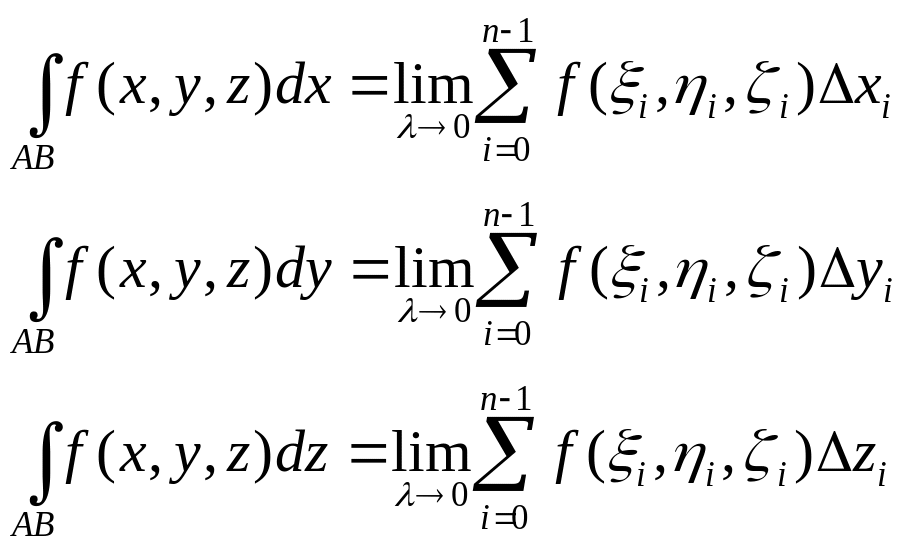
Припустимо, що Р(х,у,z) та Q(x,y,z) R(x,y,z)-задані 3 функції при чому:

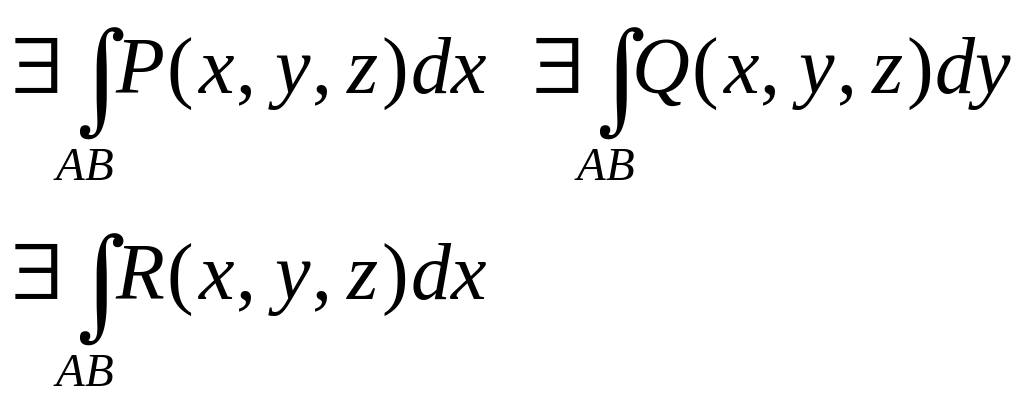
Сума цих двох криволінійних інтегралів наз.

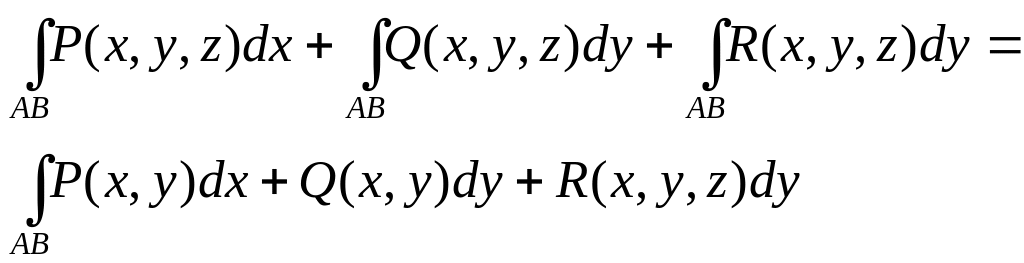
криволінійним інтегралом ІІ роду загального типу

Обчислення криволінійного інтегралу 2 роду

Теорема 1

Якщо ф. P(x,y)=Q(x,y)C(A,B) В точках кривої AB, а крива AB задана загальним рівнянням y=y(x), x[a,b] і ф. y(x) [a,b], тоді

Teрема 2

Якщо ф. P(x,y)=Q(x,y)C(A,B), а крива AB задана параметричними рівняннями

, де t[,] і ф. y(t), x(t) мають неперервну похідну на відрізку [,] тоді

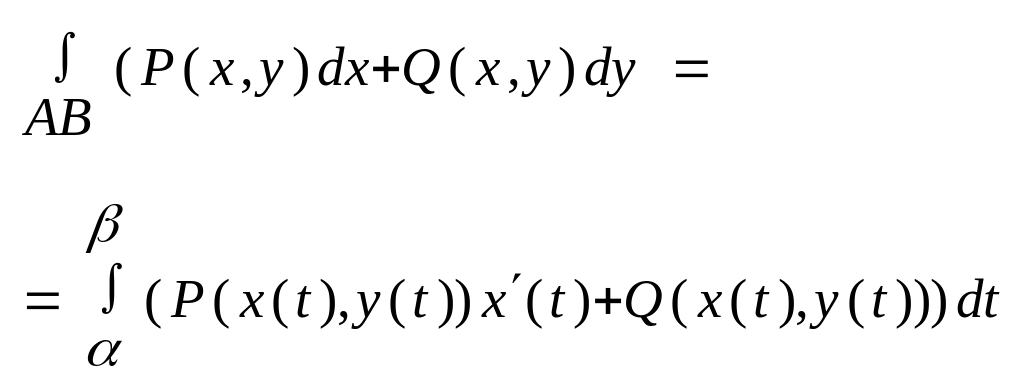
Теорема 3

Якщо ф. P(x,y) і Q(x,y)C(A,B), а крива AB задана рывн. У полярних коорд.

AB: =() :[,]

`()C[,]

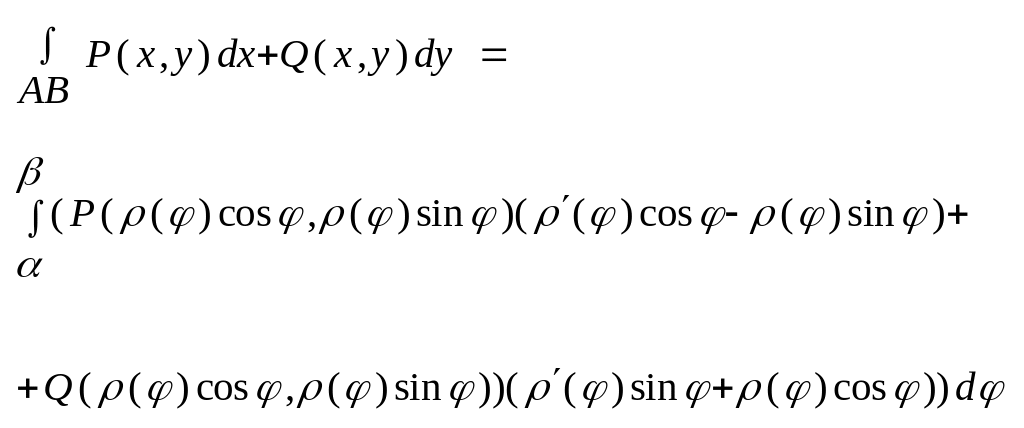Теорема 4

Якщо P(x, y, z),Q(x, y, z) і R(x, y, z) C(A,B), а крива AB задана параметричним рівнянням

AB: і , тоді

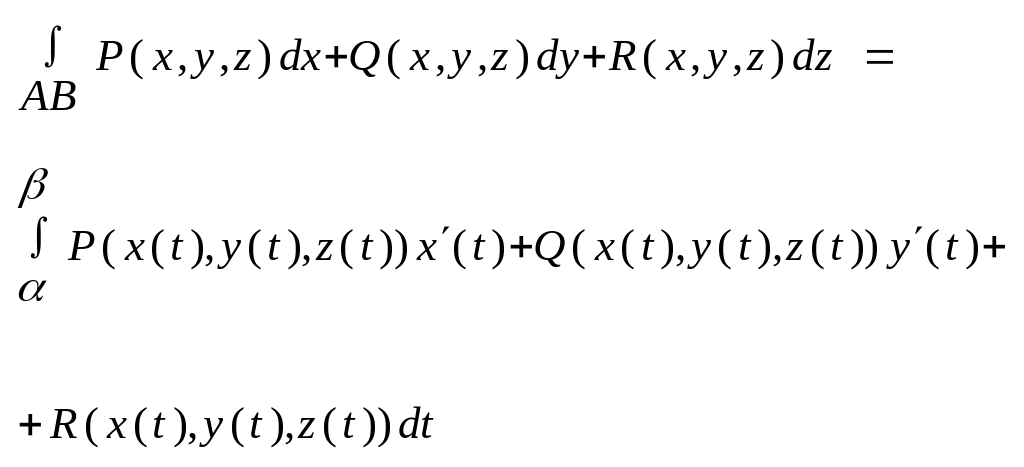
Обчислення криволінійного інтегралу зводиться до обчислення визначеного інтегралу

Звязок між криволінійним інтегралами 1 та 2 родів

Припустимо, що на площ. XoY, задана крива AB, в точках кривої AB, задані 2 неперервні ф. P(x,y), Q(x,y)(A,B)

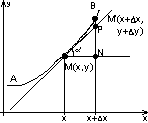
Нехай т.M(x,y) – деяка фіксована т. кривої AB.

Надамо т. x приросту △x

MN=△x

M’N=△y △MP’N

PN=tg=’(x)△x=dy

Позначимо MP=dl із △MPN=>dl²=dx2+dy²

dx=dl*cos

dy=dl*sin

Формула звя’зку між інтегралом 1 і 2 родів:

Якщо AB – крива у просторі, в т.якої задані 3 функції :

P(x, y, z), Q(x, y, z), R(x, y, z)C(A,B),то

, де cos

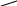cos напрямні косинуси

cos дотичної проведеної до графіка кривої в т.з абсцисою x, y, z.

Формула Гріна

Формула Гріна установлює зв’язок між криволінійним інтегралом 2 роду по замкненій кривій на площині та подвійним інтегралом по області , яку ця крива обмежує.

Припустимо, що на площині XoY задана елементарна відносно вісі Ox, області D.

Обмежена з двох боків x=a, x=b.

Зверху y=(x), знизу y=(x)

Припустимо, що в області D

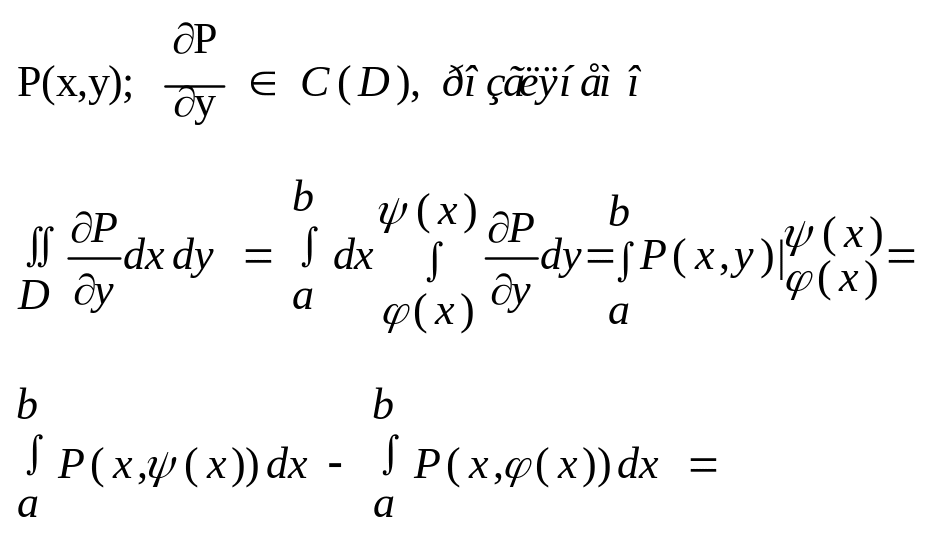
викор. формулу для обчисл. криволінійного інтегралу 1 роду, маємо.

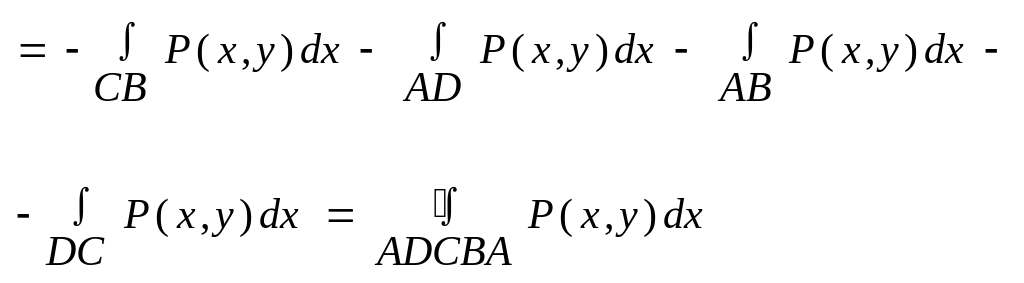
Зауважимо, що якщо область D не є елементарною відносно вісі Ox, та за допомогою прчмих, паралельних коордн. осям, що цю область розбивають на частини, кожна з яких э елементарною відносно вісі Ox, потім приміняють одержану формулу до кожної із одержаних областей і всі результати додаємо, враховуючи при цьому, що криволінійний інтеграл по допоміжним лініям, зустрічається двічі в протилежних нпарямках, а тому сумма всіх цих криволінійних інтегралів дор. 0, і тому одержимо, що формула:

має місце для довільної області D

Розмырковуючи аналогічно (як вище) можна показати, що якщо в області D задана ф. Q(x,y) , яка є неперервною в області D разом зі своєю частинною похідною по області

Віднімаючи від останньої формули попередню

–ф-ла Гріна

Теорема про незалежність криволінійного інтегралу від шляху інтегрування.

В області D задані

P(x,y), Q(x,y),

Слідуючі умови еквівалентні:

2). Криволінійний інтеграл не залежить від шляху інтегрування:

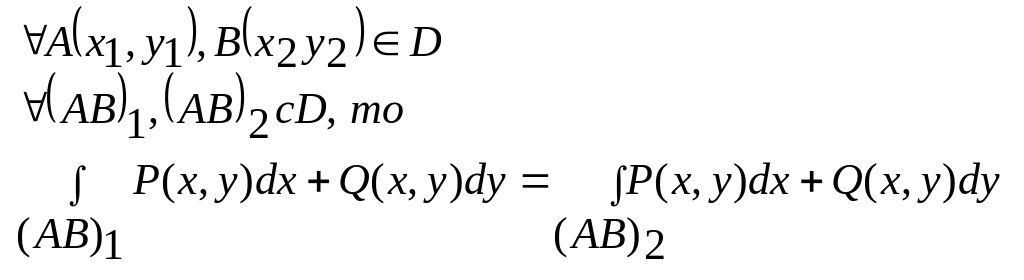
3). 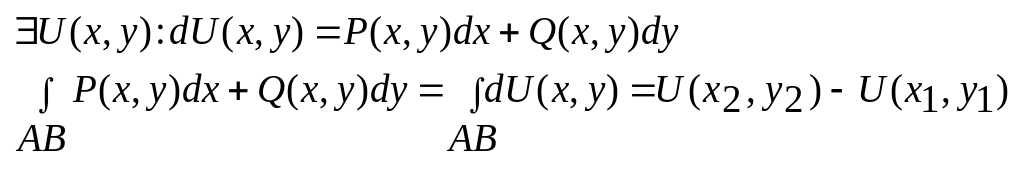4).

Поверхневі інтеграли першого роду

Формально зробимо:

1) розіб’ємо S на n частин

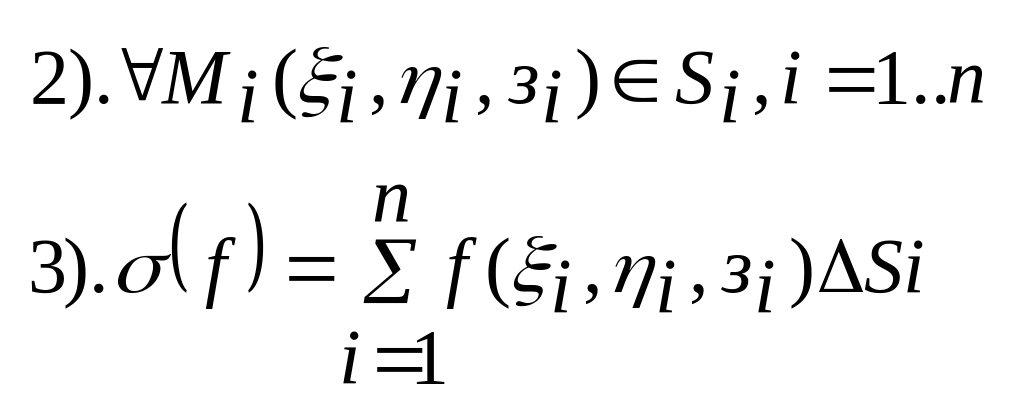
- інтегральна сума Рімана, залежить від способу розбиття поверхні S на часткові поверхні та вибору точок М_і на кожній із часткових поверхонь

Поверхневий інтеграл першого роду- скінчена границя при умові, що вона не залежить від способу розбиття поверхні S на часткові поверхні та вибору точок М_і на кожній із часткових поверхонь

Обчислення поверхневого інтегралу першого роду

Т1.

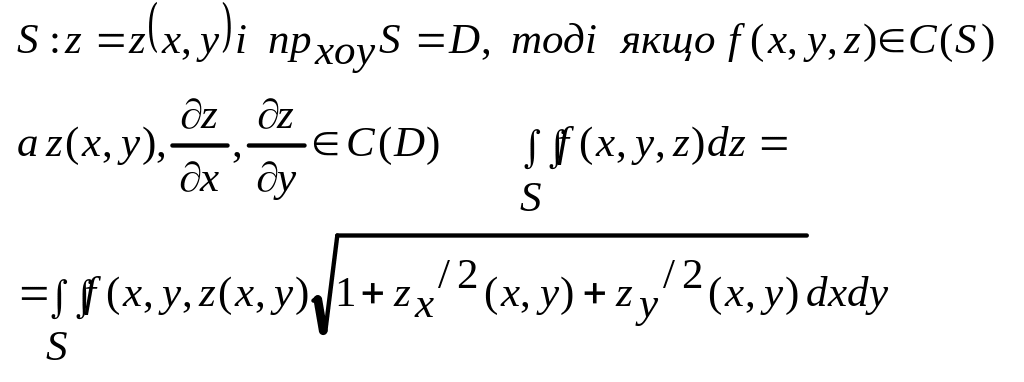
T2.

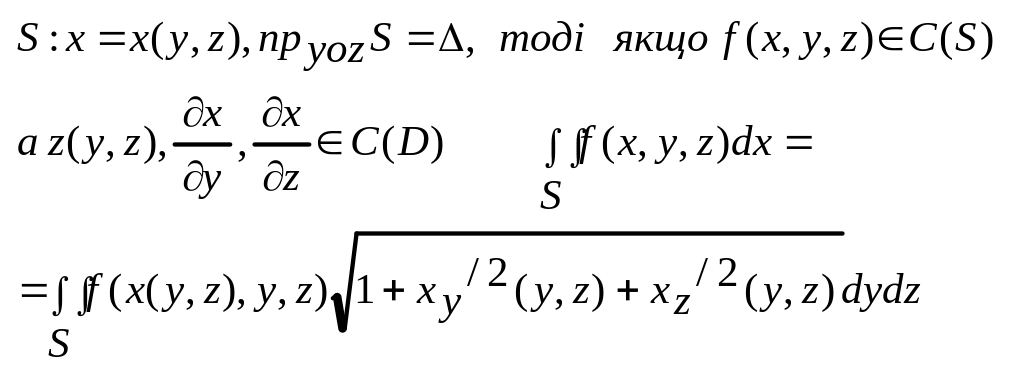T3.

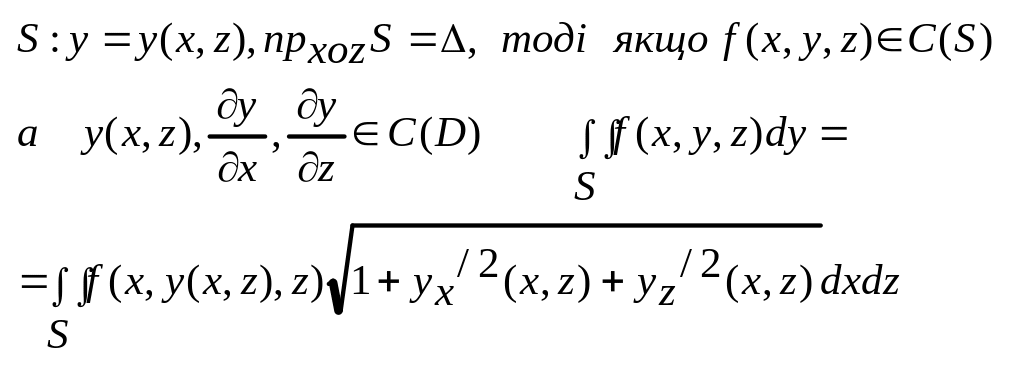T4.

Функції x,y,z мають неперервні частинні похідні по кожній із змінних по області Δ, тоді якщо має місце:

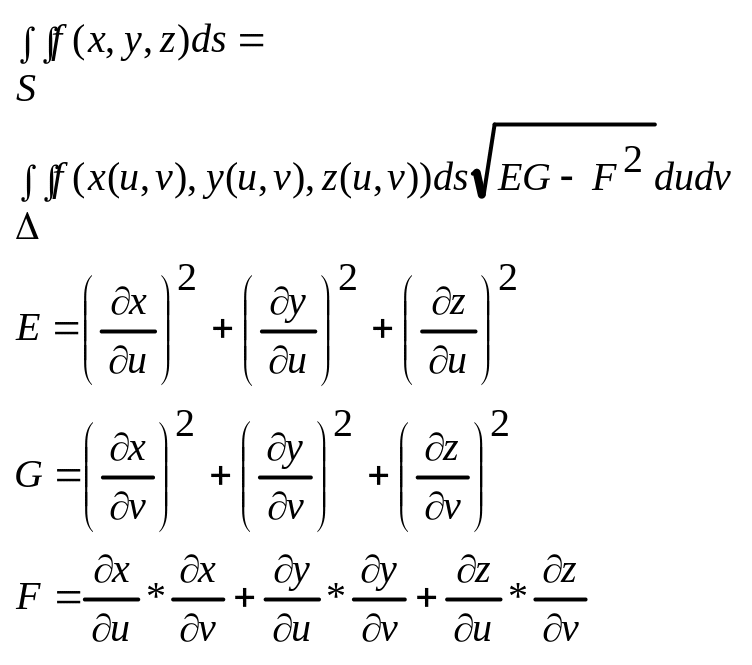
Поверхневі інтеграли 2 роду

Поверхня називається односторонньою, якщо довільна точка поверхні, рухаючись по довільному замкненому контуру на поверхні повертається в початкове положення з тим же напрямком нормалі.

В противному випадку поверхня двостороння.

Додатна (верхня) сторона – сукупність точок поверхні, косинус кута між нормаллю та додатнім напрямком вісі oz більше 0.

В противному випадку – внутрішня.

Нехай задана поверхня S. Формально зробимо:

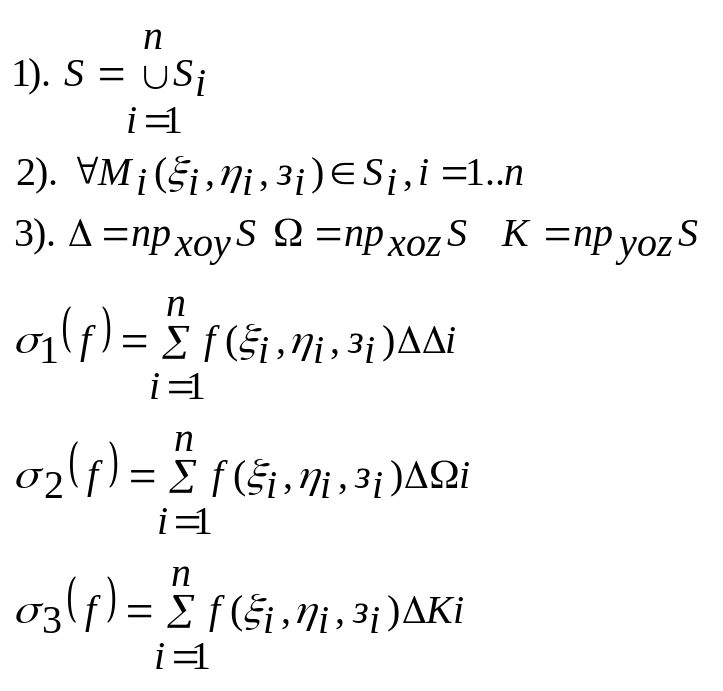
- інтегральні суми Рімана, залежать від способу розбиття поверхні S на часткові поверхні та вибору точок М_і на кожній із часткових поверхонь

Поверхневий інтеграл II роду- скінчена границя при умові, що вона не залежить від способу розбиття поверхні S на часткові поверхні та вибору точок М_і на кожній із часткових поверхонь

при умові, що ця границя не залежить від способу розбиття поверхні S на часткові поверхні Sі та від вибору т. Мі на кожній із часткових поверхонь називається поверхневим інтегралом 2-го роду від f(x, y, z) по поверхні S.

Аналогічно:

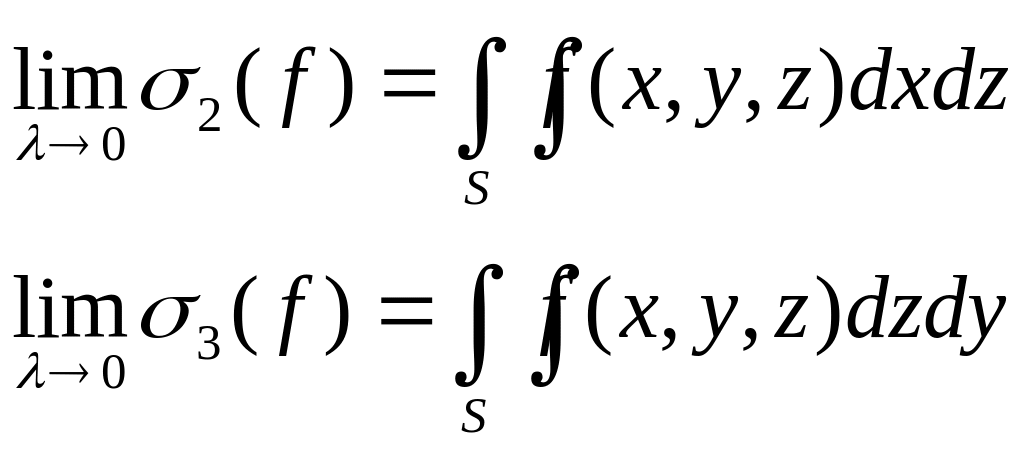
Якщо:

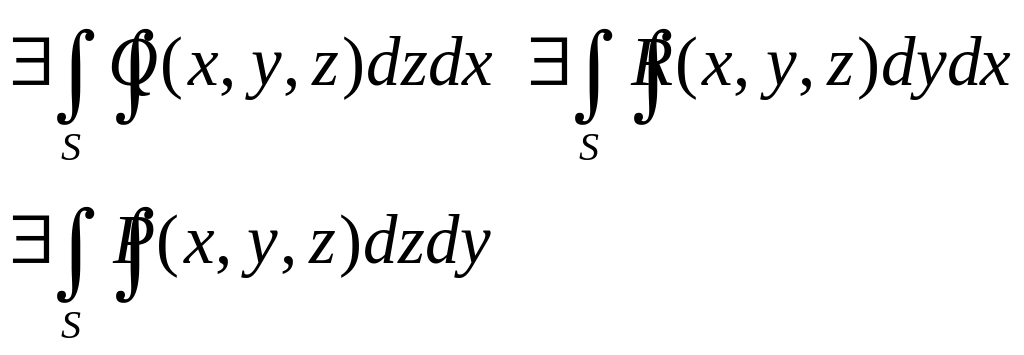
Сума цих трьох поверхневих інтегралів називається поверхневим інтегралом 2-го роду загального типу.

Обчислення поверхневого інтегралу 2 роду

Теорема1:

Якщо пов. S задана явними р-нями Z=Z(x,y) i D=ПР.хоуS, тоді, якщо f(x,y,z) є С(S), Z=Z(x,y) є С(D), то має місце формула:

Теорема2:

Якщо S задана: Х=Х(y, z), Δ=ПР.уozS, f(x,y,z) є C(S),

Х(y, z) є С(Δ), то

Теорема3:

Якщо S задана: У=У(х, z), Ω =ПР.xozS, f(x,y,z) є C(S),

У(х, z) є С(Ω), то

Зв’язок між поверхневими інтегр 1-го та 2-го родів

Якщо ф-ції P(x,y,z), Q(x,y,z), R(x,y,z) є С(S), то поверхневий інтеграл суми цих ф-цій дорівнює

∫_S∫(P(x,y,z)cos(n^x)+Q(x,y,z)cos(n^y)+ R(x,y,z)cos(n^z))dS.

ЗАУВАЖЕННЯ! Якщо S – замкнена поверхня, то на знаку поверхневого інтегр. ставлять О:

Формула Остроградського

Ф-ла Остроградського установлює зв’язок між пов. інт. По замкненій поверхні S та потрійним інт. по області, яку ця поверхня обмежує.

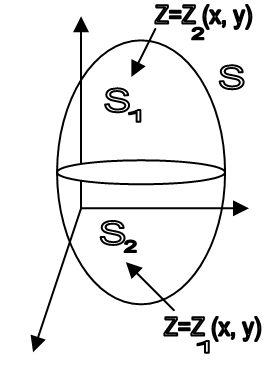
Припустимо, що в ОХУZ задана поверхня S, якаа обмежує область V. Припустимо, що в області V заданна ф-ціія R(x,y,z), δR/δz є С(V). Розглянемо:

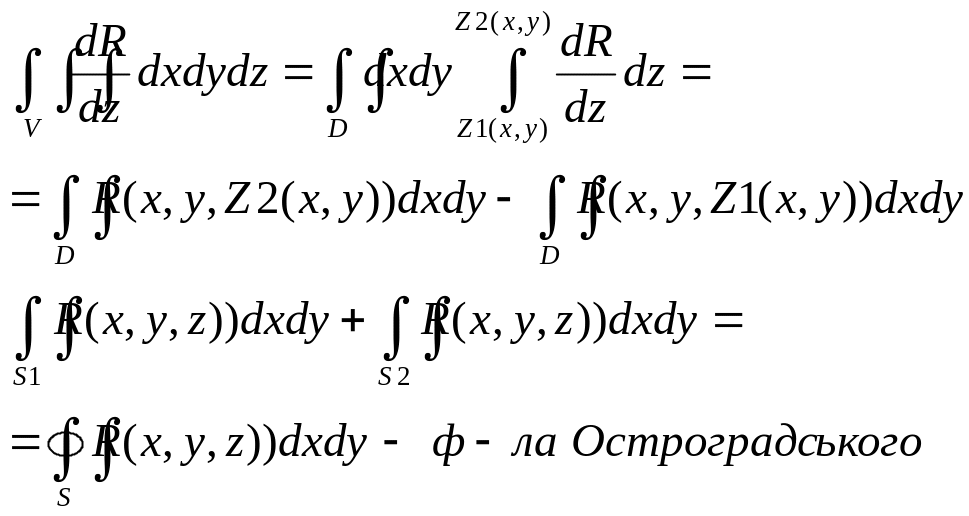
Формула Стокса

Формула Стокса установлює зв’язок між криволінійним інтегралом 2-го роду по кривій у просторі та поверхневим інтегралом по поверхні, яка натягнута на цю криву.

Якщо в т. поверхні та в т. кривої, на яку ця поверхня натягнута, задані три неперервні ф-цій P(x,y,z), Q(x,y,z), R(x,y,z), які мають неперервні частинні похідні по кожній із змінних, то має місце ф-ла:

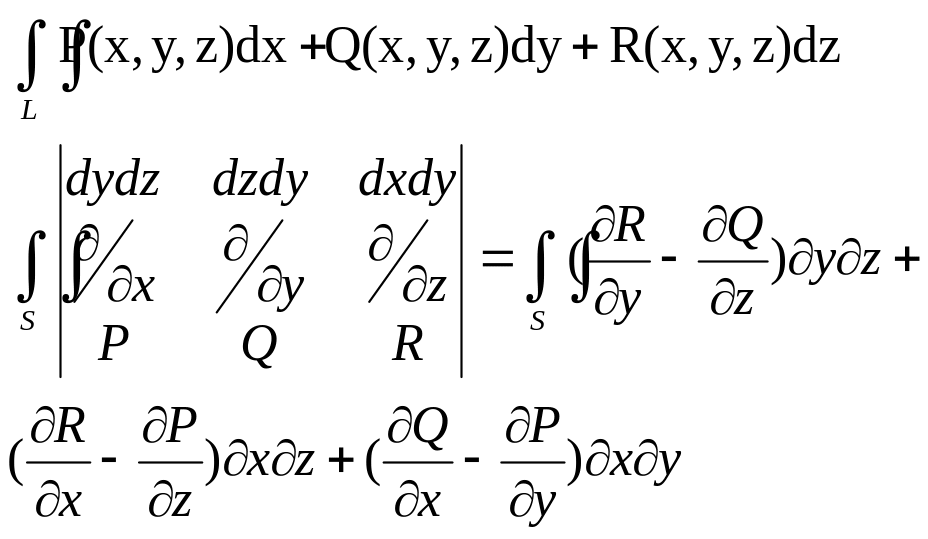ЗАУВАЖИМО! Що якщо Р і Q залежать тільки від (х,у), а R(x,y,z) = 0, то ф-ла Стокса має вигляд:

1).Функціі багатьох змінних

Числові послідовності в n-мірному просторі

Поняття функціі багатьох змінних

Границя функцій багатьох змінних

Неперервність функціі в точці

Частинні похідні ф-ціі багатьох змінних

2).Диференційовність ф-ціі багатьох змінних в точці

Необхідні умови диференційовності ф-ціі в точці

Достатня умова диференційовності ф-ціі в точці

Геометр інтерпритац повного диференц ф-ції в точці

3).Диференційовність ф-ції багатьох змінних

Похідна ф-ціі по заданному напрямку

4).Частинні похідні вищих порядків

Диференціали вищих порядків

Формула Тейлора для ф-цій багатьох змінних

5).Екстремум ф-ціі багатьох змінних

Необхідна умова існув екстрем ф-ціі багатьох змінних

Достатня умова існування екстремуму

Достатня умов існування екстрем. ф-ціі двох змінних

Задача про обчислення об’єму циліндричного бруса

6).Поняття подвійного інтегралу

Умови існування подвійного інтегралу

Властивості подвійного інтегралу

Теор. про середнє значення для подвійного інтегралу.

7).Обчислення подвійного інтеграла

Обчислення подвійного інтеграла

Заміна змінних у подвійному інтегралі

Обчислення площі плоскої фігури

Обчислення об’ємів тіл

Обчислення площі кривої поверхні

8).Фізичні застосування подвійного інтегралу:

Обчислення маси плоскої області

Обчислення статичних моментів плоскої обл.

Обчислення координат центру мас плоскої області.

Обчислення моментів інерції плоскої області відносно координатних осей.

9).Потрійний інтеграл

Обчислення потрійного інтегралу

Заміна змінних у потрійному інтегралі

Циліндричні координати

Сферичні координати

10).Ф-ла заміни змінн при перех від декарт до сферичн

Обчислення об’ємів тіл довільної форми

Фор-ли статичних моментів та координат центру мас

Криволінійні інтеграли першого роду

Властивості криволінійного інтегралу першого роду