5. Властивості оцінок, що одержані за методом найменших квадратів

Якщо виконати всі передумови, то оцінки, що одержані за МНК, є BLUE:

B (best) – найкращі,

L (lineart) – лінійні,

U (unbiased) – незміщені,

E (ectimator) – оцінка.

Найкраща – має найменшу дисперсію серед усіх незміщених оцінок (одержаних за іншими методами). Наприклад, за методом максимальної правдоподібності. Цей метод використовується якщо з точністю до невідомих значень параметрів відомий загальний вид закону ймовірності вибіркових даних. Для оцінки параметрів його використовують при регресійному аналізі в рамках нормальної класичної моделі, коли додається ще одне припущення: про нормальний розподіл регресійних залишків.

Якщо порушені вимоги постійності дисперсії залишків та їх незалежності, то оцінки, що розраховані за МНК, стають не найкращі (не ефективні), але залишаються незміщеними та консистентними (спроможними, умотованими). Оцінка є спроможною, якщо її дисперсія при збільшенні числа спостережень прямує до нуля:

Ця властивість є асимптотична при умові незміщеності.

Лінійна – оцінка лінійно функціонально залежить від вибіркових спостережень.

Незміщена – математичне сподівання оцінки параметра дорівнює значенню параметра в генеральній сукупності.

Ця властивість має місце при відсутності систематичної похибки в визначенні положення лінії регресії, що слідкує із умови M(U)=0.

6. Оцінка параметрів нелінійних функцій

При оцінці параметрів нелінійних моделей частіш проводять їх до лінійного вигляду шляхом логарифмування або заміни змінних, а потім використовують МНК.

Розглянемо порядок побудови нелінійної моделі на прикладі степеневої функції (рис. B) . За допомогою перетворювача (наприклад, логарифмічного підсилювача) одержимо , тобто лінійну залежність відносно логарифмів змінних. Її стає краще видно, якщо провести заміну: Y=lg y; X=lg x; A=lg a. Тоді маємо Y=A+bX і за МНК, згідно формул 6а, 10 знаходимо:

; Y=A+bX .

Ми знайшли оцінки параметрів відносно логарифмів змінних, а для знаходження оцінок необхідно зробить обернене перетворювання (потенціювання): , тоді .

При таких перетвореннях треба бути уважними, так як критерії значущості та інтервальні оцінки параметрів для нормальної лінійної регресії потребують нормального закону розподілу логарифма вектора збурення, а не самого вектора.

При побудові моделі, що задана в вигляді (рис. С) перетворення за допомогою логарифмування неможливе, тому проводять заміну змінних , тоді

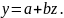
В подальшому рахуємо:

Модельні значення для відповідних значень х_і , що подаються із вхідного масиву даних через ответвитель. За допомогою пристрою порівняння рахуємо складові вектора збурення , використовуючи значення у_і також із вхідного масиву даних. На основі аналізу вектора збурення оцінюється якість побудованої моделі і, за відповідними критеріями, приймається рішення про здатність моделі до прогнозування.

Матеріал, що необхідно повторити для вивчення лекції:

1. Знаходження екстремуму функції декількох змінних.

2. Частинні похідні.

3. Логарифмування та потенціювання функцій.

4. Нормальний закон розподілу випадкової величини.