4 Анализ устойчивости исследуемой аср

4.1 Критерий Гурвица

Критерий устойчивости, предложенный в 1895г. Швейцарским математиком Гурвицем, получил широкое распространение благодаря своей относительной простоте. Критерий Гурвица формулируется следующим образом: чтобы корни характеристического уравнения системы автоматического регулирования

при a₀ > 0 имели отрицательные вещественные части (т.е. система устойчива), необходимо и достаточно, чтобы главный определитель и все его диагональные миноры были положительны.

Для определения устойчивости АСР по критерию Гурвица необходимо использовать знаменатель выражения (1.4), то есть характеристическое уравнение системы в замкнутом состоянии:

(4.1)

4.096*10^-6*p⁴+7.68*10^-4*p³+0.048*p²+p+10.097=0

Для уравнения третьего порядка (n = 4) получаем условия Гурвица:

А0 > 0, А1 > 0, А2 > 0, А3 > 0, А4  0

Все коэффициенты уравнения (4.1) положительны, следовательно, одно условие Гурвица выполнено. Вторым условием для системы третьего порядка является положительность определителя ∆2 . Вычислим его.

Определитель ∆2 положительный, следовательно, выполнено и второе условие Гурвица, т.е. система устойчива.

Определим граничный коэффициент усиления системы:

=0,

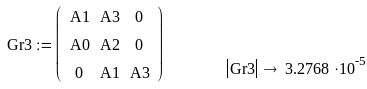
Тогда граничный коэффициент усиления разомкнутой системы К_гр:

4.2 Исследование устойчивости с помощью критерия Михайлова

Согласно криерию Михайлова, замкнутая САУ устойчива, если годограф, начинаясь при  =0 на положительной действительной оси огибат с ростом  от 0 до  против часовой стрелки начало координат, обходя последовательно в положении направления n квадрантов и не обратиться в 0.

Построение характеристик осуществим с помощью прикладной программы Mathсad при изменении  от 0 до 90.

Рисунок 4.1 - Годограф Михайлова

Как видно из рисунка годограф огибает четыре квадранта и не обращается в ноль, значит согласно криерию Михайлова замкнутая САУ устойчива.

Построим годограф Михайлова в ограниченном диапазоне частот (для определения граничного коэффициента усиления). Характеристика приведена на рисуеке 4.2.

Рисунок 4.2 - Годограф Михайлова в ограниченном диапазоне частот

По данному рисунку видно, что Кгр = 55 рад/с.

5 Построение частотных характеристик

Если на вход заданной системы подать синусоидальное воздействие Xвх = Ax () *sin (t), то на ее выходе в установившемся режиме будет

Xвых = Ax () *sin (t + ()), (5.1)

Выражение (5.1) – это амплитудно–фазовая частотная характеристика заданной АСР. Если заменить оператор Лапласа на оператор Фурье в выражении (2.6), то можно получить уравнение амплитудно – фазовой характеристики системы:

Выделив в последнем выражении вещественную и мнимую части получим:

W(jω) = P(ω) + jQ(ω) ( 5.2)

Построение частотных характеристик осуществим с помощью прикладной программой Mathсad при изменении ω от 0 до ∞ (рисунки 5.1 – 5.3).

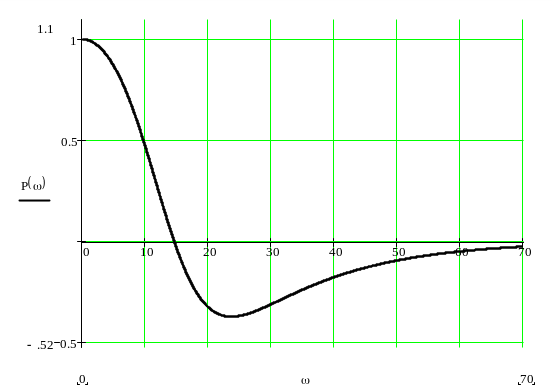
Рисунок 5.1 – Вещественная частотная характеристика заданной АСР

Рисунок 5.2 – Мнимая частотная характеристика заданной АСР

Рисунок 5.3 – Амплитудно–фазовая частотная характеристика заданной АСР

Уравнение амплитудной и фазовой частотных характеристик:

Изменяя частоту ω от 0 до ∞ в выражениях (3.3) и (3.4) при помощи прикладной программы MathCAD строим характеристики системы, представленные на рисунках 5.4 и 5.5.

Рисунок 5.4 – Амплитудно-частотная характеристика заданной АСР

Рисунок 5.5 – Фазо-частотная характеристика

Графики логарифмической амплитудной частотной характеристики и логарифмической фазовой частотной характеристики данной системы представлены на рисунках 5.6 и 6.7.

Рисунок 5.6 - График логарифмической амплитудной частотной характеристики

Рисунок 5.7 - График логарифмической фазовой частотной характеристики