Задания для самостоятельной работы

1. Брошены две игральные кости. Построить пространство элементарных событий. Найти вероятность того, что сумма выпавших очков равна 4?

2. Монета подброшена два раза. Какова вероятность того, что оба раза выпадет герб?

3. В лотерее 1 000 билетов. Из них 500 выигрышные и 500 – невыигрышные. Куплено 2 билета. Какова вероятность того, что оба билета выигрышные?

4. В группе 30 учеников. На контрольной работе 6 учеников получили оценку «отлично», 10 – «хорошо», 9 – «удовлетворительно». Какова вероятность того, что все 3 ученика, вызванные к доске, имеют неудовлетворительные оценки по контрольной работе?

5. Точка взята наудачу внутри круга радиуса R. Найти вероятность того, что эта точка окажется от центра на расстоянии, меньшем r (r < R).

6. По цели произвели 24 выстрела, причем было зарегистрировано 19 попаданий. Найти частоту поражения цели.

7. В конверте среди 100 фотографий находится одна разыскиваемая. Из конверта наудачу извлечены 10 фотографий. Найти вероятность того, что среди них окажется нужная.

8. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди извлеченных деталей:

а) нет бракованных; б) нет годных.

9. В ящике 9 белых шаров и 1 черный. Вынули сразу 3 шара. Какова вероятность того, что все шары белые?

Тема 24. Основные теоремы о вероятности

24.1. Теоремы о вероятности событий

Теорема сложения вероятностей несовместных событий. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

.

Обобщение теоремы на случай произвольного конечного числа попарно несовместных событий: .

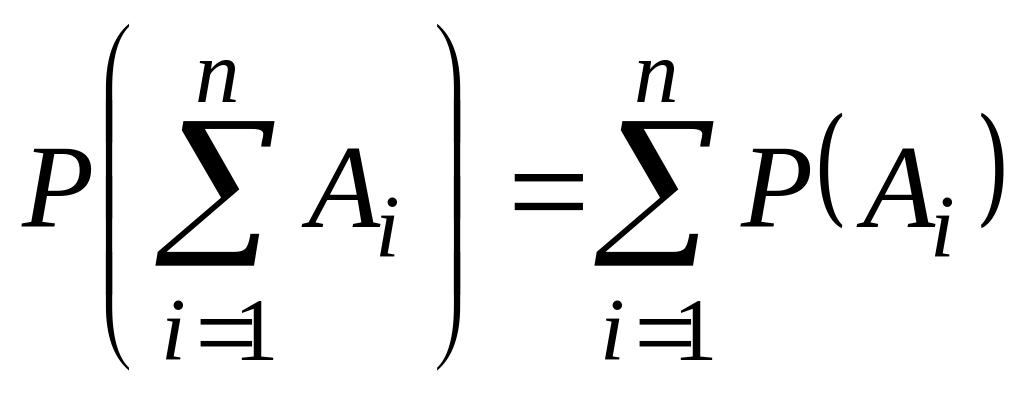Пример 1. В ящике 30 шаров: 10 красных, 5 синих и 15 белых. Вынули один шар. Найти вероятность появления цветного шара.

Решение. Появление цветного шара означает появление либо красного, либо синего шара. Пусть событие – появление красного шара, а событие – появление синего шара. Тогда событие + – появление цветного шара. Вероятность события : . Вероятность события : . Появление шара одного цвета исключает появление шара другого цвета, поэтому события А и несовместны. По теореме о сложении вероятностей несовместных событий .

Определение 1. Событие называют независимым от события , если вероятность события не зависит от того, произошло событие или нет.

Определение 2. Событие называют зависимым от события , если вероятность события меняется в зависимости от того, произошло событие или нет.

Определение 3. Вероятность события , вычисленную при условии, что имело место другое событие , называют условной вероятностью события А и обозначают .

Теорема умножения вероятностей. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:

, если события и зависимы;

, если события и независимы.

Обобщение теоремы на случай произвольного конечного числа независимых событий: .

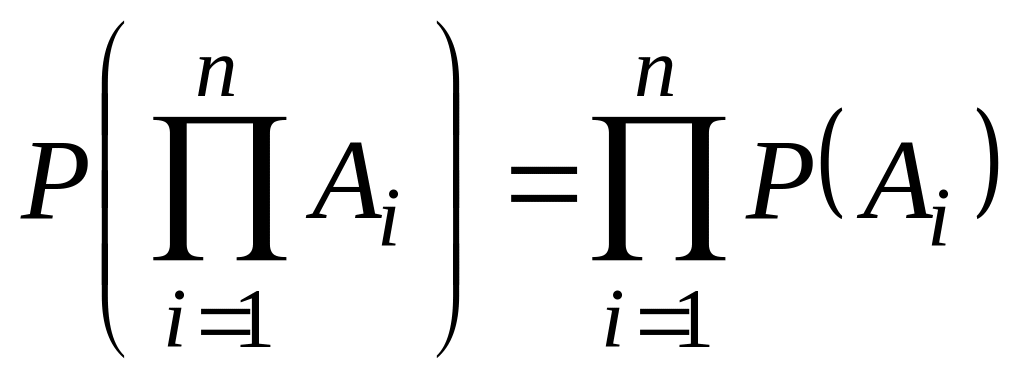Следствие. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.

Пример 2. В ящике находится 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в ящик. Найти вероятность того, что при первом испытании появится белый шар, при втором – черный и при третьем – синий.

Решение. Пусть событие – при первом испытании появится белый шар, событие – при втором испытании появится черный шар; событие – при третьем испытании появится синий шар. Вероятность появления белого шара при первом испытании . Вероятность появления черного шара при втором испытании, вычисленная в предположении, что при первом испытании появился белый шар, то есть условная вероятность . Вероятность появления синего шара в третьем испытании, вычисленная в предположении, что при первом испытании появился белый шар, а при втором черный, равна . Так как события , и совместны, то искомая вероятность

.

Пример 3. Вероятность того, что стрелок при одном выстреле попадет в мишень, равна . Стрелок произвел три выстрела. Найти вероятность того, что он попал три раза.

Решение. Пусть событие – стрелок попал в мишень при первом выстреле, событие – стрелок попал в мишень при втором выстреле; событие – стрелок попал в мишень при третьем выстреле. Вероятности этих событий по условию равны между собой: . Так как вероятность попадания в цель при каждом из выстрелов не зависит от результата остальных выстрелов, то все три события независимы, то .

Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

.

Пример 4. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: , . Оба орудия выстрелили по цели. Найти вероятность попадания хотя бы одним из орудий.

Решение. Пусть событие – попадание в цель первого орудия, событие В – попадание в цель второго орудия. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А и В независимы. Вероятность события АВ (оба орудия попали в цель) равна . Так как события А и В совместны, то искомая вероятность .

Теорема о вероятности появления хотя бы одного из совокупности независимых событий. Вероятность появления хотя бы одного из независимых событий А₁, А₂, …, А_n равна разности между единицей и произведением вероятностей противоположных событий , , …, : .

Пример 5. Вероятности попадания в цель при стрельбе из трех орудий соответственно равны: , , . Найти вероятность попадания хотя бы одним из орудий при одном залпе из всех орудий.

Решение. Пусть событие – попадание в цель хотя бы одним из орудий при одном залпе из всех орудий, событие А₁ – попадание в цель первым орудием, А₂ – попадание в цель вторым орудием, А₃ – попадание в цель третьим орудием. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому события А₁, А₂, А₃ независимы. Вероятности событий, противоположных событиям А₁, А₂, А₃ (то есть вероятности промахов), соответственно равны:

;

;

.

Тогда искомая вероятность .

Теорема о полной вероятности. Пусть событие может произойти вместе с одним из событий , , …, (гипотез), образующих полную группу попарно несовместных событий. Тогда вероятность события можно определить по формуле

.

Пример 6. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а вероятность второго – 0,9. Найти вероятность того, что взятая наудачу деталь из выбранного наудачу набора – стандартная.

Решение. Пусть событие – извлеченная деталь стандартна, событие – деталь извлечена из первого набора, событие – деталь извлечена из второго набора. Так как деталь вынимают из наугад выбранного набора, то события и равновозможные, и их вероятности .

Условная вероятность того, что из первого набора будет извлечена стандартная деталь . Условная вероятность того, что из второго набора будет извлечена стандартная деталь . Тогда искомая вероятность того, что взятая наудачу деталь из выбранного наудачу набора будет стандартной, по формуле полной вероятности равна

.

Формула Бейеса. Условная вероятность события в предположении, что событие уже произошло, определяют по формуле

( ).

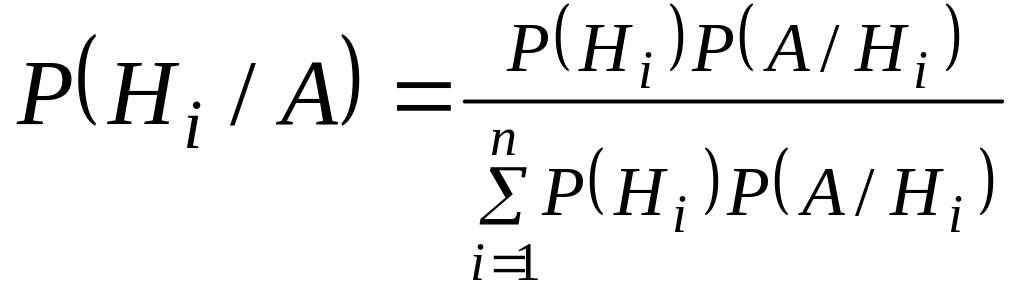Вероятности , вычисленные по формуле Бейеса, называют вероятностями гипотез.

Пример 7. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадет к первому контролеру, равна 0,6, а ко второму – 0,4. Вероятность того, что деталь будет признана стандартной первым контролером, равна 0,94, а вторым – 0,98. Деталь при проверке была признана стандартной. Найти вероятность того, что ее проверил первый контролер.

Решение. Обозначим через событие, состоящее в том, что деталь признана стандартной, гипотеза – деталь проверил первый контролер, гипотеза – деталь проверил второй контролер. По условию задачи имеем

(вероятность того, что деталь попадет к первому контролеру),

(вероятность того, что деталь попадет ко второму контролеру),

(вероятность того, что деталь будет признана стандартной первым контролером),

(вероятность того, что деталь будет признана стандартной вторым контролером).

Искомую вероятность того, что признанную стандартной деталь проверил первый контролер, найдем по формуле Бейеса:

.

До испытания вероятность гипотезы равнялась 0,6, а после того, как стал известен результат испытания, условная вероятность этой гипотезы изменилась и стала равной 0,59.