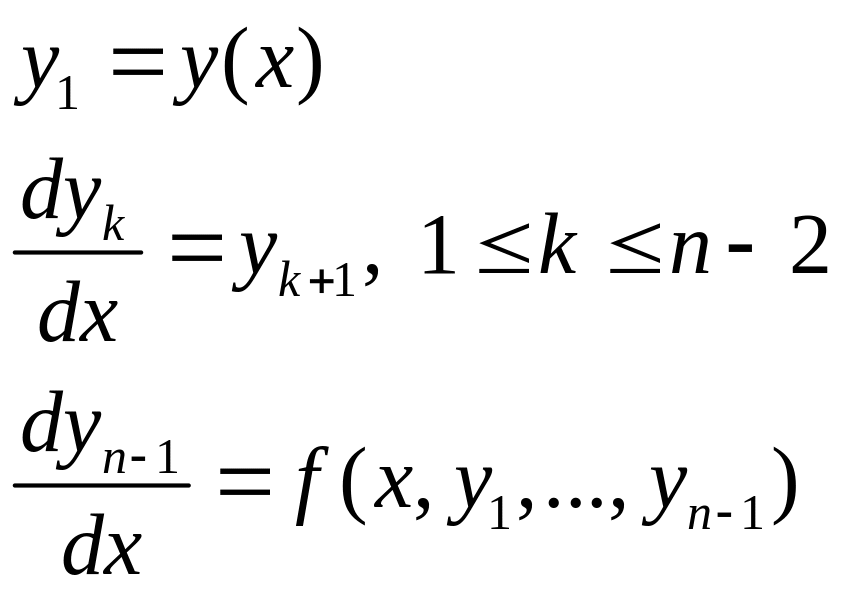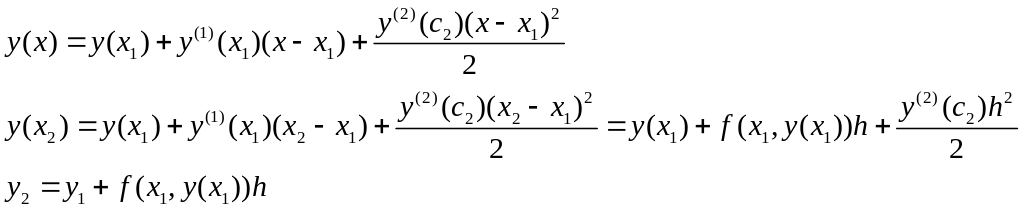Основные понятия и определения

Обыкновенными дифференциальными уравнениями (ДУ) называют уравнения, которые содержат одну или несколько производных от искомой функции . Общая форма записи ДУ:

(1.1)

Порядком ДУ называется порядок старшей производной, входящей в это уравнение.

Решением ДУ называется любая функция , которая при подстановке в уравнение (1.1) обращает его в тождество.

Процесс нахождения решения ДУ называется интегрированием ДУ.

Каждое ДУ имеет бесконечное множество решений, для нахождения частного решения требуется указать начальные условия. Если эти условия задаются при одном значении независимой переменной , то задача отыскания решения уравнения (1.1) называется задачей Коши.

Уравнение называется разрешенным относительно старшей производной, если его можно записать в виде:

(1.2)

Достаточно сложно в большинстве практических случаев отыскать аналитическое решение ДУ, выход – использование численных методов. Все численные методы разработаны для одного ДУ 1-го порядка, но легко распространяются на систему ДУ 1-го порядка. Конкретная прикладная задача может приводить к ДУ любого порядка, или к СДУ любого порядка, но известно, что обыкновенное ДУ -го порядка (1.2) можно свести к эквивалентной системе уравнений 1-го порядка при помощи замены :

(1.3)

Любой одношаговый метод имеет вид для некоторой функции , называемой функцией приращений, т. е. для получения решения в точке достаточно знать только его значение в точке . Поэтому, величину шага интегрирования можно менять в процессе решения.

1. Метод эйлера

Метод Эйлера хорошо демонстрирует подходы, используемые для разработки более точных и сложных методов. Его использование ограничено большой ошибкой численного решения, которая накапливается в процессе его применения. Тем не менее, он важен для изучения, т. к. анализ ошибки легче для понимания.

Зададим интервал , на котором необходимо получить решение уравнения с начальным условием . Разобьем отрезок на конечное число частей введением узловых точек , для простоты изложения и анализа будем предполагать, что узловые точки делят отрезок на равные части. Тогда , где и . Предположим, что функция имеет непрерывные производные до второго порядка включительно на , и применим разложение в ряд Тейлора.

(2.1)

где точка лежит между и .

После подстановки , и результирующее выражение примет вид:

(2.2)

Предположим, что вторая производная ограничена на отрезке интегрирования и шаг h достаточно мал, тогда в выражении (2.2) можно пренебречь вторым членом ряда Тейлора, получив выражение:

(2.3)

Полагаем , тогда

(2.4)

Повторение процесса дает последовательность точек, которые аппроксимируют интегральную кривую . Запишем общую формулу для шага, называемую формулой Эйлера:

, где

(2.3)

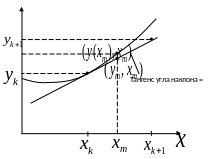
Геометрический смысл метода Эйлера заключается в аппроксимации решения на отрезке отрезком касательной, проведенной к графику решения в точке , т.е. вместо значения функции в точке получаем ординату касательной, проведенной к графику функции в точке (см. рис. 1).

Рис. 1. Геометрическая иллюстрация метода Эйлера